Přechod na menu, Přechod na obsah, Přechod na patičku
     

Podmíněná pravděpodobnost a nezávislost


nahoru

1. Motivační příklad

Mějme urnu s $a$ černými a $b$ bílými koulemi. Dvakrát táhneme bez vracení po jedné kouli.

Zajímá nás pravděpodobnost, s jakou ve druhém tahu vytáhneme bílou kouli, za předpokladu, že také v prvním tahu jsme vytáhli bílou kouli.

Nejprve označme náhodné jevy $B_1\ldots$ v 1. tahu jsme vytáhli bílou kouli
$B_2\ldots$ v 2. tahu jsme vytáhli bílou kouli

Z klasické definice pravděpodobnosti plyne, že $ P(B_1)=\frac{b}{a+b} $. Obdobně, v situaci, kdy jsme už vytáhli v 1. tahu bílou kouli, další bílou kouli vytáhneme s pravděpodobností

$$ P(B_2|B_1)=\frac{b-1}{a+b-1}, $$

protože pro 2. tah je k dispozici pouze $b-1$ bílých a $a$ černých koulí.

Označení $P(B_2|B_1)$ jsme použili pro podmíněnou pravděpodobnost náhodného jevu $B_2$ za podmínky výskytu náhodného jevu $B_1$.

Kromě toho je pravděpodobnost průniku náhodných jevů $B_1\cap B_2$ rovna

$$ P(B_1\cap B_2)=\frac{b}{a+b}\;\cdot\;\frac{b-1}{a+b-1}, $$

neboť příznivých jevů je $b(b-1)$ a všech možných výsledků dvou tahů je:

$1$ $2$ $\cdots$ $b-1$ $1$ $\cdots$ $a$
$1$ $\left(b_{i_1},b_{i_2}\right)$ $\left(b_{i_1},b_{i_3}\right)$ $\cdots$ $\left(b_{i_1},b_{i_b}\right)$ $\left(b_{i_2},c_{j_1}\right)$ $\cdots$ $\left(b_{i_1},c_{j_a}\right)$
$2$ $\left(b_{i_2},b_{i_1}\right)$ $\left(b_{i_2},b_{i_3}\right)$ $\cdots$ $\left(b_{i_2},b_{i_b}\right)$ $\left(b_{i_2},c_{j_1}\right)$ $\cdots$ $\left(b_{i_2},c_{j_a}\right)$
$\vdots$ $\vdots$ $\vdots$ $\vdots$ $\vdots$ jev $B_1$
$b$ $\left(b_{i_b},b_{i_1}\right)$ $\left(b_{i_b},b_{i_2}\right)$ $\cdots$ $\left(b_{i_b}\!,\!b_{i_{b\!-\!1}}\right)$ $\left(b_{i_b},c_{j_1}\right)$ $\cdots$ $\left(b_{i_b},c_{j_a}\right)$
$1$ $\left(c_{j_1},b_{i_1}\right)$ $\left(c_{j_1},b_{i_2}\right)$ $\cdots$ $\left(c_{j_1},b_{i_b}\right)$ $\left(c_{j_1},c_{j_2}\right)$ $\cdots$ $\left(c_{j_1},c_{j_a}\right)$
$\vdots$ $\vdots$ $\vdots$ $\vdots$ $\vdots$
$a$ $\left(c_{j_a},b_{i_1}\right)$ $\left(c_{j_a},b_{i_2}\right)$ $\cdots$ $\left(c_{j_a},b_{i_b}\right)$ $\left(c_{j_a},c_{j_1}\right)$ $\cdots$ $\left(c_{j_a}\!,\!c_{j_{a\!-\!1}}\right)$
$1$ $2$ $\cdots$ $b$ $1$ $\cdots$ $a-1$
jev $B_2$

takže všech možných jevů je

$$ b(b-1+a)+a(b+a-1)=b^2-b+ba+ab+a^2-a=(a+b)(a+b-1). $$

Podmíněnou pravděpodobnost lze zapsat i takto

\[ P(B_2|B_1)=\frac{P(B_1\cap B_2)}{P(B_1)} =\frac{\frac{b}{a+b}\;\cdot\;\frac{b-1}{a+b-1}}{\frac{b}{a+b}}=\frac{b-1}{a+b-1} \]

Tedy z $\Omega$ jsme přešli na $B_1$ a z náhodného jevu $B_2$ bereme jen ty, které jsou také v $B_1$.

nahoru

2. Definice a vlastnosti podmíněné pravděpodobnosti

Definice 2.1. Nechť $(\Omega,\mathcal{A},P)$ je pravděpodobnostní prostor, $B\in\mathcal{A}$, $P(B)\gt 0$. Pak číslo $$ P(A|B)=\frac{P(A\cap B)}{P(B)} $$ nazýváme podmíněnou pravděpodobností jevu $A$ za podmínky (že nastal jev) $B$.
Poznámka 2.2. Z předchozí definice ihned vyplývá, že pravděpodobnost průniku náhodných jevů lze vyjádřit $P(A\cap B)=P(A|B)P(B)$ a přitom se předpokládá, že $P(B)\gt 0$. Ukážeme, že tento vztah platí i v případě, že $P(B)=0$.

Nejprve je třeba si uvědomit, že $A\cap B \subseteq B$. Je-li tedy $P(B)=0$, pak $P(A\cap B)=0$.

Zcela symetricky platí také $P(A\cap B)=P(B|A)P(A)$.

Značení: Mějme pevně daný náhodný jev $B\in\mathcal{A}$, pro který platí $P(B)\gt 0$. Označme $$P_B:\;\mathcal{A}\to\langle0,1\rangle:\; P_B(A)=P(A|B)$$
Věta 2.3. $P_B$ je pravděpodobnost na $(\Omega,\mathcal{A})$ pro každé $B\in\mathcal{A}$, pro které $P(B)\gt 0$.
Důkaz.
Je-li $P_B$ je pravděpodobnost na $(\Omega,\mathcal{A})$, musí být normovaná, nezáporná a $\sigma$-aditivní.
(1) Normovanost $P_B(\Omega)=\frac{P(B\cap \Omega)}{P(B)}=\frac{P(B)}{P(B)}=1$.
(2) Nezápornost $P_B(A)=\frac{P(A\cap B)}{P(B)}\geq 0$ pro $\forall\;A\in\mathcal{A}$.
(3) $\sigma$-aditivita $\left\{A_n \right\}_{n=1}^\infty$ je posloupnost po dvou neslučitelných náhodných jevů
$\begin{array}{@{}l@{}c@{}l@{}} P_B\left( \bigcup\limits_{n=1}^\infty A_n\right) & = & \frac{P\left(\left( \bigcup\limits_{n=1}^\infty A_n\right)\cap B\right)}{P(B)}= \frac{P\left( \bigcup\limits_{n=1}^\infty (A_n\cap B)\right)}{P(B)}= \frac{\sum\limits_{n=1}^\infty P(A_n\cap B)}{P(B)}\\ &=& \sum\limits_{n=1}^\infty P(A_n|B)= \sum\limits_{n=1}^\infty P_B(A_n) \end{array}$
\(\Box\)
Věta 2.4. Platí
  1. $P(A|\Omega)=P(A)$ pro $\forall\;A\in\mathcal{A}$.
  2. $P\left( \bigcap\limits_{i=1}^n A_i\right)= P(A_1)\cdot P(A_2|A_1)\cdot P(A_3|A_1\cap A_2)\cdot \;\cdots\; \cdot P(A_n|A_1\cap\ldots\cap A_{n-1})$ pro $P\left( \bigcap\limits_{i=1}^{n-1} A_i\right)\gt 0$ (Věta o násobení pravděpodobností)
Důkaz.
  1. $P(A|\Omega)=\frac{P(A\cap\Omega)}{P(\Omega)}=\frac{P(A)}{P(\Omega)}=P(A)$ pro $\forall\;A\in\mathcal{A}$.
  2. $\begin{array}[t]{@{}l@{}c@{}l@{}} P\left( \bigcap\limits_{i=1}^n A_i\right) &=& P\left(A_n \cap \left(\bigcap\limits_{i=1}^{n-1} A_i\right) \right) \stackrel{pozn.2.2}{=} P\left(A_n|\bigcap\limits_{i=1}^{n-1} A_i\right) \underbrace{P\left( \bigcap\limits_{i=1}^{n-1} A_i\right)}_{pozn.2.2}\\ &=& P\left(A_n|\bigcap\limits_{i=1}^{n-1} A_i\right) P\left(A_{n-1}|\bigcap\limits_{i=1}^{n-2} A_i\right) \underbrace{P\left( \bigcap\limits_{i=1}^{n-2} A_i\right)}_{pozn.2.2}=\cdots\\ &=& P\left(A_n|\bigcap\limits_{i=1}^{n-1} A_i\right) P\left(A_{n-1}|\bigcap\limits_{i=1}^{n-2} A_i\right) \cdot \;\cdots\; \cdot P(A_2|A_1)\cdot P(A_1) \end{array}$
\(\Box\)
Definice 2.5. Nechť $(\Omega,\mathcal{A},P)$ je pravděpodobnostní prostor. Náhodné jevy $\left\{A_n \right\}_{n=1}^\infty \in \mathcal{A}$ tvoří úplný systém jevů na $(\Omega,\mathcal{A},P)$, jestliže platí \[ A_i\cap A_j = \emptyset,\ \text{pro }i\neq j,\ \text{a } \bigcup_{n=1}^\infty A_n=\Omega. \]
Věta 2.6. (Vzorec pro úplnou pravděpodobnost). Nechť posloupnost $\left\{A_n \right\}_{n=1}^\infty$ tvoří úplný systém jevů na $(\Omega,\mathcal{A},P)$ takový, že $P(A_i)\gt 0$ pro $i=1,2,\ldots$. Pak platí $$ P(B)=\sum\limits_{i=1}^\infty P(A_i)P(B|A_i). $$
Důkaz.
$P(B)$ $ = P(B\cap\Omega)=P\left(B\cap\bigcup\limits_{i=1}^\infty A_i \right) =P\left(\bigcup\limits_{i=1}^\infty(B\cap A_i) \right)$
$= \sum\limits_{i=1}^\infty P(B\cap A_i) \stackrel{pozn.2.2}{=}\sum\limits_{i=1}^\infty P(A_i)P(B|A_i)$
\(\Box\)
Věta 2.7. (Bayesův vzorec). Nechť posloupnost $\left\{A_n \right\}_{n=1}^\infty$ tvoří úplný systém jevů na $(\Omega,\mathcal{A},P)$ takový, že $P(A_i)\gt 0$ pro $i=1,2,\ldots$ a $B\in\mathcal{A}$, kde $P(B)\gt 0$. Pak \[ P(A_j|B)=\frac{P(A_j)P(B|A_j)}{\sum\limits_{i=1}^nP(A_i)P(B|A_i)} \quad\mbox{ pro }\quad j=1,2,\ldots . \]
Důkaz.
S využitím poznámky 2.2 a vzorce pro úplnou pravděpodobnost můžeme upravovat $$ P(A_j|B)= \frac{P(A_j\cap B)}{P(B)}= \frac{\overbrace{P(A_j)P(B|A_j)}^{pozn.2.2}} {\underbrace{\sum\limits_{i=1}^\infty P(A_i)P(B|A_i)}_{\text{úpl.pst}(V2.6)}}. $$
\(\Box\)
Věta 2.8. (Bayesův vzorec - modifikace) Nechť posloupnost $\left\{A_n \right\}_{n=1}^\infty$ tvoří úplný systém jevů na $(\Omega,\mathcal{A},P)$ takový, že $P(A_i)\gt 0$ pro $i=1,2,\ldots$, $A\in\mathcal{A}$, kde $P(A)\gt 0$ a $B\in\mathcal{A}$. Pak \[ P(B|A)=\frac{\sum\limits_{\{i:P(A\cap A_i)>0\}}P(A_i)P(A|A_i)P(B|A\cap A_i)}{\sum\limits_{i=1}^\infty P(A_i)P(A|A_i)}. \]
Důkaz.
Využitím předchozích vztahů lze lehce dospět k tvrzení (zkuste jako domácí cvičení).
\(\Box\)
Terminologie: $A_j$ $\cdots$ hypotézy, $j=1,2,\ldots$
$P(A_j)$ $\cdots$ apriorní pravděpodobnost
$P(A_j|B)$ $\cdots$ aposteriorní pravděpodobnost
Poznámka 2.9. Bayesův vzorec se používá v případě, jestliže:
  • Máme úplný systém hypotéz $A_1,\ldots,A_n$, které se navzájem vylučují a vyčerpávají všechny možnosti.
  • Přitom známe jejich apriorní pravděpodobnosti $P(A_i)$.
  • Nastal jev $B$ a navíc známe podmíněné pravděpodobnosti $P(B|A_i)$.
  • Co nás především zajímá, jsou nové aposteriorní pravděpodobnosti $P(A_i|B)$, které berou v úvahu, že nastal jev $B$.
Příklad 2.10. (Lékařská diagnostika) Je známo, že nějakou konkrétní nemocí, označme ji $\mathcal{D}$ (disease), trpí 1% populace. Nemoc je diagnostikována na základě vyšetření, jehož spolehlivost je 95%, jestliže vyšetřovaná osoba trpí nemocí $\mathcal{D}$, a je 70%, pokud nemocí $\mathcal{D}$ netrpí. Vyšetřujeme náhodně zvolenou osobu.
Určete pravděpodobnost správné diagnózy, pokud byl výsledek (a) pozitivní,
(b) negativní.
Řešení: Označme jev $A$ vyšetřované osoba trpí chorobou $\mathcal{D}$
jev $B$ & výsledek vyšetření je pozitivní
Ze zadání známe: apriorní pravděpodobnost $P(A)=0.01$, což je pravděpodobnost, že náhodně vybraná osoba má danou nemoc $\mathcal{D}$, říká se jí prevalence nemoci.
Spolehlivost vyšetření se popisuje pomocí dvou charakteristik:
  • pro pozitivní výsledek $P(B|A)=0.95$ tzv. senzitivita testu
  • pro negativní výsledek $P(\bar{B}|\bar{A})=0.7\;\;$ tzv. specificita testu
  1. Určíme aposteriorní pravděpodobnost správné diagnózy, pokud byl výsledek pozitivní, tj. spočítáme podmíněnou pravděpodobnost $P(A|B) = \frac{P(A\cap B)}{P(B)}$. Nejprve vypočítáme $\begin{array}{@{}l@{}c@{}l@{}} {P(B)} & = & P(B\cap\Omega)=P(B\cap(A\cup\bar{A})) =P(\underbrace{(B\cap A)\cup(B\cap \bar{A})}_{\scriptsize neslučitelné jevy})\\ &=&P(\underbrace{B\cap A}_{pozn.2.2})+ P(\underbrace{B\cap \bar{A}}_{pozn.2.2})\\ &=& P(A)P(B|A)+P(\bar{A})P(B|\bar{A})\\ &=& 0.01\cdot0.95+(1-0.01)\cdot(1-0.7) =\underbrace{0.0095}_{=P(A\cap B)}+\underbrace{0.297}_{=P(\bar{A}\cap B)}={0.3065} \end{array}$ Nakonec dosadíme $P(A|B) = \frac{P(A\cap B)}{P(B)}=\frac{P(A)P(B|A)}{P(B)} =\frac{0.0095}{0.3065}={0.030995}$ tj. $3.1$%, což je překvapivý výsledek, čekali jsme o mnoho lepší. Většina lidí bez zaváhání odpoví, že by mělo být $95$%, neboť taková je přece spolehlivost vyšetření pro pozitivního jedince.

    Vysvětleme si podrobně, co značí aposteriorní pravděpodobnost správného určení diagnózy, když výsledek testu byl pozitivní.

    Je třeba si uvědomit, že uvažujeme náhodně vybraného jedince. Pravděpodobnost, že má danou chorobu, je dána prevalencí, a ta činí 1%. Naproti tomu 99% nemocí netrpí. Mezi těmi, kteří nemocí trpí, dává test s 95% správný (tj. pozitivní) výsledek, (senzitivita testu). Mezi těmi, kteří nemocí netrpí, dává test s 70% správný (tj. negativní) výsledek (specificita testu), takže pozitivní (nesprávný) výsledek s 30%.

  2. Naprosto analogicky dostaneme $ \begin{array}{l@{}c@{}l} {P(\bar{A}|\bar{B})} &=& \dfrac{P(\bar{A}\cap \bar{B})}{P(\bar{B})} =\dfrac{P(\bar{A})P(\bar{B}|\bar{A})}{P(\bar{A})P(\bar{B}|\bar{A})+P({A})P(\bar{B}|{A})}\\ &=&\dfrac{(1-0.01)\cdot 0.7}{(1-0.01)\cdot 0.7+0.01\cdot(1-0.95)}\\ &=&\dfrac{0.693}{0.693+0.0005} = \dfrac{0.693}{0.6935}={0.99928}. \end{array} $
Na konkrétním příkladu s 100 000 jedinci si ukážeme, proč vyšla pravděpodobnost správného výsledku při pozitivním testu tak malá a pravděpodobnost správného výsledku při negativním testu tak vysoká.
$A\ \ldots\ $ nemoc má prevalence$=0.01$ $\bar{A}\ \ldots\ $ nemoc nemá celkem
1000 99 000 100 000
$B\ \ldots\ $test je pozitivní senzitivita$=0.95$
950		  
29 700		 30 650 $\begin{array}{@{}l@{}c@{}l} P(A|B) &=& \frac{950}{30\;650}\\ &=& 0.030995 \end{array} $
$\bar{B}\ \ldots\ $test je negativní  
50		 specificita$=0.7$
69 300		 69 350 $\begin{array}{@{}l@{}c@{}l} P(\bar{A}|\bar{B}) &=& \frac{69\;300}{69\;350}\\ &=& 0.99928 \end{array}$
nahoru

3. Nezávislost náhodných jevů

Velmi důležitým pojmem je nezávislost. Intuitivně cítíme, že jevy $A$ a $B$ jsou nezávislé, pokud hodnota pravděpodobnosti podmíněného jevu bude rovna nepodmíněné pravděpodobnosti, tj.

$$P(A|B) =\frac{P(A\cap B)}{P(B)}= P(A)\ \text{a}\ P(B|A) =\frac{P(A\cap B)}{P(A)}= P(B).$$

Odtud pak vychází následující definice nezávislosti.

Definice 3.1. Nechť $(\Omega,\mathcal{A},P)$ je pravděpodobnostní prostor. Pak řekneme, že jev $A\in\mathcal{A}$ a jev $B\in\mathcal{A}$ jsou nezávislé (vzhledem k pravděpodobnosti $P$), jestliže \[ P(A\cap B)=P(A)P(B). \]
Věta 3.2.
  1. Libovolný náhodný jev $A\in\mathcal{A}$ a jev jistý jsou nezávislé.
  2. Libovolný náhodný jev $A\in\mathcal{A}$ a jev nemožný jsou nezávislé.
  3. Nechť $A\in\mathcal{A}$ a $B\in\mathcal{A}$ jsou nezávislé jevy. Pak také $A$ a $\bar{B}$, $\bar{A}$ a ${B}$, $\bar{A}$ a $\bar{B}$ jsou nezávislé.
Důkaz.
  1. $P(\Omega)=1\;\wedge\; P(A\cap\Omega)=P(A)=P(A)\cdot 1=P(A)\cdot P(\Omega)$
  2. $P(\emptyset)=0\;\wedge\; P(A\cap\emptyset)=P(\emptyset)=0=P(A)\cdot P(\emptyset)$
  3. Nechť $A,B\in\mathcal{A}\;\wedge\;P(A\cap B)=P(A)P(B)$, počítejme \begin{align*} {P(A\cap\bar{B})} & = P(A\cap(\Omega-B))=P((A\cap\Omega)-(A\cap B))=P(A-\underbrace{(A\cap B)}_{\subseteq A})\\ &=P(A)-P(A\cap B)=P(A)-P(A)P(B)=P(A)(1-P(B))\\ &={P(A)P(\bar{B})} \end{align*} Analogicky dokážeme i ostatní tvrzení.
\(\Box\)
Definice 3.3. (Skupinová (sdružená) nezávislost). Nechť $(\Omega,\mathcal{A},P)$ je pravděpodobnostní prostor a $A_1,\ldots,A_n\in\mathcal{A}$. Řekneme, že náhodné jevy $A_1,\ldots,A_n$ jsou skupinově (sdruženě) nezávislé, jestliže pro libovolné $k\in\{1,\ldots,n\}$ a libovolnou množinu indexů $\{i_1,\ldots,i_k\}\subseteq \{1,\ldots,n\}$ platí $$ P\left(\bigcap\limits_{j=1}^k A_{i_j} \right)=\prod\limits_{j=1}^k P(A_{i_j}) $$ Nechť $M=\{A_i\in\mathcal{A},i\in\mathcal{J}\}$, kde $\mathcal{J}$ je daná indexová množina (i nekonečná). Řekneme, že náhodné jevy systému $M$ jsou nezávislé, jestliže pro každou konečnou množinu indexů $\{i_1,\ldots,i_n\}$, kde $i_j\in\mathcal{J},j=1,\ldots,n$ platí $$ P\left(\bigcap\limits_{j=1}^n A_{i_j} \right)=\prod\limits_{j=1}^n P(A_{i_j}) $$
Příklad 3.4. Dvakrát házíme kostkou.
Uvažujme následující jevy $A$ v 1. hodu padne sudé číslo
$B$ v 2. hodu padne liché číslo
$C$ v obou hodech padne číslo stejné parity

Protože platí

$\begin{array}{@{}lcl@{$\qquad\qquad$}lcl@{}} P(A) &=& \frac{3\cdot 6}{36}=\frac{1}{2} & P(A\cap B) &=& \frac{3\cdot 3}{36}=\frac{1}{4}=P(A)P(B)\\[1ex] P(B) &=& \frac{6\cdot 3}{36}=\frac{1}{2} & P(A\cap C) &=& \frac{3\cdot 3}{36}=\frac{1}{4}=P(A)P(C)\\[1ex] P(C) &=& \frac{3\cdot 3+3\cdot 3}{36}=\frac{1}{2} & P(A\cap B\cap C) &=& \frac{0}{36}=0\neq P(A)P(B)P(C) \end{array}$

jsou jevy $A$, $B$ a $C$ po dvou nezávislé, ale ne skupinově nezávislé.

Poznámka 3.5. Zřejmě platí: jsou-li jevy $A_1,\ldots,A_n$ nezávislé, jsou i skupinově nezávislé.
Věta 3.6.
  1. Libovolná podmnožina skupinově nezávislých náhodných jevů je množinou nezávislých náhodných jevů.
  2. Jestliže v dané množině nezávislých náhodných jevů nahradíme libovolný počet jevů jevy opačnými, opět dostaneme množinu nezávislých náhodných jevů.
  3. Jestliže $A_1,\ldots,A_n$ jsou nezávislé náhodné jevy, pak $$ P\left(\bigcup\limits_{i=1}^n A_{i} \right)= 1-\prod\limits_{i=1}^n \left(1-P(A_{i})\right). $$
Důkaz.

$(a)$ i $(b)$ zřejmé.

$(c)$ $P\left(\bigcup\limits_{i=1}^n A_{i} \right)= P\left(\overline{\bigcap\limits_{i=1}^n \bar{A}_{i}} \right) =1-P\left(\bigcap\limits_{i=1}^n \bar{A}_{i} \right) =1-\prod\limits_{i=1}^n P(\bar{A}_{i}) =1-\prod\limits_{i=1}^n \left(1-P(A_{i})\right).$
\(\Box\)
Věta 3.7. (Borelovo lemma). Nechť $\left\{A_n \right\}_{n=1}^\infty$ jsou nezávislé jevy. Pak $ P\left(\!\limsup\limits_{n\to\infty}\! A_n\!\right) \!=\!0\vee 1$ podle toho, zda řada $\sum\limits_{n=1}^\infty P(A_n)$ konverguje nebo diverguje.
Důkaz.
  1. Jestliže řada $\sum\limits_{n=1}^\infty P(A_n)\lt\infty$ konverguje, pak podle Cantelliho lemmatu (V.7.4), které dokonce nepožaduje ani nezávislost náhodných jevů, platí $P\left(\limsup\limits_{n\to\infty} A_n\right)=0$.
  2. Nechť $\sum\limits_{n=1}^\infty P(A_n)=\infty$ diverguje. Protože $P\!\left(\!\limsup\limits_{n\to\infty}\!A_n\!\right)= P\!\left(\!\bigcap\limits_{n=1}^\infty \bigcup\limits_{k=n}^\infty A_k\!\right)$, označme nejprve $B_n=\bigcup\limits_{k=n}^\infty A_k\supseteq B_{n+1} =\bigcup\limits_{k=n+1}^\infty A_k$ a upravujme $$\begin{array}{@{}l@{}c@{}l@{}} {P\!\left(\!\limsup\limits_{n\to\infty}\!A_n\!\right)} &=& P\!\left(\!\bigcap\limits_{n=1}^\infty \bigcup\limits_{k=n}^\infty A_k\!\right) =P\!\left(\!\bigcap\limits_{n=1}^\infty B_n\!\right) \stackrel{V7.2,(3)}{=} \lim\limits_{n\to\infty}P(B_n)\\ &=& \lim\limits_{n\to\infty}P\!\left(\! \bigcup\limits_{k=n}^\infty A_k\!\right) =\lim\limits_{n\to\infty}\lim\limits_{N\to\infty} P\!\left(\!\bigcup\limits_{k=n}^N A_k\!\right)\\ &=& \lim\limits_{n\to\infty}\lim\limits_{N\to\infty} P\!\left(\!\overline{\bigcap\limits_{k=n}^N \bar{A}_k}\!\right) =1\!-\!\lim\limits_{n\to\infty}\lim\limits_{N\to\infty} P\!\left(\!\bigcap\limits_{k=n}^N \bar{A}_k\!\right)\\ &=& 1\!\!-\!\!\lim\limits_{n\to\infty}\!\lim\limits_{N\to\infty}\! \prod\limits_{k=n}^N\!P(\bar{A}_k)\!=\! 1\!\!-\!\!\lim\limits_{n\to\infty}\!\lim\limits_{N\to\infty} \!\prod\limits_{k=n}^N\!(1\!\!-\!\!P(A_k))\\ &\geq& 1-\lim\limits_{n\to\infty}\lim\limits_{N\to\infty} \prod\limits_{k=n}^N e^{-P(A_k)}\\ &=&1-\lim\limits_{n\to\infty}\lim\limits_{N\to\infty} e^{-\sum\limits_{k=n}^NP(A_k)}=1-0= 1. \end{array}$$

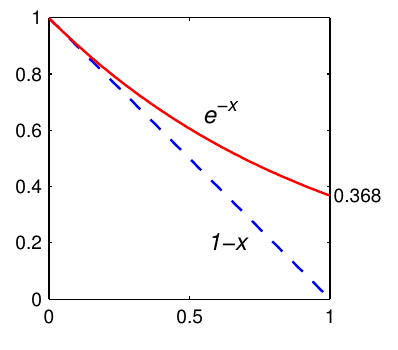
Pro $x\in(0,1)$ platí

$|\ln(1-x)|\geq x$, tj.

$\ln(1-x)\leq -x$

$1-x\leq e^{-x}$

Graf Borelovo lemma
\(\Box\)
RNDr. Marie Forbelská, Ph.D., Mgr. Jan Koláček, Ph.D. |
ÚMS, Přírodovědecká fakulta, Masarykova univerzita |
Návrat na úvodní stránku webu, přístupnost |
Stránky Přírodovědecké fakulty MU
| Technická spolupráce:
| Servisní středisko pro e-learning na MU
| Fakulta informatiky Masarykovy univerzity, 2013

Centrum interaktivních a multimediálních studijních opor pro inovaci výuky a efektivní učení | CZ.1.07/2.2.00/28.0041