2.2 Báze a jejich transformace

Bázi vektorového prostoru $V$ můžeme definovat jako množinu lineárně nezávislých vektorů, které tzv. generují vektorový prostor $V$, tj. kdy každý vektor z vektorového prostoru $V$ lze vyjádřit jako lineární kombinaci těchto (bázových) vektorů. Významnou roli při praktických výpočtech hrají báze ortogonální, resp. ortonormální. Ortogonální báze je speciálním případem obecné báze, kdy různé bázové vektory jsou na sebe kolmé. Pro bázové vektory $\vec{x}_i,\,\vec{x}_j,\,i\neq j$ tedy platí

$\vec{x}_i\cdot\vec{x}_j={x}_i{x}_j=0$, případně v algebraické notaci, $(\vec{x}_i,\vec{x}_j)=0$.

2.20

Ortonormální báze je speciálním případem ortogonální báze, kdy všechny bázové vektory (značíme je v tomto případě $\vec{e}_i$, často se také používá $\mathbf{\hat{x}}_i$) mají navíc jednotkovou velikost,

$ \vec{e}_i\cdot\vec{e}_j=\delta_{ij}$, případně, $(\vec{e}_i,\vec{e}_j)=\delta_{ij}$.

2.21

Na příkladu obrázku 2.1 zkonstruujeme matice přechodu mezi bázemi a ukážeme princip reprezentace vektoru v různých bázích v $\mathbb{R}^2$ (v případě vyšší dimenze vektorového prostoru bude postup zcela analogický).

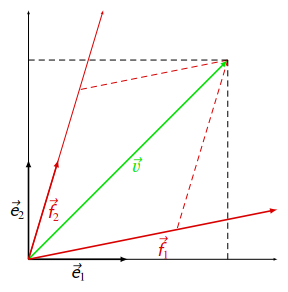
Obrázek 2.1: Schéma reprezentace vektoru $\vec{v}$, vyznačeného zelenou barvou, ve dvou různých bázích v $\mathbb{R}^2$, v černě vyznačené ortonormální bázi s bázovými vektory $\vec{e}_1,\,\vec{e}_2$ a v červeně vyznačené obecné bázi s bázovými vektory $\vec{f}_1,\,\vec{f}_2$. Přechod z černé do červené báze je dán vztahy: $\vec{f}_1=2,\!5\,\vec{e}_1+0,\!5\,\vec{e}_2$, $\vec{f}_2=0,\!3\,\vec{e}_1+\vec{e}_2$. V černě vyznačené bázi má vektor $\vec{v}$ složky o velikosti $(2,2)$, velikost složek je zde znázorněna průmětem vektoru $\vec{v}$ do směrů jednotlivých vektorů báze, zvýrazněným černými čárkovanými čarami a znamená poměr velikosti těchto průmětů ku velikosti příslušných bázových vektorů. Totéž platí v červeně vyznačené bázi, kde velikost složek je dána průmětem vektoru $\vec{v}$ do směrů jednotlivých bázových vektorů, zvýrazněným červenými čárkovanými čarami. Velikost složek vektoru $\vec{v}$ v červené bázi bude $\left(\dfrac{28}{47},\dfrac{80}{47}\right)\approx(0,\!6;\,1,\!7)$.

Jsou zavedeny dvě báze $\mathcal{E}$ a $\mathcal{F}$, černá a červená, s bázovými vektory $\vec{e}_1,\,\vec{e}_2$ a $\vec{f}_1,\,\vec{f}_2$, kdy černá báze je ortonormální, červená báze je zcela obecná. Přechod z černé báze $\mathcal{E}$ do červené báze $\mathcal{F}$ je zde dán vztahy (popisujícími vektorový součet)

$$ \begin{array}{l c r c r} \vec{f}_1=2,\!5\,\vec{e}_1+0,\!5\,\vec{e}_2,\\ \vec{f}_2=0,\!3\,\vec{e}_1+\vec{e}_2. \end{array} $$

2.22

Můžeme tedy ihned napsat matici přechodu $\mathbf{T}$ z báze $\mathcal{E}$ do báze $\mathcal{F}$:

$$ \mathbf{T}\,(\mathcal{E}\mapsto\mathcal{F}) = \left(\begin{array}{c} \dfrac{5}{2}&\dfrac{1}{2}\\[8pt]\dfrac{3}{10}&{1} \end{array}\right). $$

2.23

Matici přechodu (2.23, i všechny další) lze zapsat také pomocí sloupcového formalismu, tj. vektory $\vec{f}_1,\,\vec{f}_2$ budou zapsány jako sloupcové. V takovém případě bude sloupcově zapsaná matice přechodu násobit libovolný, rovněž sloupcový vektor (viz rovnice 2.29 v dalším výkladu), zapsaný za maticí. Ostatní dále popsané principy zůstanou nezměněné.

Z rovnic 2.22 snadno odvodíme rovnice pro $\vec{e}_1,\,\vec{e}_2$, tedy rovnice opačného přechodu z červené báze $\mathcal{F}$ do černé báze $\mathcal{E}$:

$$ \begin{array}{l c r c r} \vec{e}_1=&\dfrac{20}{47}\vec{f}_1&-\dfrac{10}{47}\vec{f}_2,\\ \vec{e}_2=&-\dfrac{6}{47}\vec{f}_1&+\dfrac{50}{47}\vec{f}_2. \end{array} $$

2.24

V maticovém zápisu půjde o zpětnou matici přechodu $\mathbf{S}$, která je inverzní vůči matici $\mathbf{T}$, tedy $\mathbf{S}=\mathbf{T}^{-1}$:

$$ \mathbf{S}\,(\mathcal{F}\mapsto\mathcal{E})= \left(\begin{array}{r} \dfrac{20}{47}&-\dfrac{10}{47}\\-\dfrac{6}{47}&\dfrac{50}{47} \end{array}\right). $$

2.25

Daný (zelený) vektor $\vec{v}$ má vodorovnou a svislou složku v černé bázi $\mathcal{E}$ znázorněnou průmětem vektoru do vodorovné a svislé osy, tj. do směrů, které odpovídají bázovým vektorům $\vec{e}_1,\,\vec{e}_2$. Velikosti těchto složek budou odpovídat poměru délek těchto průmětů (vyznačených čárkovaně černě) a příslušných bázových vektorů, můžeme tedy vektor $\vec{v}$ zapsat jako vektorový součet (v tomto případě předem zvolených) násobků vektorů báze $\mathcal{E}$, nebo pouze pomocí složek:

$ \vec{v}=2\,\vec{e}_1+2\,\vec{e}_2$, nebo $\vec{v}=(2,2), $

2.26

kdy ve druhém případě implicitně předpokládáme, že se pohybujeme v bázi $\mathcal{E}$. Určení složek vektoru $\vec{v}$ v červené bázi $\mathcal{F}$ bude zcela obdobné. Průměty vektoru $\vec{v}$ do směrů bázových vektorů $\vec{f}_1,\,\vec{f}_2$ jsou znázorněné čárkovaně červeně, velikosti složek budou opět odpovídat poměru délek těchto průmětů a příslušných bázových vektorů. Uvědomíme-li si, že vektor $\vec{v}$ je jen jeden, a tedy vektorový součet jeho složek musí být stejný bez ohledu na to ze které báze se na něj díváme, můžeme pro stanovení jeho složek v bázi $\mathcal{F}$ například nejprve analogicky k rovnici 2.26 obecně napsat

$$ \vec{v}=\text{a}\vec{f}_1+\text{b}\vec{f}_2=2\,\vec{e}_1+2\,\vec{e}_2. $$

2.27

Dosazením za vektory $\vec{e}_1,\,\vec{e}_2$ z rovnice 2.24 dopočítáme velikosti složek a, b:

$$ \vec{v}=\frac{28}{47}\vec{f}_1+\frac{80}{47}\vec{f}_2,\quad\text{nebo}\quad\vec{v}=\left(\frac{28}{47},\frac{80}{47}\right), $$

2.28

kdy ve druhém případě opět implicitně předpokládáme, že se pohybujeme v bázi $\mathcal{F}$. Stejný výsledek dostaneme, vynásobíme-li vektor $\vec{v}$, zapsaný pomocí jeho složek v černé bázi $\mathcal{E}$, maticí $\mathbf{S}$ přechodu z červené báze $\mathcal{F}$ do černé báze $\mathcal{E}$:

$$ (\text{a},\text{b})=(2,2) \left(\begin{array}{rrr} \dfrac{20}{47}&-\dfrac{10}{47}\\ -\dfrac{6}{47}&\dfrac{50}{47} \end{array}\right)=\left(\frac{28}{47},\frac{80}{47}\right). $$

2.29

Zpětnou transformaci můžeme ověřit vynásobením takto získaných složek $(\text{a},\text{b})$ vektoru $\vec{v}$ vbázi $\mathcal{F}$ maticí $\mathbf{T}$ přechodu z černé báze $\mathcal{E}$ do červené báze $\mathcal{F}$, výsledkem musí být původní složky vektoru $\vec{v}$ v bázi $\mathcal{E}$:

$$\left(\frac{28}{47},\frac{80}{47}\right) \left(\begin{array}{c} \dfrac{5}{2}&\dfrac{1}{2}\\ \dfrac{3}{10}&1 \end{array}\right)=(2,2). $$

2.30

V případě ortonormálních bází budou matice přechodu mezi nimi maticemi pouze rotačními, tedy ortogonálními. Musí tedy platit: $\mathbf{T}^{-1}=\mathbf{T}^{T}$ a zároveň: $\det\mathbf{T}=\det\mathbf{T}^{-1}=\pm 1$ (pokud $\det\mathbf{T}=\det\mathbf{T}^{-1}=-1$, jedná se o tzv. nepravou (nevlastní) rotaci, tedy rotaci spojenou se zrcadlením v rovině kolmé k ose rotace). Další podrobnosti, týkající se vektorového a maticového počtu včetně počítání s bázemi – viz příslušné kursy lineární algebry.

nahoru

Příklady

2.15

Nalezněte matice přechodu mezi standardní ortonormální bází (kartézské souřadnicové soustavy) a bází cylindrické souřadnicové soustavy.

$\left(\begin{array}{c} \hat{r}\\\hat{\phi}\\\hat{z}\end{array}\right)= \left(\begin{array}{c} \cos\phi&\sin\phi&0\\-\sin\phi&\cos\phi&0\\0&0&1\end{array}\right) \left(\begin{array}{c} \hat{x}\\\hat{y}\\\hat{z}\end{array}\right)$, $\left(\begin{array}{c} \hat{x}\\\hat{y}\\\hat{z}\end{array}\right)= \left(\begin{array}{c} \cos\phi&-\sin\phi&0\\\sin\phi&\cos\phi&0\\0&0&1\end{array}\right) \left(\begin{array}{c} \hat{r}\\\hat{\phi}\\\hat{z}\end{array}\right)$

2.16

Nalezněte matice přechodu mezi standardní ortonormální bází (kartézské souřadnicové soustavy) a bází sférické souřadnicové soustavy.

$\left(\begin{array} \hat{r}\\\hat{\theta}\\\hat{\phi}\end{array}\right)= \left(\begin{array}{r} \sin\theta\cos\phi&\sin\theta\sin\phi&\cos\theta\\ \cos\theta\cos\phi&\cos\theta\sin\phi&-\sin\theta\\ -\sin\phi&\cos\phi&0\end{array}\right) \left(\begin{array}{r} \hat{x}\\\hat{y}\\\hat{z}\end{array}\right)$,

$\left(\begin{array}{r}\hat{x}\\\hat{y}\\\hat{z}\end{array}\right)= \left(\begin{array}{r}\sin\theta\cos\phi&\cos\theta\cos\phi&-\sin\phi\\ \sin\theta\sin\phi&\cos\theta\sin\phi&\cos\phi\\ \cos\theta&-\sin\theta&0\end{array}\right) \left(\begin{array}{r}\hat{r}\\\hat{\phi}\\\hat{z}\end{array}\right)$

2.17

Nalezněte matici přechodu při otočení dvourozměrné kartézké souřadnicové soustavy o úhel $\alpha$ (tzv. matici rotace).

$\left(\begin{array}{r} x^\prime\\y^\prime\end{array}\right)=\left(\begin{array}{r}\cos\alpha&\sin\alpha\\-\sin\alpha&\cos\alpha\end{array}\right) \left(\begin{array}{r}x\\y\end{array}\right)$

2.18

Nalezněte matici $\mathbf{G}$ Galileovy transformace časoprostoru. Galileova časoprostorová transformace je daná přiřazením $(t,x,y,z)^T\mapsto(t^\prime,x^\prime,y^\prime,z^\prime)^T$ , kde $t^\prime=t$, $x^\prime=x−v_xt$, $y^\prime=y−v_yt$ a $z^\prime=z−v_zt$, přičemž vektor $\vec{v}=(v_x,v_y,v_z)$ interpretujeme jako rychlost.

$\left(\begin{array}{c} 1&0&0&0\\-v_x&1&0&0\\-v_y&0&1&0\\-v_z&0&0&1\end{array}\right)$

Vynásobením matic dokažte vztah $\mathbf{G}_{\mathbf{u}}\times\mathbf{G}_{\mathbf{v}}=\mathbf{G}_{\mathbf{u+v}}$ a vysvětlete, proč se tento vztah nazývá klasickým pravidlem skládání rychlostí.

$\left(\begin{array}{c} 1&0&0&0\\-v_x-u_x&1&0&0\\-v_y-u_y&0&1&0\\-v_z-u_z&0&0&1\end{array}\right)$

2.19

Vektor $\vec{a}$ má v ortonormální bázi $\mathcal{B}$ v $\mathbb{R}^2$ složky $\left(11/2,\,-1\right)$. Přechod mezi bázemi $\mathcal{B}$ a $\mathcal{B^\prime}$ je dán vztahy

$$ \begin{array}{l c r c r} \vec{e}_1^{\,\,\prime}&=&4\,\vec{e}_1&+&\vec{e}_2,\\ \vec{e}_2^{\,\,\prime}&=&\dfrac{3}{2}\vec{e}_1&-&2\,\vec{e}_2. \end{array} $$

Určete

matici $\mathbf{T}$ přechodu z báze $\mathcal{B}$ do báze $\mathcal{B^\prime}$,
$\mathbf{T}= \left(\begin{array}{r}4&1\\\dfrac{3}{2}&-2\\\end{array}\right)$
matici $\mathbf{S}$ přechodu z báze $\mathcal{B^\prime}$ do báze $\mathcal{B}$,
$\mathbf{S}=\left(\begin{array}{r}\dfrac{4}{19}&\dfrac{2}{19}\\[8pt]\dfrac{3}{19}&-\dfrac{8}{19}\\\end{array}\right)$
složky vektoru $\vec{a}$ v bázi $\mathcal{B^\prime}$.
$\vec{a}_{(\mathcal{B^\prime})}=(1,1)$

Je báze $\mathcal{B^\prime}$ ortonormální (uveďte důvod)?

Báze $\mathcal{B^\prime}$ není ortonormální.

Nakreslete obrázek, znázorňující velikost a směr všech uvedených vektorů, tj. vektorů obou bází i vektoru $\vec{a}$.

2.20

Vektor $\vec{a}$ má v ortonormální bázi $\mathcal{B}$ složky $(1,0,-2)$. Přechod mezi bázemi $\mathcal{B}$ a $\mathcal{B^\prime}$ je dán vztahy

$$\begin{array}{l c r c r c r} \vec{e}_1&=&-\vec{e}_1^{\,\,\prime}&+&\vec{e}_2^{\,\,\prime}&-&\vec{e}_3^{\,\,\prime},\\ \vec{e}_2&=&\vec{e}_1^{\,\,\prime} & & &+&2\,\vec{e}_3^{\,\,\prime},\\ \vec{e}_3&=&\vec{e}_1^{\,\,\prime} &+&\vec{e}_2^{\,\,\prime}&+&2\,\vec{e}_3^{\,\,\prime}. \end{array}$$

Určete

matici $\mathbf{T}$ přechodu z báze $\mathcal{B}$ do báze $\mathcal{B^\prime}$,
$\mathbf{T}= \left(\begin{array}{r}-2&-3&2\\0&-1&1\\1&2&-1\end{array}\right)$
matici $\mathbf{S}$ přechodu z báze $\mathcal{B^\prime}$ do báze $\mathcal{B}$,
$\mathbf{S}= \left(\begin{array}{r}-1&1&-1\\1&0&2\\1&1&2 \end{array}\right)$
složky vektoru $\vec{a}$ v bázi $\mathcal{B^\prime}$.
$\vec{a}_{(\mathcal{B^\prime})}=(-3,-1,-5)$

Je báze $\mathcal{B^\prime}$ ortonormální (uveďte důvod)?

Báze $\mathcal{B^\prime}$ není ortonormální.

2.21

Vektor $\vec{a}$ má v ortonormální bázi $\mathcal{B^\prime}$ složky $(1,2,-1)$. Přechod mezi bázemi $\mathcal{B}$ a $\mathcal{B^\prime}$ je dán vztahy

$$\begin{array}{l c r c r c r} \vec{e}_1&=& & &\vec{e}_2^{\,\,\prime}&-&\vec{e}_3^{\,\,\prime},\\ \vec{e}_2&=&\vec{e}_1^{\,\,\prime}& & &+&2\,\vec{e}_3^{\,\,\prime},\\ \vec{e}_3&=&\vec{e}_1^{\,\,\prime}&+&\vec{e}_2^{\,\,\prime}&+&2\,\vec{e}_3^{\,\,\prime}. \end{array} $$

Určete

matici $\mathbf{T}$ přechodu z báze $\mathcal{B}$ do báze $\mathcal{B^\prime}$,
$\mathbf{T}= \left(\begin{array}{r}2&3&-2\\0&-1&1\\-1&-1&1\end{array}\right)$
matici $\mathbf{S}$ přechodu z báze $\mathcal{B^\prime}$ do báze $\mathcal{B}$,
$\mathbf{S}= \left(\begin{array}{r}0&1&-1\\1&0&2\\1&1&2 \end{array}\right)$
složky vektoru $\vec{a}$ v bázi $\mathcal{B}$.
$\vec{a}_{(\mathcal{B})}=(3,2,-1)$

Je báze $\mathcal{B^\prime}$ ortonormální (uveďte důvod)?

Báze $\mathcal{B^\prime}$ není ortonormální.

2.22

Vektor $\vec{a}$ má v ortonormální bázi $\mathcal{B^\prime}$ složky $(1,2,-1)$. Přechod mezi bázemi $\mathcal{B}$ a $\mathcal{B^\prime}$ je dán vztahy

$$\begin{array}{l c r c r c r} \vec{e}_1&=&\vec{e}_1^{\,\,\prime} &-&2\,\vec{e}_2^{\,\,\prime}&-&3\,\vec{e}_3^{\,\,\prime},\\ \vec{e}_2&=&2\,\vec{e}_1^{\,\,\prime}&-&\vec{e}_2^{\,\,\prime} &-&\vec{e}_3^{\,\,\prime},\\ \vec{e}_3&=&\vec{e}_1^{\,\,\prime} &+&\vec{e}_2^{\,\,\prime} &+&\vec{e}_3^{\,\,\prime}. \end{array} $$

Určete

matici $\mathbf{T}$ přechodu z báze $\mathcal{B}$ do báze $\mathcal{B^\prime}$,
$\mathbf{T}= \left(\begin{array}{r}0&1&1\\1&2&5\\-1&-1&-3\end{array}\right)$
matici $\mathbf{S}$ přechodu z báze $\mathcal{B^\prime}$ do báze $\mathcal{B}$,
$\mathbf{S}= \left(\begin{array}{r}1&-2&-3\\2&-1&-1\\-1&1&1\end{array}\right)$
složky vektoru $\vec{a}$ v bázi $\mathcal{B}$.
$\vec{a}_{(\mathcal{B})}=(0,2,3)$

Je báze $\mathcal{B^\prime}$ ortonormální (uveďte důvod)?

Báze $\mathcal{B^\prime}$ není ortonormální.

2.23

Vektor $\vec{a}$ má ve standardní kartézské bázi $\mathcal{E}$ složky $(1,-\sqrt{3},1)$. Dále jsou zadány dvě báze $\mathcal{B}$ a $\mathcal{B^\prime}$, přičemž matice $\mathbf{R}$ přechodu z báze $\mathcal{E}$ do báze $\mathcal{B^\prime}$ má tvar

$$\mathbf{R}(\mathcal{E}\longmapsto\mathcal{B^\prime})= \left(\begin{array}{r} \frac{\sqrt{3}}{2}&\frac{1}{2}&0\\[2pt]-\frac{1}{2}&\frac{\sqrt{3}}{2}&0\\[2pt]0&0&1 \end{array}\right).$$

Přechod mezi bázemi $\mathcal{B}$ a $\mathcal{B^\prime}$ je dán vztahy

$$\begin{array}{l c r c r c r} \vec{e}_1&=&\vec{e}_1^{\,\,\prime} &-&2\,\vec{e}_2^{\,\,\prime}&-&2\,\vec{e}_3^{\,\,\prime},\\ \vec{e}_2&=&2\,\vec{e}_1^{\,\,\prime}&-&2\,\vec{e}_2^{\,\,\prime}&+& \vec{e}_3^{\,\,\prime},\\ \vec{e}_3&=&-\vec{e}_1^{\,\,\prime} &+&2\,\vec{e}_2^{\,\,\prime}&+&3\,\vec{e}_3^{\,\,\prime}. \end{array} $$

Určete

matici $\mathbf{T}$ přechodu z báze $\mathcal{B}$ do báze $\mathcal{B^\prime}$,
$\mathbf{T}= \left(\begin{array}{r}-4&1&-3\\-7&1&-5\\1&0&1\end{array}\right)$
matici $\mathbf{S}$ přechodu z báze $\mathcal{B^\prime}$ do báze $\mathcal{B}$,
$\mathbf{S}= \left(\begin{array}{r}1&-1&-2\\2&-1&1\\-1&1&3\end{array}\right)$
složky vektoru $\vec{a}$ v bázích $\mathcal{B}$ a $\mathcal{B^\prime}$.
$\vec{a}_{(\mathcal{B^\prime})}=(0,-2,1)$, $\vec{a}_{(\mathcal{B})}=(15,-2,11)$,}}

Jsou báze $\mathcal{B}$ a $\mathcal{B^\prime}$ ortonormální (uveďte důvod)?

$\mathcal{B^\prime}$ ano, $\mathcal{B}$ ne.

2.24

Vektor $\vec{a}$ má ve standardní kartézské bázi $\mathcal{E}$ složky $(1,1,1)$. Dále jsou zadány dvě báze $\mathcal{B}$ a $\mathcal{B^\prime}$, přičemž matice $\mathbf{R}$ přechodu z báze $\mathcal{E}$ do báze $\mathcal{B^\prime}$ má tvar

$$\mathbf{R}(\mathcal{E}\longmapsto\mathcal{B^\prime})= \left(\begin{array}{r} \frac{1}{2}&0&\frac{1}{2}\\0&1&0\\-1&0&1 \end{array}\right).$$

Přechod mezi bázemi $\mathcal{B}$ a $\mathcal{B^\prime}$ je dán vztahy

$$\begin{array}{l c r c r c r} \vec{e}_1&=& & &\vec{e}_2^{\,\,\prime}&+&\vec{e}_3^{\,\,\prime},\\ \vec{e}_2&=&2\,\vec{e}_1^{\,\,\prime}& & &+&\vec{e}_3^{\,\,\prime},\\ \vec{e}_3&=&-\vec{e}_1^{\,\,\prime} &+&\vec{e}_2^{\,\,\prime}& & \end{array} $$

Určete

matici $\mathbf{R}^{-1}$ přechodu z báze $\mathcal{B^\prime}$ do báze $\mathcal{E}$,
$\mathbf{R}^{-1}= \left(\begin{array}{r}1&0&-\frac{1}{2}\\0&1&0\\1&0&\frac{1}{2}\end{array}\right)$
matici $\mathbf{T}$ přechodu z báze $\mathcal{E}$ do báze $\mathcal{B}$,
$\mathbf{T}= \left(\begin{array}{r}-1&1&1\\0&0&2\\-\frac{1}{2}&1&-\frac{1}{2}\end{array}\right)$
matici $\mathbf{S}$ přechodu z báze $\mathcal{B}$ do báze $\mathcal{E}$
$\mathbf{S}= \left(\begin{array}{r}-2&\frac{3}{2}&2\\-1&1&2\\0&\frac{1}{2}&0\end{array}\right)$
složky vektoru $\vec{a}$ v bázích $\mathcal{B}$ a $\mathcal{B^\prime}$.
$\vec{a}_{(\mathcal{B^\prime})}=(2,1,0)$, $\vec{a}_{(\mathcal{B})}=(-3,3,4)$

Jsou báze $\mathcal{B}$ a $\mathcal{B^\prime}$ ortonormální (uveďte důvod)?

$\mathcal{B^\prime}$ ne, $\mathcal{B}$ ne.

2.25

$$\mathbf{R}(\mathcal{E}\longmapsto\mathcal{B^\prime})= \left(\begin{array}{r} 0&-1&0\\1&0&0\\0&0&-1 \end{array}\right).$$

Přechod mezi bázemi $\mathcal{B}$ a $\mathcal{B^\prime}$ je dán vztahy

Určete

matici $\mathbf{T}$ přechodu z báze $\mathcal{E}$ do báze $\mathcal{B}$,
$\mathbf{T}= \left(\begin{array}{r}1&0&-1\\0&-2&-1\\1&1&0\end{array}\right)$
matici $\mathbf{S}$ přechodu z báze $\mathcal{B}$ do báze $\mathcal{E}$,
$\mathbf{S}= \left(\begin{array}{r}-1&1&2\\1&-1&-1\\-2&1&2\end{array}\right)$
složky vektoru $\vec{a}$ v bázích $\mathcal{B}$ a $\mathcal{B^\prime}$.
$\vec{a}_{(\mathcal{B^\prime})}=(-1,1,-1)$, $\vec{a}_{(\mathcal{B})}=(-2,1,3)$,

Jsou báze $\mathcal{B}$ a $\mathcal{B^\prime}$ ortonormální (uveďte důvod)?

$\mathcal{B^\prime}$ ano, $\mathcal{B}$ ne.

2.26

Vektor $\vec{a}$ má ve standardní kartézské bázi $\mathcal{E}$ složky $(1,1,2)$. Dále jsou zadány dvě báze $\mathcal{B}$ a $\mathcal{B^\prime}$, přičemž matice $\mathbf{R}$ přechodu z báze $\mathcal{E}$ do báze $\mathcal{B^\prime}$ má tvar

$$\mathbf{R}(\mathcal{E}\longmapsto\mathcal{B^\prime})= \left(\begin{array}{r} 1&1&0\\-1&1&0\\0&0&1 \end{array}\right).$$

Přechod mezi bázemi $\mathcal{B}$ a $\mathcal{B^\prime}$ je dán vztahy

$$\begin{array}{l c r c r c r} \vec{e}_1&=& & & -\vec{e}_2^{\,\,\prime}&-&2\,\vec{e}_3^{\,\,\prime},\\ \vec{e}_2&=&\dfrac{1}{2}\,\vec{e}_1^{\,\,\prime}&-&\dfrac{3}{2}\,\vec{e}_2^{\,\,\prime}&+& \vec{e}_3^{\,\,\prime},\\ \vec{e}_3&=& & & \vec{e}_2^{\,\,\prime}&+&3\,\vec{e}_3^{\,\,\prime}. \end{array} $$

Určete

matici $\mathbf{T}$ přechodu z báze $\mathcal{E}$ do báze $\mathcal{B}$,
$\mathbf{T}= \left(\begin{array}{r}1&-1&-2\\2&-1&1\\-1&1&3\end{array}\right)$
matici $\mathbf{S}$ přechodu z báze $\mathcal{B}$ do báze $\mathcal{E}$,
$\mathbf{S}= \left(\begin{array}{r}-4&1&-3\\-7&1&-5\\1&0&1\end{array}\right)$
složky vektoru $\vec{a}$ v bázích $\mathcal{B}$ a $\mathcal{B^\prime}$.
$\vec{a}_{(\mathcal{B})}=(-9,2,-6)$, $\vec{a}_{(\mathcal{B^\prime})}=(1,0,2)$

Jsou báze $\mathcal{B}$ a $\mathcal{B^\prime}$ ortonormální (uveďte důvod)?

$\mathcal{B^\prime}$ ne, $\mathcal{B}$ ne.

Je báze $\mathcal{B^\prime}$ ortogonální (prokažte)?

Ano.