9 Fourierovy řady
Metoda rozkladu obecných periodických funkcí na součet nekonečného počtu
sinových a kosinových vln byla pojmenována po francouzském matematiku Jean-Baptiste Josephu Fourierovi (1768–1830).
Fourierovy řady jsou v různé míře aplikovány ve většině fyzikálních oborů, např. v akustice, optice, kvantové fyzice, atd. Princip formulovaný nejprve pro Fourierovy řady byl později zobecněn v tzv. Fourierově analýze.
Libovolná periodická funkce $f(x)$ s periodou $T$, integrovatelná v intervalu $\langle x_0,x_0+T)$, může být vyjádřena jako následující nekonečná suma (Fourierova řada):
$$ f(x)=\dfrac{\text{a}_0}{2}+\sum_{k=1}^{\infty}\text{a}_k\cos(k\omega x)+\text{b}_k\sin(k\omega x), $$
9.1
kde $\omega=2\pi/T$. Fourierovy koeficienty $\text{a}_k,\,\text{b}_k$ lze stanovit následujícím způsobem:
$ \text{a}_0 =\dfrac{2}{T}\displaystyle\int_{x_0}^{x_0+T}f(x)\,\text{d} x, $
9.2
$ \text{a}_k =\dfrac{2}{T}\displaystyle\int_{x_0}^{x_0+T}f(x)\cos(k\omega x)\,\text{d} x, $
9.3
$ \text{b}_k =\dfrac{2}{T}\displaystyle\int_{x_0}^{x_0+T}f(x)\sin(k\omega x)\,\text{d} x. $
9.4
Fourierova transformace je zobecněním komplexních Fourierových řad. Nahradíme-li diskrétní Fourierovy koeficienty $a_k,b_k$
spojitou funkcí $F(\xi)\,\text{d}\xi$, potom za předpokladu $1/T\rightarrow \xi$ (frekvence) přejde (záměnou sumy za integrál) diskrétní Fourierova řada do spojité podoby
$$ {F}(\xi)=\int_{-\infty}^\infty f(x)\,\text{e}^{-2\pi\text{i}\xi x}\,\text{d} x,\qquad f(x)=\int_{-\infty}^\infty {F}(\xi)\,\text{e}^{2\pi\text{i}\xi x}\,\text{d}\xi. $$
9.5
Ve fyzice a v technických aplikacích se Fourierova transformace zapisuje častěji pomocí úhlové frekvence $\omega=2\pi\xi$.
Fourierova transformace $\mathcal{F}(f)=\widehat{f}$ (kde $\widehat{f}$ je tzv. Fourierův obraz funkce $f$, tj. vzoru) a
zpětná Fourierova transformace $\mathcal{F}^{-1}(\widehat{f})=f$ jsou potom (při jisté ztrátě symetrie) definovány jako:
$$ \widehat{f}(\omega)=\int_{-\infty}^\infty f(x)\,\text{e}^{-\text{i}\omega x}\,\text{d} x,\qquad f(x)=\frac{1}{2\pi}\int_{-\infty}^\infty \widehat{f}(\omega)\,\text{e}^{\text{i}\omega x}\,\text{d}\omega. $$
9.6
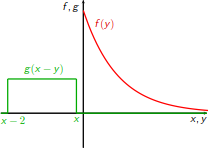
Zavedeme dále pojem konvoluce dvou funkcí $f(x),g(x)$ (viz obrázek 9.1 ), která je definována jako:
$$ (f\ast g)(x)=\int_{-\infty}^\infty f(y)\,g(x-y)\,\text{d} y, $$
9.7
kde ovšem $x$ a $y$ neznamenají dva různé souřadnicové směry, ale pouze dvě různé proměnné.
Fourierův obraz konvoluce funkcí $f(x),g(x)$ potom bude:
$$ \widehat{(f\ast g)}(\omega)=\int_{-\infty}^\infty(f\ast g)(x)\,\text{e}^{-\text{i}\,\omega x}\,\text{d} x=\int_{-\infty}^\infty \int_{-\infty}^\infty f(y)\,g(x-y)\,\text{e}^{-\text{i}\,\omega x}\,\text{d} x\,\text{d} y. $$
9.8
Pomocí transformace $\genfrac \{ \} {0pt}{0}{x-y=z}{y=y}$, jejíž Jakobián
$\det\left|\begin{array}{cc}\dfrac{\partial z}{\partial x}&\dfrac{\partial z}{\partial y}\\
\dfrac{\partial y}{\partial x}&\dfrac{\partial y}{\partial y}\end{array}\right|=
\det\left|\begin{array}{cr}1&-1\\0&1\end{array}\right|=1,$ dostáváme
$$ \int_{-\infty}^\infty\int_{-\infty}^\infty f(y)\,g(z)\,\text{e}^{-\text{i}\,\omega(y+z)}\,\text{d} y\,\text{d} z= \int_{-\infty}^\infty f(y)\,\text{e}^{-\text{i}\,\omega y}\,\text{d} y\int_{-\infty}^\infty g(z)\,\text{e}^{-\text{i}\,\omega z}\,\text{d} z=\widehat{f}(\omega)\,\widehat{g\,}(\omega). $$
9.9
Výsledný vztah můžeme tedy zapsat jednoduchým způsobem,
$$ \widehat{(f\ast g)}=\widehat{f}\,\widehat{g\,}, $$
9.10
Fourierův obraz konvoluce dvou funkcí $f(x),g(x)$ se rovná součinu jejich Fourierových obrazů.
Příklad konvoluce dvou funkcí ${f\ast g}$, které jsou původně zadány například ve tvaru
$ f(x)=\left\{ \begin{array}{r l} 0 &\,\,x\in(-\infty,0)\\ 3\,\text{e}^{-x} & \,\,x\in\langle 0,\infty), \end{array} \right.$
9.11
$ g(x)=\left\{ \begin{array}{r l}\label{konvice2} 0 &\,\,{x\in(-\infty,0)}\\ 1 &\,\,{x\in\langle 0,2\rangle}\\ 0 &\,\,x\in(2,\infty), \end{array}\right. $
9.12
znázorňuje obrázek 9.1 .
Obrázek 9.1: Schéma konvoluce ${f\ast g}$ funkcí $f(x)$, $g(x)$, původně popsaných rovnicemi 9.11 a 9.12
V obrázku 9.1a platí, že v rovnicích 9.13 , 9.14
je $x\in(-\infty,0)$, v obrázku 9.1b je $x\in\langle 0,2\rangle$,
v obrázku 9.1c je $x\in(2,\infty)$. Tvar výsledné funkce $({f\ast g})\,(x)$ je zakreslen modrou barvou, funkce je popsána v rovnici 9.18 , její hodnota se pro každé $x$ bude rovnat velikosti zvýrazněné plochy.
Funkce $f,g$ transformujeme podle rovnice 9.7 následujícím způsobem:
$ f(x)=3\,\text{e}^{-x} $
$\rightarrow\quad f(y)=3\,\text{e}^{-y}$
(9.13)
$ g(x)$
$\rightarrow\quad g\left(x-y\right) \quad=\quad g\left(z\right)$
(9.14)
kde potom pro funkci $g\left(z\right)$ (konvoluční jádro),
platí $g(z)=1$, pro $z\in\langle 0,2\rangle$, a tedy $y\in\langle x,x-2\rangle)$ a $g(z)=0$ pro $z\notin\langle 0,2\rangle$, a tedy $y\notin\langle x,x-2\rangle)$, zároveň také platí $\text{d} z=-\text{d} y$.
Protože $f(y)=0$ pro $y<0$, dostáváme tak tři oblasti integrace rovnice 9.7 :
$ x-2<0\wedge x<0 \quad$
(obrázek 9.1a )
(9.15)
$ x-2<0\wedge x\geq 0 \quad$
(obrázek 9.1b)
(9.16)
$ x-2\geq 0\wedge x> 0\quad$
(obrázek 9.1c)
(9.17)
Integrace rovnice 9.7 bude mít pro tyto tři oblasti podobu:
$$ ({f\ast g})\,(x)=\left\{ \begin{array}{l l} 0 &\text{pro }x\in(-\infty,0)\\[10pt] 3\displaystyle\int_0^x\,\text{e}^{-y}\,\text{d} y=3\left(1-\text{e}^{-x}\right) &\text{pro }x\in\langle 0,2\rangle,\\[10pt] 3\displaystyle\int_{x-2}^x\,\text{e}^{-y}\,\text{d} y=3\,\text{e}^{-x}\left(\text{e}^2–1\right) &\text{pro }x\in(2,\infty). \end{array}\right. $$
9.18
Výsledkem konvoluce dvou funkcí $f(x)$ a $g(x)$ bude tedy funkce $({f\ast g})\,(x)$, jejíž hodnota se pro každé $x\in(-\infty,\infty)$ bude rovnat velikosti zvýrazněné plochy na obrázku 9.1 .
9.1 Diskrétní Fourierovy řady
Příklady
Napište Fourierovu řadu pro následující periodické funkce s periodou $T$:
9.1
$f(x)=\dfrac{x^2}{\pi}$, $x\in\langle -\pi,\pi)$, $T=2\pi$
$\dfrac{\pi}{3}+\dfrac{4}{\pi}\sum\limits_{k=1}^\infty\dfrac{(-1)^k}{k^2}\cos(kx)$
9.2
$f(x)=\dfrac{x^2}{\pi}$, $x\in\langle 0,2\pi)$, $T=2\pi$
$\dfrac{4\pi}{3}+4\sum\limits_{k=1}^{\infty}\left[\dfrac{1}{k^2\pi}\cos(kx)-\dfrac{1}{k}\sin(kx)\right]$
9.3
$f(x)=|x|$, $x\in\langle -\pi,\pi)$, $T=2\pi$
$\dfrac{\pi}{2}+\dfrac{2}{\pi}\sum\limits_{k=1}^{\infty}\dfrac{(-1)^k-1}{k^2}\cos(kx)$
9.4
$f(x)=x|x|$, $x\in\langle −L,L)$, $T=2L$
$\dfrac{2L^2}{\pi^3}\sum\limits_{k=1}^{\infty}\dfrac{(2-\pi^2k^2)(-1)^k-2}{k^3}\sin\left(\dfrac{k\pi}{L}x\right)$
9.5
$f(x)=\dfrac{|x^3|}{x}$, $x\in\langle −1,1)$, $T=2$
$\dfrac{2}{\pi^3}\sum\limits_{k=1}^{\infty}\dfrac{(2-\pi^2k^2)(-1)^k-2}{k^3}\sin\left(k\pi x\right)$
9.6
$f(x)=\left\{
\begin{array}{r c l}
0 & &x\in\langle 0,1)\\
x-1 & &x\in\langle 1,2)
\end{array} \right.$, $T=2$
$\dfrac{1}{4}+\sum\limits_{k=1}^{\infty}\left[\dfrac{1-(-1)^k}{k^2\pi^2}\cos(k\pi x)-\dfrac{1}{k\pi}\sin(k\pi x)\right]$
9.7
$f(x)=\text{e}^{\text{a} x}$, $x\in\langle -\pi,\pi)$, konstanta $\text{a}\ne 0$, $T=2\pi$
$\dfrac{2}{\pi}\sinh(\text{a}\pi)\left[\dfrac{1}{2\text{a}}+\sum\limits_{k=1}^{\infty}
\dfrac{(-1)^k}{\text{a}^2+k^2} \left(\text{a}\cos(kx)-k\sin(kx)\right)\right]$
9.8
$f(x)=(x-1)(x-3)$, $x\in\langle 1,3)$, $T=2$
$-\dfrac{2}{3}+\dfrac{4}{\pi^2}\sum\limits_{k=1}^{\infty}\dfrac{(-1)^k}{k^2}\cos(k\pi x)$
9.9
$f(x)=\dfrac{x}{2L}$, $x\in\langle 0,2L)$, $T=2L$
$\dfrac{1}{2}-\dfrac{1}{\pi}\sum\limits_{k=1}^{\infty}\dfrac{1}{k}\sin\left(\dfrac{k\pi}{L}x\right)$
9.10
$f(x)=x^4$, $x\in\langle -1,1)$, $T=2$
$\dfrac{1}{5}+\dfrac{8}{\pi^4}\sum\limits_{k=1}^{\infty}(-1)^k\dfrac{k^2\pi^2–6}{k^4}\cos\left(k\pi x\right)$
9.11
$f(x)=\text{sgn}\left[\sin\left(\dfrac{\pi x}{L}\right)\right]$, $x\in\langle 0,2L)$, $T=2L$
$\dfrac{4}{\pi}\sum\limits_{k=1}^{\infty}\dfrac{1}{2k+1}\sin\left[\dfrac{(2k+1)\pi}{L}x\right]$
9.12
$f(x)=\left\{
\begin{array}{r c l}
-x & &x\in\langle -1,0)\\
x & &x\in\langle 0,1)
\end{array} \right.$, $T=2$
$\dfrac{1}{2}-\dfrac{4}{\pi^2}\sum\limits_{k=0}^{\infty}\dfrac{\cos\left[(2k+1)\pi x\right]}{(2k+1)^2}$
9.13
$f(x)=\left\{
\begin{array}{r c l}
1 & &x\in\left\langle 0,\,\dfrac{\pi}{2}\right)\\[6pt]
-1 & &x\in\left\langle -\dfrac{\pi}{2},\,0\right),\\[6pt]
0 & &|x|\in\left\langle \dfrac{\pi}{2},\,\pi\right)
\end{array}\right. T=2\pi$
$\dfrac{2}{\pi}\sum\limits_{k=1}^{\infty}\dfrac{1}{k}\left[1-\cos\left(\dfrac{k\pi}{2}\right)\right]\sin(kx)$
9.14
$f(x)=\left\{
\begin{array}{r c l}
0 & & x\in\left\langle -1,-\dfrac{1}{2}\right)\\
\cos 3\,\pi x & & x\in\left\langle -\dfrac{1}{2},\,\dfrac{1}{2}\right),\\
0 & & x\in\left\langle\dfrac{1}{2},\,1\right)
\end{array}\right. T=2$
$−\dfrac{1}{3\pi}+\dfrac{6\cos(2\pi x)}{5\pi}+\dfrac{\cos(3\pi x)}{2}+
\dfrac{6}{\pi}\sum\limits_{k=4}^{\infty}\dfrac{1}{k^2−9}\cos\left(\dfrac{k\pi}{2}\right)\cos(k\pi x)$
9.15
$f(x)=\left\{
\begin{array}{c c l}
1 & &x\in\left\langle -1,0\right)\\[4pt]\dfrac{1}{2} & & x=0\\[6pt]
x & &x\in\left(0,1\right)\end{array}\right.$, $T=2$
$
\dfrac{3}{4}+\sum\limits_{k=1}^{\infty}\dfrac{(-1)^k-1}{k^2\pi^2}\cos(k\pi x)-\dfrac{1}{k\pi}\sin(k\pi x)$
9.16
$f(x)=\left\{
\begin{array}{r c l}
\dfrac{4}{\pi}x & & x\in\left\langle 0,\,\dfrac{\pi}{2}\right)\\[7pt]
-\dfrac{4}{\pi}x & & x\in\left\langle-\dfrac{\pi}{2},\,0\right)\end{array}\right.$, $T=\pi$
$
1-\dfrac{8}{\pi^2}\sum\limits_{k=1}^\infty\dfrac{\cos\left[2\left(2k-1\right)x\right]}{(2k-1)^2}$
9.17
$f(x)=\left\{
\begin{array}{c c l}
x\left(1-x\right)& & x\in\left\langle 0,1\right)\\
0& & x\in\left\langle-1,0\right)\end{array}\right.$
$
\dfrac{1}{12}-\dfrac{1}{\pi^2}\sum\limits_{k=1}^\infty\left[\dfrac{1}{k^2}\left(1+\cos k\pi\right)\cos(k\pi x)-\dfrac{2}{k^3\pi}\left(1-\cos k\pi\right)\sin(k\pi x)\right]$
9.18
$f(x)=\left|\sin x\right|$, $x\in\langle -\pi,\pi)$, $T=2\pi$
$\dfrac{2}{\pi}-\dfrac{4}{\pi}\sum\limits_{k=1}^{\infty}\dfrac{1}{\left(4k^2−1\right)}\cos(2kx)$
9.19
$f(x)=\left|\cos x\right|$, $x\in\langle -\pi,\pi)$, $T=2\pi$
$\dfrac{2}{\pi}-\dfrac{4}{\pi}\sum\limits_{k=1}^{\infty}\dfrac{(-1)^k}{\left(4k^2−1\right)}\cos(2kx)$
9.20
$f(x)=\sin x\cos x,$ $x\in\left\langle −1,1\right)$
$\pi\sin(2)\sum\limits_{k=1}^\infty\dfrac{k(-1)^k}{4-k^2\pi^2}\sin(k\pi x)$
9.21
$f(x)=|x|+\text{a},$ $x\in\langle −L,L)$, kde $\text{a}$ je konstanta.
$\text{a}+\dfrac{L}{2}+\dfrac{2L}{\pi^2}\sum\limits_{k=1}^\infty\dfrac{(-1)^k-1}{k^2}\,\cos\left(\dfrac{k\pi}{L}x\right)$
9.22
$f(x)=\left\{\begin{array}{l c l} x-\text{a} & & x\in\langle -L,0)\\[2pt]
x+\text{a} & & x\in\langle 0,L)
\end{array}\right.$, kde $\text{a}$ je konstanta.
$\dfrac{2}{\pi}\sum\limits_{k=1}^\infty\dfrac{\text{a}-(\text{a}+L)(-1)^k}{k}\sin\left(\dfrac{k\pi}{L}x\right)$