[Další] [Předchozí] [Předchozí – na konec] [Na konec] [Výše]

Kapitola 1
Pojem funkce více proměnných

Reálná funkce jedné reálné proměnné, stručně funkce jedné proměnné, je zobrazení z ℝ do ℝ. Zobecněním tohoto pojmu je zobrazení z ℝn (n ≥ 2) do ℝ, které se nazývá funkce více proměnných.

Cílem této kapitoly je naučit se určovat pro funkci dvou a více proměnných její definiční obor a graf. Přestože tato kapitola jako jediná neobsahuje žádnou matematickou větu, je svým zaměřením na geometrii v ℝ2 a ℝ3 fundamentální.

Definice 1.1. Nechť M ⊆ ℝn, n ≥ 1,M≠∅. Zobrazení f : M → ℝ se nazývá reálná funkce n reálných proměnných a množina M se nazývá definiční obor této funkce a značí se 𝒟(f).

 

Z předchozí definice vyplývá, že po formální stránce funkce f : M → ℝ je množina uspořádaných dvojic [x,y] ∈ M × ℝ, x = [x1,…,xn] (tj. relace na M × ℝ), která má následující vlastnosti:

1. x ∈ M, y ∈ ℝ.

2. Ke každému bodu x = [x1,…,xn] ∈ M existuje právě jedno číslo y (bod prostoru ℝ) tak, že [x,y] ∈ f.

Obraz bodu x = [x1,…,xn] ∈ M v zobrazení f, tj. reálné číslo y takové, že [x,y] ∈ f, označujeme f(x) nebo f(x1,…,xn) a nazývá se hodnota funkce f nebo také funkční hodnota v bodě x = [x1,…,xn].

Z definice funkce více proměnných vyplývá, že tato funkce je jednoznačně určena udáním jejího definičního oboru 𝒟(f) a předpisem, kterým je každému bodu x = [x1,…,xn] ∈𝒟(f) přiřazena funkční hodnota f(x). Pokud je předpis dán vzorcem a není udán definiční obor funkce, pak definičním oborem rozumíme množinu všech bodů x ∈ ℝn, pro něž má tento vzorec smysl.

Pro n = 2 budeme místo f(x1,x2) psát f(x,y) a pro n = 3 místo f(x1,x2,x3) píšeme f(x,y,z).

Příklad 1.1. i) Zobrazte v rovině definiční obor funkce

∘(-----------------)--------------- f(x,y) = x2 + (y −-2)2-− 1 (x2 + y2 − 6x). 4
Řešení. Výraz pod odmocninou musí být nezáporný, tj. musí být splněna podmínka
( 2 )( ) (y −-2)-+ x2 − 1 x2 + y2 − 6x ≥ 0. 4
To nastane, právě když
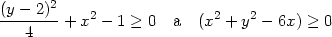
(y −-2)2 2 2 2 4 + x − 1 ≥ 0 a (x + y − 6x) ≥ 0
nebo
(y − 2)2 --------+ x2 − 1 ≤ 0 a (x2 + y2 − 6x) ≤ 0. 4
PICT

Rovnice (y−2)2 --4-- + x2 = 1 je rovnicí elipsy se středem v bodě [0,2] a poloosami délek a = 1 a b = 2, rovnice x2 + y2 − 6x = 0 je rovnicí kružnice se středem v bodě [3,0] a poloměrem r = 3, neboť tuto rovnici lze převést na tvar (x − 3)2 + y2 = 9. Množina všech bodů [x,y] ∈ ℝ2 splňující výše uvedené nerovnosti, tj. definiční obor funkce f, je znázorněna na vedlejším obrázku. Je to uzavřená množina v ℝ2.

ii) Zobrazte v rovině definiční obor funkce

∘ ---------√--- f(x,y)= arccos(x2 +y2− 1)+ ∣x∣+ ∣y∣− 2.

 

Řešení. Definičním oborem funkce arccos je interval [−1,1], první sčítanec je tedy definován pro [x,y] splňující nerovnosti

− 1 ≤ x2 + y2 − 1 ≤ 1,
PICT

tj.

0 ≤ x2 + y2 ≤ 2,
což je vnitřek a hranice kruhu se středem v počátku a poloměrem r = √ -- 2. Definičním oborem druhého sčítance je množina bodů [x,y] splňující nerovnost ∣x∣ + ∣y∣−√ -- 2 ≥ 0. Načrtněme v rovině křivku danou rovnicí ∣x∣ + ∣y∣ = √ -- 2. V prvním kvadrantu je tato rovnice ekvivalentní rovnici x + y = √-- 2, což je rovnice přímky. Ve zbývajících kvadrantech postupujeme obdobně a obdržíme kosočtverec načrtnutý na vedlejším obrázku. Definičním oborem funkce f je množina vyšrafovaná na tomto obrázku. Tato množina je uzavřená v ℝ2.

iii) Zobrazte v rovině definiční obor funkce f(x,y) = ln(y ln(y − x)).

Řešení. Logaritmovaný výraz musí být kladný, musí být tedy splněna nerovnost y ln(y − x) > 0, která je ekvivalentní dvojici nerovností

ln(y − x) > 0, y > 0; ln(y − x) < 0, y < 0,
jež jsou dále ekvivalentní systémům nerovností
y > 0, y − x > 1 a y < 0, y − x < 1, y − x > 0
(poslední nerovnost plyne z definičního oboru funkce ln(y − x)). Řešením těchto dvou systémů nerovností je množina načrtnutá na obr. 1.1 . Je to otevřená množina v ℝ2.

iv) Zobrazte definiční obor funkce f(x,y) = arcsinx- y2 + arcsin(1 − y).

Řešení. Definičním oborem funkce arcsin je interval [−1,1]. Proto musí být splněny podmínky:

x − 1 ≤ -2-≤ 1, tj. y2 ≥ − x, y2 ≥ x, y ⁄= 0 y

a zároveň −1 ≤ 1 − y ≤ 1, tj. y ∈ [0,2]. Celkem tedy

𝒟(f ) = {[x,y] : y2 ≥ − x, y2 ≥ x, y ∈ (0,2]},
tato množina je načrtnuta na obr. 1.2. Je to množina, která není ani otevřená, ani uzavřená v ℝ2 (neboť [0,0]∉𝒟(f)).

 

 

PICT
obr. 1.1 z = ln(y ln(y −x))
PICT
obr. 1.2 z = arcsin x2- y + arcsin(1 −y)

Definice 1.2. Nechť f je funkce n proměnných definovaná na množině M ⊆ ℝn, n ≥ 2. Grafem funkce f nazýváme množinu bodů

G(f ) = {[x,y] ∈ ℝn+1 : x = [x ,...,x ] ∈ M, y = f (x)}. 1 n

 

 

PICT

obr. 1.3: Souřadné stěny ρxy,ρxz,ρyz

Pro funkci dvou proměnných, tj. n = 2, je grafem funkce množina bodů v trojrozměrném prostoru. V příkladech, se kterými se zde setkáme, to bude vždy nějaká trojrozměrná plocha. K získání názorné představy, jaký je tvar a průběh této plochy, nám pomohou řezy rovinami z = 0, y = 0, x = 0 (což jsou rovnice souřadných stěn ρxy,ρxz,ρyz, viz obr. 1.3 ) a rovinami s nimi rovnoběžnými.

Definice 1.3. Nechť M ⊆ ℝ2 a f : M → ℝ je funkce dvou proměnných definovaná na M, c ∈ ℝ. Množinu

fc = {[x, y] ∈ M : f(x,y) = c}
nazýváme vrstevnice funkce f na úrovni c.

 

Pojem vrstevnice funkce lze samozřejmě analogicky definovat i pro funkce n proměnných, n ≥ 3, zde však ztrácíme názorný „geografický“ význam. Chápeme-li graf funkce dvou proměnných jako reliéf krajiny, pak vrstevnice funkce na úrovni c je množina všech bodů s nadmořskou výškou rovnou c, tj. náš pojem vrstevnice je totožný s geografickým významem tohoto slova.

Příklad 1.2. i) Pomocí vrstevnic a řezů rovinami ρxz,ρyz zobrazte graf funkce f(x,y) = ∘ ------- x2 + y2.

Řešení. Vrstevnice funkce na úrovni k > 0 jsou dány rovnicemi

k = ∘x2-+-y2, tj. k2 = x2 + y2,
což jsou kružnice se středem na ose z a poloměrem k, viz obr. 1.4.

Řez rovinou ρyz, tj. x = 0, dává z = --- ∘ y2 = ∣y∣. Řezem je lomená čára s vrcholem v počátku daná rovnicí z = ∣y∣. Podobně řez rovinou y = 0 dává z = ∣x∣. V obou případech je řezem lomená čára s vrcholem v počátku o rovnici z = ∣y∣, resp. z = ∣x∣, viz obr. 1.5 , 1.6 . (V terminologii technického kreslení a zobrazovacích metod se vlastně jedná o průmět do svislých souřadných nárysen, tj. nárys a bokorys.)

PICT
obr. 1.4 Půdorys
PICT
obr. 1.5 Bokorys
PICT
obr. 1.6 Nárys

Na základě získaných výsledků již můžeme říci, že grafem funkce z = ∘ -2----2 x + y je rotační kužel s vrcholem v počátku a hlavní osou z, nacházející se v poloprostoru z ≥ 0, viz obr. 1.10. Na tomto obrázku je znázorněn i dolní kužel, který je grafem funkce z = −∘ ------- x2 + y2.

ii) Zobrazte v ℝ3 graf funkce f(x,y) = x2 a2 + y2- b2, a,b > 0.

Řešení. Podobně jako v předchozím příkladu jsou vrstevnice dány rovnicemi

x2 y2 x2 y2 k = a2-+ b2, tj. ka2-+ kb2 = 1,
což jsou rovnice elipsy se středem v počátku a poloosami a√ -- k, b√ -- k, viz obr. 1.7 . Řezy rovinami y = 0, x = 0 dávají
2 2 z = x-, z = y-, a2 b2
což jsou rovnice parabol s vrcholem v počátku souřadných stěn ρxz a ρyz, viz obr. 1.8 , 1.9 . Celkem vidíme, že grafem je plocha, která se nazývá eliptický paraboloid. Tato plocha je prostorově v okolí počátku znázorněna na obr. 1.11 .
PICT
obr. 1.7 Půdorys
PICT
obr. 1.8 Bokorys
PICT
obr. 1.9 Nárys

iii) Zobrazte v ℝ3 definiční obor funkce f(x,y,z) = ln(−z2 −x2 −y2 + 1).

Řešení. Logaritmická funkce je definována jen pro kladná čísla. Proto musí být −z2 − x2 − y2 + 1 > 0, tj. x2 + y2 + z2 < 1, a tedy

𝒟(f) = {[x,y,z] ∈ ℝ3 : x2 + y2 + z2 < 1}.
V řezech rovinami z = 0,y = 0,x = 0 postupně dostáváme x2 + y2 < 1, x2 + z2 < 1, y2 + z2 < 1, což jsou body uvnitř kružnice se středem v počátku a poloměru r = 1, celkem je tedy definičním oborem vnitřek koule se středem v bodě [0,0,0] a poloměrem r = 1, je to otevřená množina v ℝ3.

 

 

PICT
obr. 1.10 z = ±∘------ x2 +y2
PICT
obr. 1.11 z = xa22 + yb22

Příklad 1.3. i) Načrtněte v rovině vrstevnice funkce z = e-2x-- x2+y2 .

Řešení. Vrstevnice funkce mají rovnici c = e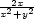-22x-2 x +y a odtud lnc = -2x-- x2+y2. Označíme-li nyní lnc = k, postupnými úpravami dostáváme

k = --2x--- ⇐ ⇒ k(x2 + y2) = 2x ⇐ ⇒ x2 − 2-x+ y2 = 0, x2 + y2 k
a tedy pro k≠0 (tj. c≠1),
(x − 1-)2 + y2 = 1-. k k2
PICT

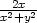Z poslední rovnice je již vidět, že vrstevnicemi dané funkce pro c≠1 jsou kružnice se středem S = [1 k,0] = [-1- lnc,0] a poloměrem r = -1 ∣k∣ = --1- ∣lnc∣ procházející počátkem, avšak bez počátku (neboť pro bod [0,0] není funkce definována). Pro c = 1 dostáváme 0 = 2x x2+y2, tj. x = 0, vrstevnicí dané funkce pro c = 1 je tedy osa y (bez počátku).

ii) Načrtněte vrstevnice funkce z = ∣x∣−∣y∣ + ∣x − y∣.

Řešení. Nejprve se zbavíme ve vyjádření funkční závislosti absolutních hodnot. Provedeme diskusi v jednotlivých kvadrantech.

Ia) x ≥ 0,y ≥ 0,x ≥ y ⇒ z  = x − y + x − y = 2(x − y).

Ib)  x ≥ 0,y ≥ 0,x < y ⇒ z = x − y − x + y = 0.

II) x < 0, y ≥ 0, (zde vždy x ≤ y)   ⇒ z  = −x − y − x + y = −2x.

Obdobným způsobem získáme vyjádření funkční závislosti bez absolutních hodnot ve zbývajících dvou kvadrantech a jako výsledek obdržíme situaci znázorněnou na obr. 1.12. Protože pro libovolná [x,y] ∈ ℝ2 platí nerovnost ∣x − y∣≥∣y∣−∣x∣ (zdůvodněte proč), je vždy f(x,y) ≥ 0, tj. pro c < 0 je fc = 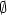∅. Pro c ≥ 0 načrtneme v jednotlivých sektorech křivku ∣x∣−∣y∣ + ∣x − y∣ = c a pro c = 0,1,2,3 je výsledek znázorněn na obr. 1.13 .

 

PICT
obr. 1.12 z = ∣x −y∣ + ∣x∣−∣y∣
PICT
obr. 1.13 Vrstevnice

Cvičení PIC

1.1.  Zobrazte v rovině definiční obory funkcí:

 

a) z = ∘ ------------ 1− x2 − 4y2 g) z = ∘ x2+y2−x-- 2x−x2−y2

 

b) z = ∘ ------------- (x2- y2) 1− 9 + 4 h) z = arccos-x-- x+y

 

c) z = ln(x + y) i) z = ∘ ------------ 1 − (x2 + y)2

 

d) z = ∘(x2--+-y2 −-1)(4-−-x2 −-y2) j) z = √ ----- ----4x−-y2-- ln(1− x2−y2)

 

e) z = arcsinx y −--1-- ∣y∣− ∣x∣ k) z = ln[xln(y − x)]

 

f) z = √------ 1 − x2 + ∘ ------ 1− y2 l) z = ∘ -------------2----------- (1 − x2 − y2)(x4 + y2 − 2y)

 

 

1.2.  Načrtněte vrstevnice funkcí:

a) z = x2 + y2 c) z = xy, kde x > 0

 

b) z = x2 − y2 d) z = √ ---- x ⋅y

 

 

1.3.  Pomocí vrstevnic a řezů rovinami ρxz,ρyz načrtněte v prostoru grafy funkcí:

a) z = 2 − x − y c) z = ∘ -----2----2 1 − x − y d) z = 1 2(x2 − y2)

 

e) z = 2x2+13y2- b) z = x2 + y2 f) z = 2 −∘ ------- x2 + y2

 

 

1.4.  Určete definiční obory funkcí:

a) u = ∘1-+-x2-−-y2-−-z2 f) u = ln(xyz)

 

b) u = √----- 1 − x + √----- y + 3 + √-- z g) u = ∘ -----2---2----2- 1− xa2 − yb2-− zc2

 

c) u = ∘ -----2----2---2 1 + x + y − z h) u = ∘ ----x2---y2---z2- 1− a2 − b2 − c2

 

d) u = arccos√--z2--2 x +y i) u = arcsinxy + arcsiny + arccosz3

 

e) u = ∘ ---------------- x2- y2 z2 1+ a2 + b2 − c2 j) u = ln(−x2 − y2 + 2z)

 

 

 

 

∗

Většina učitelů ztrácí čas tím, že klade otázky, jejichž cílem je zjistit, co žák neumí, zatímco pravé umění tázat se spočívá v tom, že má odhalit, co žák umí nebo je schopen umět. (A. Einstein)

∗

[Další] [Předchozí] [Předchozí – na konec] [Na začátek] [Výše]