Přírodovědecká fakulta Masarykovy univerzity
RNDr. Marie Forbelská, Ph.D., Mgr. Jan Koláček, Ph.D.
Úvod do matematické statistiky
1. Náhodný výběr a výběrové charakteristiky
V teorii pravděpodobnosti se předpokládá, že
- je známý pravděpodobnostní prostor $(\Omega,\mathcal{A},P)$
- a že také známe rozdělení pravděpodobnosti náhodných veličin (resp. náhodných vektorů), které na tomto pravděpodobnostním prostoru uvažujeme.
V matematické statistice však
- máme k dispozici výsledky $n$ nezávislých pozorování hodnot sledované náhodné veličiny $X$, které se ve statistice říká statistický znak, tj. máme $$x_1=X(\omega_1),\ldots,x_n=X(\omega_n),\; \omega_1,\ldots,\omega_n\in \Omega$$
- a na základě těchto pozorování chceme učinit výpověď o rozdělení zkoumané náhodné veličiny.
Definujme nejprve základní pojmy matematické statistiky. Základním pojmem matematické statistiky je pojem náhodného výběru.
Náhodný vektor $\mathbf{X}_n=(X_1,\ldots,X_n)'$ nazýváme náhodným výběrem z rozdělení pravděpodobnosti $P$, pokud
| $(i)$ | $X_1, \ldots, X_n$ jsou nezávislé náhodné veličiny, |
| $(ii)$ | $X_1, \ldots, X_n$ mají stejné rozdělení pravděpodobnosti |
Číslo $n$ nazýváme rozsah náhodného výběru. Libovolný bod $ \mathbf{x}_n=(x_1,\ldots,x_n)'$, kde $x_i$ je realizace náhodné veličiny $X_i$ ($i=1,\ldots,n$), budeme nazývat realizací náhodného výběru $\mathbf{X}_n=(X_1,\ldots,X_n)'$. Množinu všech hodnot, kterých může náhodný výběr nabýt, nazýváme výběrový prostor a budeme jej značit $\mathcal{X}$.
Základní dělení matematické statistiky je dané strukturou množiny všech možných rozdělení (označme ji $\mathcal{P}$) náhodného výběru $\mathbf{X}$. Velmi často vybíráme do množiny $\mathcal{P}$ jen rozdělení, která jsou stejného typu a která závisí pouze na nějakém (skalárním či vícerozměrném) parametru. Tento parametr se většinou značí $\boldsymbol\theta$ a pravděpodobnostní míry z množiny $\mathcal{P}$ symbolem $P_{\boldsymbol\theta}$. Přitom předpokládáme, že parametr $\boldsymbol\theta$ nabývá hodnot z nějaké množiny $\boldsymbol\Theta$.
Nechť náhodný výběr $\mathbf{X}_n=(X_1,\ldots,X_n)'$ je z rozdělení, které je dáno distribuční funkcí $F(x,\boldsymbol\theta),\;\boldsymbol\theta\in\boldsymbol\Theta$. Zkráceně budeme značit:
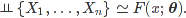
Nyní se zmiňme o tzv. rodinách rozdělení.
Cílem teorie odhadu je na základě náhodného výběru odhadnout
- rozdělení pravděpodobnosti,
- popřípadě některé parametry tohoto rozdělení,
- anebo nalézt odhad nějaké funkce parametrů $\boldsymbol \theta$, tj. $\gamma(\boldsymbol\theta)$.
Funkci $\gamma(\boldsymbol\theta)$ nazýváme parametrickou funkcí. V matematické statistice se pro funkce, pomocí kterých budeme odhady provádět, nazývají statistikou. (Tyto funkce jsou navíc měřitelné).
Ukážeme, jakým způsobem lze například informaci obsaženou
v náhodném výběru zužitkovat k popisu distribuční funkce.
Mějme 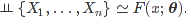
Potom $I_1(x),\ldots,I_n(x)$ jsou nezávislé náhodné veličiny
se stejným alternativním rozdělením pravděpodobností s parametrem $\pi\in(0,1)$, tj.
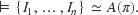 Parametr $\pi$ je roven pravděpodobnosti úspěchu, tj.
Parametr $\pi$ je roven pravděpodobnosti úspěchu, tj.
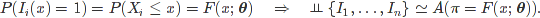
Položme
$$\begin{array}{lcl} Y(x) & = & \sum_{i=1}^n I_i(x) \\[1ex] F_n(x) & = & \frac{Y(x)}{n} \end{array}$$a postupně počítejme
$${EF_n(x)}=E\tfrac{Y(x)}{n}=\tfrac{1}{n} Y_n =\tfrac{1}{n}\sum_{i=1}^n I_i(x)=\tfrac{1}{n}\cdot n\;F(x;\boldsymbol\theta) ={F(x;\boldsymbol\theta)}.$$Protože posloupnost $\{F_n(x)\}_{n=1}^\infty$ splňuje jak slabý, tak silný zákon velkých čísel, tak platí
$$\begin{array}{lcl} \lim_{n\to \infty}P(|F_n(x)-F(x;\boldsymbol\theta)|\geq \varepsilon) & = & 0 \\[1ex] P(\lim_{n\to \infty}F_n(x)=F(x;\boldsymbol\theta)) & = & 1 \end{array}$$
Z uvedených vztahů je vidět, že pokud rozsah výběru bude dostatečně velký, lze distribuční funkci rozdělení, z něhož výběr pochází, dostatečně přesně aproximovat pomocí výběrové (empirické) distribuční funkce.
Předpokládejme, že rozdělení, z něhož výběr pochází, má konečné druhé momenty se střední hodnotou $\mu$ a rozptylem $\sigma^2$, což budeme dále značit
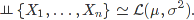
Tedy pro každé $i=1,\ldots,n$ platí
$$\begin{array}{lcl} EX_i & = & \mu \\ DX_i & = & \sigma^2 \end{array}.$$Potom tyto charakteristiky zřejmě závisí na parametru $\boldsymbol\theta$, neboť
$$\begin{array}{lcl} \mu & = & \int_{-\infty}^\infty xdF(x;\boldsymbol\theta) \\[1ex] \sigma^2 & = &\int_{-\infty}^\infty (x-\mu)^2dF(x;\boldsymbol\theta) \end{array},$$proto bude lépe značit je $\mu(\boldsymbol\theta)$ a $\sigma^2(\boldsymbol\theta$ místo $\mu$ a $\sigma^2$.
Všimněme si dále, že pro každé $x\in \mathbb{R}$ je $F_n(x)=F_n(X_1,\ldots,X_n)$ statistikou, tím také náhodnou veličinou (která nabývá hodnot mezi nulou a jedničkou) a tím i funkcí elementárního jevu $\omega\in\Omega$.
Zvolíme-li $\omega$ libovolně, ale pevně a uvažujeme-li {$F_n(x)$} jako funkci proměnné $x$, pak lze snadno odvodit, že je tato funkce distribuční funkcí nějaké náhodné veličiny a lze zavést její střední hodnotu a rozptyl
$$\begin{array}{lcl} \mu_n & = & \int_{-\infty}^\infty xdF_n(x;\boldsymbol\theta)= \tfrac{1}{n}\sum_{i=1}^n X_i \\[1ex] \sigma_n^2 & = &\int_{-\infty}^\infty (x-\mu)^2dF(x;\boldsymbol\theta) =\tfrac{1}{n}\sum_{i=1}^n (X_i-\mu_n)^2 \end{array}$$Zřejmě $\mu_n$ a $\sigma_n^2$ jsou borelovské funkce náhodného výběru a tedy statistiky a lze je považovat za odhady parametrických funkcí $\mu(\boldsymbol\theta)$ a $\sigma^2(\boldsymbol\theta)$. Lze očekávat, že čím bude rozsah náhodného výběru větší, tím bude odhad uvedených parametrických funkcí kvalitnější.
Odhadem parametrické funkce $\gamma(\boldsymbol\theta)$ budeme rozumět nějakou statistiku $^{\scriptscriptstyle{\mathrm{T}}}n$, která bude pro různé náhodné výběry kolísat kolem $\gamma(\boldsymbol\theta)$.
Statistika $^{\scriptscriptstyle{\mathrm{T}}}n$ závisí na parametru $\boldsymbol\theta$ prostřednictvím distribuční funkce rozdělení, z něhož výběr pochází.
Také rozdělení této statistiky, tj. náhodné veličiny, závisí na parametru $\boldsymbol\theta$.
Proto střední hodnotu a rozptyl této statistiky budeme značit $E_{\boldsymbol\theta} T_n$ a $D_{\boldsymbol\theta} T_n$.
Nechť $\mathbf{X}_n=(X_1,\ldots,X_n)'$ je náhodný výběr rozsahu $n$ z rozdělení s distribuční funkcí $F(x;\boldsymbol\theta)$, $\boldsymbol\theta\in\boldsymbol\Theta$. Potom statistika
| $\bar{X}_n=\bar{X}=\tfrac{1}{n}\sum_{i=1}^n X_i$ | se nazývá | výběrový průměr |
| $S^2=\tfrac{1}{n-1}\sum_{i=1}^n (X_i-\bar{X})^2$ | výběrový rozptyl | |
| $S=\sqrt{S^2}$ | výběrová směrodatná odchylka | |
| $F_n(x)=\tfrac{1}{n}\sum\limits_{i=1}^n I_{(-\infty,x\gt }(X_i)$ | výběrová (empirická) distribuční funkce |
ÚMS, Přírodovědecká fakulta, Masarykova univerzita |
Návrat na úvodní stránku webu, přístupnost |
| Servisní středisko pro e-learning na MU
| Fakulta informatiky Masarykovy univerzity, 2013
Centrum interaktivních a multimediálních studijních opor pro inovaci výuky a efektivní učení | CZ.1.07/2.2.00/28.0041

