A Křivočaré souřadnice

Většina jevů v přírodě (a tedy i fyzikálních dějů) neprobíhá přísně pravoúhle a není vhodné a často ani schůdné je jednoduše popisovat pomocí kartézské metriky. V tom případě je výhodné zvolit takovou souřadnou soustavu (zpravidla křivočarou), která co nejlépe odpovídá geometrii popisovaného děje. Nejčastěji používanými křivočarými souřadnými soustavami jsou soustava válcová (cylindrická) a soustava kulová (sférická). Dále existuje řada speciálních křivočarých souřadných soustav, např. eliptická, parabolická, kónická, atd., včetně soustav neortogonálních, tj. takových, kdy jednotlivé souřadnicové směry nesvírají pravý úhel. Zvládnutí matematického aparátu, popisujícího křivočaré souřadnice, jejich vztahy a vzájemné převody, je pro fyzikální praxi nezbytné. V následujících poznámkách si ukážeme základní principy a praktické postupy při počítání v kartézských, válcových a kulových souřadných soustavách.

A.1 Kartézská soustava

Ačkoli kartézská soustava vlastně nepatří mezi křivočaré soustavy, uvádíme ji zde jako základní a nejjednodušší ortogonální souřadnou soustavou, na níž si názorně ukážeme základní vztahy a geometrické principy, které v rámci složitějších, skutečně křivočarých souřadných soustav již pouze analogicky upřesníme a aplikujeme. Její zásadní předností je, že (jednotkové) vektory kartézské báze,

$$ \vec{e}_x=\mathbf{\hat{x}}=(1,0,0),\quad\vec{e}_y=\mathbf{\hat{y}}=(0,1,0),\quad\vec{e}_z=\mathbf{\hat{z}}=(0,0,1), $$

A.1

jsou konstantní (mají stále stejnou velikost a stále stejný směr), derivace těchto vektorů jsou tedy nulové.V dalším textu budeme jednotkové vektory zapisovat ve stříškovém tvaru, tedy např. $\mathbf{\hat{x}}\quad$ místo $\vec{e}_x$. Pro druhou mocninu vzdálenosti dvou bodů v diferenciálním tvaru platí

$ \text{d} s^2=\text{d} x^2+\text{d} y^2+\text{d} z^2$, což lze zobecnit tzv. metrickou formou, $\text{d} s^2=g_{ij}\,\text{d} x^i\,\text{d} x^j$,

A.2

kde indexy $i,j$ značí jednotlivé souřadnicové směry ($i,j=x,y,z$) a zároveň tak určují jednotlivé složky $3\times 3$ metrického tenzoru. Kovariantní metrický tenzor $g_{ij}$ kartézské soustavy má tedy elementární tvar jednotkové matice. Význam kontravariantního metrického tenzoru $g_{ij}$ kartézské soustavy je formálně určen druhou mocninou velikosti vektoru

$$ \left(\frac{\partial}{\partial s}\right)^2=g^{ij}\frac{\partial}{\partial x_i}\frac{\partial}{\partial x_j}= \left(\frac{\partial}{\partial x}\right)^2+\left(\frac{\partial}{\partial y}\right)^2+\left(\frac{\partial}{\partial z}\right)^2. $$

A.3

Zároveň musí pro každou metriku obecně platit $g_{ij}\,g^{ij}=\mathbf{1}$, kovariantní a kontravariantní metrický tenzor tak budou vždy tvořit vzájemně inverzní matice. V kartézské soustavě budou mít tedy tvar

$$ g_{ij}= \begin{pmatrix} 1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1 \end{pmatrix},\quad g^{ij}= \begin{pmatrix} 1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1 \end{pmatrix}. $$

A.4

nahoru

A.1.1 Diferenciální operátory

Gradient skalární funkce $f=f\,(x,\,y,\,z)$ je v kartézské soustavě definován jako vektor ve tvaru

$$\vec{\nabla}f=\text{grad} f=\mathbf{\hat{x}}\frac{\partial f}{\partial x}+\mathbf{\hat{y}}\frac{\partial f}{\partial y}+ \mathbf{\hat{z}}\frac{\partial f}{\partial z}= \left(\frac{\partial f}{\partial x},\,\frac{\partial f}{\partial y},\,\frac{\partial f}{\partial z}\right). $$

A.5

Gradient vyjadřuje v každém bodě skalárního pole směr největšího růstu tohoto pole. Gradient vektoru (vektorového pole) $\vec{A}\,(x,\,y,\,z)$ je definován jako tenzor 2. řádu ve tvaru

$$ \vec{\nabla}\vec{A}=\text{grad}\vec{A}=\left(\mathbf{\hat{x}}\frac{\partial}{\partial x}+\mathbf{\hat{y}}\frac{\partial}{\partial y}+ \mathbf{\hat{z}}\frac{\partial}{\partial z}\right)\left(A_x\mathbf{\hat{x}}+A_y\mathbf{\hat{y}}+A_z\mathbf{\hat{z}}\right). $$

A.6

Protože se jedná o tzv. tenzorový součin, kdy se jednotlivé vektory báze násobí jako matice, z nichž první je sloupcová a druhá řádková, je třeba pro určení prvků tenzoru zachovat jejich pořadí. Pomocí maticového formalismu můžeme tenzor gradientu vektorového pole zapsat jako

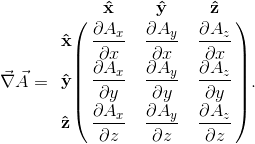A.7
Divergence vektoru (vektorového pole) $\vec{A}\,(x,\,y,\,z)$ je definována jako skalár (skalární pole)

$$ \vec{\nabla}\cdot\vec{A}=\text{div}\vec{A}=\mathbf{\hat{x}}\cdot\mathbf{\hat{x}}\,\frac{\partial A_x}{\partial x}+ \mathbf{\hat{y}}\cdot\mathbf{\hat{y}}\,\frac{\partial A_y}{\partial y}+\mathbf{\hat{z}}\cdot\mathbf{\hat{z}}\frac{\partial A_z}{\partial z}= \frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z}. $$

A.8

Divergenci vektoru lze v ortogonálních soustavách rovněž chápat jako stopu tenzoru gradientu vektorového pole. V obecných ortogonálních souřadnicích může být zapsána ve formě

$$ \begin{gather} \vec{\nabla}\cdot\vec{A}=\left[\frac{\partial}{\partial x_j}(h^kA^k)+\Gamma_{jl}^kh^lA^l\right]\delta_j^k=\frac{\partial}{\partial x_j}(h^jA^j)+\Gamma_{jl}^jh^lA^l. \end{gather} $$

A.9

S využitím rovnice 2.51 lze tento výraz přepsat rovněž do tvaru

$$ \begin{gather} \vec{\nabla}\cdot\vec{A}=\left[\frac{\partial}{\partial x_j}(h_kA_k)-\Gamma_{jk}^lh_lA_l\right]\delta_{jk}=\frac{\partial}{\partial x_j}(h_jA_j)-\Gamma_{jj}^lh_lA_l. \end{gather} $$

A.10

Členy $h_i$ jsou tzv. Laméovy koeficienty (často také nazývané škálovací faktory, nezaměňovat se stejnojmennými Laméovými koeficienty v mechanice kontinua), pojmenované po francouzském matematikovi Gabrieli Lamé, kde v příslušném metrickém tenzoru platí

$$ h_ih_i=g_{ii},\quad h^ih^i=g^{ii} $$

A.11

(proto nyní uvažujeme jen ortogonální soustavy, jejichž metrické tenzory mají nenulové prvky pouze na hlavní diagonále). Výraz $\Gamma_{jk}^{l}$ je tzv. Christoffelův symbol (pojmenovaný po německém matematikovi a fyzikovi Elwin Bruno Christoffelovi), definující tzv. členy křivosti v křivočarých souřadných soustavách,

$$ \Gamma_{jk}^{l}=\frac{1}{2}g^{lm}\left(\frac{\partial g_{km}}{\partial x_j}+\frac{\partial g_{jm}}{\partial x_k}- \frac{\partial g_{jk}}{\partial x_m}\right), $$

A.12

kde indexy $l,\,m$ jsou tzv. volné indexy, které mohou kdykoli nabývat kterékoli z hodnot $1,2,3$. Explicitní výraz pro divergenci vektoru v obecné ortogonální soustavě lze zapsat formou

$$ \vec{\nabla}\cdot\vec{A}=\frac{1}{h_ih_jh_k}\left[\frac{\partial}{\partial x_i}\left(h_jh_kA_i\right)+\frac{\partial}{\partial x_j}\left(h_kh_iA_j\right)+ \frac{\partial}{\partial x_k}\left(h_ih_jA_k\right)\right], $$

A.13

Ta je zcela ekvivalentní kompaktnější formě zápisu,

$$ \vec{\nabla}\cdot\vec{A}=\frac{1}{\sqrt{g}}\frac{\partial}{\partial x_i}\left(h_jh_kA_i\right)\Big|_{i\ne j\ne k}=\frac{1}{\sqrt{g}}\frac{\partial}{\partial x_i}\left(\sqrt{g}\,h^i\!A^i\right). $$

A.14

Složky $h^i\!A^i$ (v literatuře se většinou zkráceně uvádí pouze $A^i$) vektoru $\vec{A}$ odpovídají (viz rovnice 2.51) $h^i\!A^i=g^{ij}(h_jA_j)$ a $g$ je determinant metrického tenzoru, který je identický s druhou mocninou příslušného Jakobiánu souřadnicové transformace. Platí tedy

$$ \sqrt{\left|\det g_{ij}\right|}=J,\,\,\,\sqrt{\left|\det g^{ij}\right|}=J^{-1}. $$

A.15

Obecně také platí, že divergencí tenzoru řádu $n$ je tenzor řádu $n-1$, divergencí tenzoru druhého řádu tak bude vektor. Kompaktní forma zápisu divergence tenzoru 2. řádu bude mít tvar

$$ \nabla_jA^{ij}=A_i, $$

A.16

její explicitní zápis v kartézském systému (prakticky se jedná o maticové násobení vektoru s transponovanou maticí; při skalárním součinu dvou vektorů se také jedná o maticové násobení dvou vektorů, kdy druhý z vektorů je transponovaný, tedy sloupcový) bude vypadat

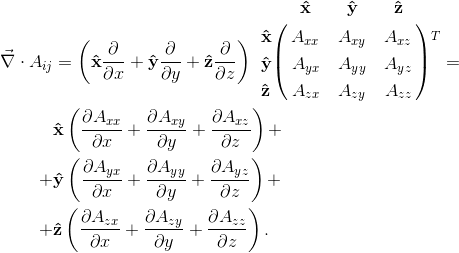A.17
Rotací vektoru (vektorového pole) $\vec{A}\,(x,\,y,\,z)$ v kartézské soustavě nazýváme vektor

$$ \vec\nabla\times\vec{A}=\mathbf{\hat{x}}\left(\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z}\right)+ \mathbf{\hat{y}}\left(\frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x}\right)+ \mathbf{\hat{z}}\left(\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\right). $$

A.18

Obecný výraz pro vektor rotace $\vec\nabla\times\vec{A}$ vektoru $\vec{A}$ v libovolné ortogonální souřadné soustavě lze definovat způsobem

$$ \vec\nabla\times\vec{A}=\epsilon_{ijk}\,\frac{1}{h_jh_k}\left[\nabla_j(h_kA_k)\right]\mathbf{\hat{x}}_i= \epsilon_{ijk}\,\frac{1}{h_jh_k}\left[\frac{\partial}{\partial x_j}(h_kA_k)-\Gamma_{jk}^lh_lA_l\right]\mathbf{\hat{x}}_i. $$

A.19

V rovnici A.19 výraz $\epsilon_{ijk}$ (kde všechny tři indexy $i,j,k$ mohou odpovídat postupně všem třem souřadnicovým směrům) odpovídá antisymetrickému, (tzv. Levi-Civitovu, viz rovnice 2.42) symbolu, který nabývá hodnoty $1$ pro sudé permutace indexů, $-1$ pro liché permutace indexů.

Díky symetrii indexů ve složkách vektoru rotace a díky úplné antisymetričnosti Levi-Civitova $\epsilon$-symbolu, se výrazy $\Gamma_{jk}^lA_l$ v rovnici A.19 vyruší, celý výraz se tak zjednoduší do podoby

$$ \vec\nabla\times\vec{A}=\epsilon_{ijk}\,\frac{1}{h_jh_k}\left[\frac{\partial}{\partial x_j}(h_kA_k)\right]\mathbf{\hat{x}}_i. $$

A.20

V kartézské soustavě, kde $h_1,h_2,h_3=1$, bude rovnice A.20 odpovídat rovnici A.18. Zapíšeme-li vektor rotace znovu po složkách, dostaneme

$$ \vec\nabla\times\vec{A}=\left(\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z},\, \frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x},\,\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\right).$$

A.21
Laplacián (Laplaceův operátor) je definován jako divergence gradientu, tedy $\vec{\nabla}\cdot\vec{\nabla}$ (používá se pro něj symbol $\Delta$), jedná se tedy o skalární operátor, který může působit na skalární funkce, vektory (po jednotlivých složkách), tenzory (po jednotlivých prvcích), aniž by měnil jejich řád (t.j. skalár zůstává skalárem, vektor vektorem, atd.). V kartézské soustavě má laplacián zcela jednoduchý tvar: analogicky k rovnici A.8, kde složky vektoru $\vec{A}$ nahradíme složkami vektoru gradientu, můžeme psát

$$ \begin{aligned} \Delta &=\vec{\nabla}\cdot\vec{\nabla}=\text{div}\,\text{grad}\! = \\ &= \mathbf{\hat{x}}\cdot\frac{\partial}{\partial x}\left(\mathbf{\hat{x}}\frac{\partial}{\partial x}\right)+ \mathbf{\hat{y}}\cdot\frac{\partial}{\partial y}\left(\mathbf{\hat{y}}\frac{\partial}{\partial y}\right)+ \mathbf{\hat{z}}\cdot\frac{\partial}{\partial z}\left(\mathbf{\hat{z}}\frac{\partial}{\partial z}\right)=\\ &=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}. \end{aligned} $$

A.22

nahoru

A.1.2 Plochy, objemy

Označme $S_k$ plochu s konstantní hodnotou souřadnice $x_k$, ohraničenou souřadnicovými křivkami $x_i,x_i+\Delta x_i,x_j,x_j+\Delta x_j$. V kartézské soustavě půjde např. o plochu s konstantní hodnotou $z=z_0$, ohraničenou přímkami $x=x_0,x=x_0+\Delta x,y=y_0,y=y_0+\Delta y$. Výpočet velikosti takové plochy je zde samozřejmě zcela triviální, půjde o obdélník (čtverec) s obsahem $\Delta x\Delta y$. Obecný vztah pro výpočet velikosti takové plochy bude mít ovšem tvar

$$ S_k=\int\limits_{x_{0i}}^{x_{0i}+\Delta x_i}\int\limits_{x_{0j}}^{x_{0j}+\Delta x_j}J^\prime_{ij}\,\text{d} x_i\,\text{d} x_j, $$

A.23

kde $J^\prime_{ij}$ je druhá odmocnina absolutní hodnoty determinantu příslušné submatice metrického tenzoru. V uvedeném případě by se jednalo o determinant $J^\prime_{ij}=\sqrt{|g_{ii}g_{jj}-g_{ij}g_{ji}|}$ (v případě ortogonálního souřadného systému bude determinant uvedených submatic sám o sobě kladný, pokud použijeme sudé permutace indexů a nediagonální členy dané submatice budou nulové). Integrand rovnice A.23 definujeme jako elementární plochu $\text{d} S_k=J^\prime_{ij}\,\text{d} x_i\,\text{d} x_j$. V kartézské soustavě budou zjevně determinanty všech tří submatic $J^\prime_{ij}=1$. Dále, označíme-li $V$ objem prostoru, vymezeného plochami s konstantními souřadnicemi $x_i,x_i+\Delta x_i,x_j,x_j+\Delta x_j,x_k,x_k+\Delta x_k$, obecný vztah pro výpočet velikosti takového objemu bude mít tvar

$$ V=\int\limits_{x_{0i}}^{x_{0i}+\Delta x_i}\int\limits_{x_{0j}}^{x_{0j}+\Delta x_j}\int\limits_{x_{0k}}^{x_{0k}+\Delta x_k} J\,\text{d} x_i\,\text{d} x_j\,\text{d} x_k, $$

A.24

kde $J$ je druhá odmocnina absolutní hodnoty determinantu metrického tenzoru (Jakobián – viz rovnice A.15). Integrand rovnice A.24 vyjadřuje elementární objem $\text{d} V=J\,\text{d} x_i\,\text{d} x_j\,\text{d} x_k$. V kartézské soustavě opět $J=1$, vymezený prostor bude mít tvar pravoúhlého kvádru o objemu $\Delta x\Delta y\Delta z$.

nahoru

A.1.3 Vektory polohy, rychlosti a zrychlení

V kartézské soustavě je zápis vektorů velmi jednoduchý, polohový vektor $\vec{r}$, vektor rychlosti $\vec{v}$ a vektor zrychlení $\vec{a}$ budou mít postupně tvar,

$$\vec{r}=x\mathbf{\hat{x}}+y\mathbf{\hat{y}}+z\mathbf{\hat{z}}=(x,y,z), $$

A.25

$$\vec{v}=\frac{\text{d}\vec{r}}{\text{d} t}=\dot{x}\mathbf{\hat{x}}+\dot{y}\mathbf{\hat{y}}+\dot{z}\mathbf{\hat{z}}= v_x\mathbf{\hat{x}}+v_y\mathbf{\hat{y}}+v_z\mathbf{\hat{z}}=(v_x,v_y,v_z), $$

A.26

$$ \vec{a}=\frac{\text{d}\vec{v}}{\text{d} t}=\ddot{x}\mathbf{\hat{x}}+\ddot{y}\mathbf{\hat{y}}+\ddot{z}\mathbf{\hat{z}}= a_x\mathbf{\hat{x}}+a_y\mathbf{\hat{y}}+a_z\mathbf{\hat{z}}=(a_x,a_y,a_z), $$

A.27

kde $\dot x=\text{d} x/\text{d} t$, $\dot y=\text{d} y/\text{d} t$ a $\dot z=\text{d} z/\text{d} t$.