A.3 Kulová soustava

Kulová soustava je vhodná pro popis jevů s centrální symetrií, jako jsou např. fyzikální pole, tvořená hmotnými body, astronomickými tělesy, atd. Mimo jiné se implicitně používá také v kartografii, kde soustava poledníků a rovnoběžek je vlastně soustava azimutálních a sférických úhlových souřadnic (viz dále). Zde je ovšem sférický úhel počítán jiným způsobem, v matematické konvenci roste od $0$ do $\pi$, v kartografické konvenci roste od $-\pi/2$ do $\pi/2$, navíc vopačném smyslu vůči směru nárůstu azimutální souřadnice.

Souřadnicové směry jsou: $r$ – vzdálenost od středu kulové symetrie, $\theta$ – sférický úhel, $\phi$ – azimutální úhel. Převod z kulové do kartézské soustavy je dán vztahy

$$ x=r\sin\theta\cos\phi,\quad y=r\sin\theta\sin\phi,\quad z=r\cos\theta.$$

A.55

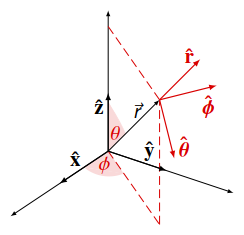
Obrázek A.2: Vzájemná poloha jednotkových bázových vektorů kartézské a kulové souřadné soustavy (viz rovnice A.57 a A.60).

Pro zpětnou transformaci z kartézské do kulové soustavy platí Uvedené vztahy pro $\theta$ a $\phi$ neuvádí jednoznačné výrazy pro všechny kvadranty, viz rovnice A.29. Pro exaktní popis doporučuji např.: Musilová & Musilová (2006).

$$ r=\sqrt{x^2+y^2+z^2},\quad \theta=\arccos\dfrac{z}{\sqrt{x^2+y^2+z^2}},\quad \phi=\text{arctg}\,\dfrac{y}{x}. $$

A.56

Analogicky k rovnici A.30 budou mít jednotkové vektory kulové báze v kartézské soustavě tvar (viz pravidla pro sčítání vektorů)

$$ \begin{aligned} \mathbf{\hat{\boldsymbol{r}}}&=\mathbf{\hat{x}}\sin\theta\cos\phi+ \mathbf{\hat{y}}\sin\theta\sin\phi+\mathbf{\hat{z}}\cos\theta= (\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta),\\ \mathbf{\hat{\boldsymbol{\theta}}}&=\mathbf{\hat{x}}\cos\theta\cos\phi+ \mathbf{\hat{y}}\cos\theta\sin\phi-\mathbf{\hat{z}}\sin\theta= (\cos\theta\cos\phi,\cos\theta\sin\phi,-\sin\theta),\\ \mathbf{\hat{\boldsymbol{\phi}}}&=-\mathbf{\hat{x}}\sin\phi+\mathbf{\hat{y}}\cos\phi= (-\sin\phi,\cos\phi,0). \end{aligned} $$

A.57

V kulové soustavě není žádný z vektorů báze konstantní. Derivace bázových vektorů ve směru jednotlivých souřadnicových os budou (z rovnice A.57)

$$ \begin{aligned} &\dfrac{\partial\mathbf{\hat{\boldsymbol{r}}}}{\partial r}=0, &&\dfrac{\partial\mathbf{\hat{\boldsymbol{r}}}}{\partial{\theta}}=\mathbf{\hat{\boldsymbol{\theta}}}, &&\dfrac{\partial\mathbf{\hat{\boldsymbol{r}}}}{\partial{\phi}}=\mathbf{\hat{\boldsymbol{\phi}}}\sin\theta,\\ &\dfrac{\partial\mathbf{\hat{\boldsymbol\theta}}}{\partial r}=0, &&\dfrac{\partial\mathbf{\hat{\boldsymbol\theta}}}{\partial\theta}=-\mathbf{\hat{\boldsymbol{r}}}, &&\dfrac{\partial\mathbf{\hat{\boldsymbol{\theta}}}}{\partial{\phi}}=\mathbf{\hat{\boldsymbol{\phi}}}\cos\theta,\\ &\dfrac{\partial\mathbf{\hat{\boldsymbol\phi}}}{\partial r}=0, &&\dfrac{\partial\mathbf{\hat{\boldsymbol\phi}}}{\partial\theta}=0, &&\dfrac{\partial\mathbf{\hat{\boldsymbol{\phi}}}}{\partial{\phi}}= -\mathbf{\hat{\boldsymbol{r}}}\sin\theta-\mathbf{\hat{\boldsymbol{\theta}}}\cos\theta. \end{aligned} $$

A.58

Časové derivace bázových vektorů budou

$$ \begin{aligned} \dfrac{\partial\mathbf{\hat{\boldsymbol{r}}}}{\partial t}= \dfrac{\partial\mathbf{\hat{\boldsymbol{r}}}}{\partial\theta}\dfrac{\partial\theta}{\partial t}+ \dfrac{\partial\mathbf{\hat{\boldsymbol{r}}}}{\partial\phi}\dfrac{\partial\phi}{\partial t} &=\mathbf{\hat{\boldsymbol{\theta}}}\dot{\theta}+\mathbf{\hat{\boldsymbol{\phi}}}\dot{\phi}\sin\theta,\\ \dfrac{\partial\mathbf{\hat{\boldsymbol{\theta}}}}{\partial t}= \dfrac{\partial\mathbf{\hat{\boldsymbol{\theta}}}}{\partial\theta}\dfrac{\partial\theta}{\partial t}+ \dfrac{\partial\mathbf{\hat{\boldsymbol{\theta}}}}{\partial\phi}\dfrac{\partial\phi}{\partial t} &=-\mathbf{\hat{\boldsymbol{r}}}\dot{\theta}+\mathbf{\hat{\boldsymbol{\phi}}}\dot{\phi}\cos\theta,\\ \dfrac{\partial\mathbf{\hat{\boldsymbol{\phi}}}}{\partial t}= \dfrac{\partial\mathbf{\hat{\boldsymbol{\phi}}}}{\partial\phi}\dfrac{\partial\phi}{\partial t} &=-\mathbf{\hat{\boldsymbol{r}}}\dot{\phi}\sin\theta-\mathbf{\hat{\boldsymbol{\theta}}}\dot{\phi}\cos\theta. \end{aligned} $$

A.59

Zpětnou transformací jednotkových bázových vektorů (viz rovnice A.57) dostáváme

$$ \begin{aligned} \mathbf{\hat{x}}&=\mathbf{\hat{\boldsymbol{r}}}\sin\theta\cos\phi+ \mathbf{\hat{\boldsymbol{\theta}}}\cos\theta\cos\phi-\mathbf{\hat{\boldsymbol{\phi}}}\sin\phi,\\ \mathbf{\hat{y}}&=\mathbf{\hat{\boldsymbol{r}}}\sin\theta\sin\phi+ \mathbf{\hat{\boldsymbol{\theta}}}\cos\theta\sin\phi+\mathbf{\hat{\boldsymbol{\phi}}}\cos\phi,\\ \mathbf{\hat{z}}&=\mathbf{\hat{\boldsymbol{r}}}\cos\theta-\mathbf{\hat{\boldsymbol{\theta}}}\sin\theta. \end{aligned} $$

A.60

Metrickou formu pro kulovou soustavu dostaneme diferencováním rovnice A.55,

$$ \begin{aligned} \text{d} x&=\text{d} r\sin\theta\cos\phi+r\cos\theta\cos\phi\,\text{d}\theta- r\sin\theta\sin\phi\,\text{d}\phi,\\ \text{d} y&=\text{d} r\sin\theta\sin\phi+r\cos\theta\sin\phi\,\text{d}\theta+ r\sin\theta\cos\phi\,\text{d}\phi,\\ \text{d} z&=\text{d} r\cos\theta-r\sin\theta\,\text{d}\theta, \end{aligned} $$

A.61

dosazením do rovnice A.2 dostáváme kulovou metrickou formu

$$ \text{d} s^2=\text{d} r^2+r^2\,\text{d}\theta^2+r^2\sin^2\theta\,\text{d}\phi^2. $$

A.62

Kovariantní ($g_{ij}$) i kontravariantní ($g^{ij}$) metrický tenzor a také (viz rovnice A.11) příslušné Laméovy koeficienty kulové souřadné soustavy budou,

$$ \begin{aligned} g_{ij}= \begin{pmatrix} 1 & 0 & 0\\0 & r^2 & 0\\0 & 0 & r^2\sin^2\theta \end{pmatrix},\quad g^{ij}= \begin{pmatrix} 1 & 0 & 0\\0 & {\dfrac{1}{r^2}} & 0\\0 & 0 & {\dfrac{1}{r^2\sin^2\theta}} \end{pmatrix},\\ h_r=1,\,h_\theta=r,\,h_\phi=r\sin\theta. \end{aligned} $$

A.63

Podle rovnice A.12 odvodíme nenulové Christoffelovy symboly kulové metriky,

$$ \begin{aligned} \Gamma_{\theta\theta}^r &=-r,\,\Gamma_{\theta r}^{\theta}\,(\Gamma_{r\theta}^{\theta})= \Gamma_{\phi r}^{\phi}\,(\Gamma_{r\phi}^{\phi})=\dfrac{1}{r},\\ \Gamma_{\phi\phi}^r&=-r\sin^2\theta,\, \Gamma_{\phi\phi}^\theta=-\sin\theta\cos\theta,\,\Gamma_{\phi\theta}^\phi\,(\Gamma_{\theta\phi}^\phi)=\,\text{cotg}\,\theta. \end{aligned} $$

A.64

nahoru

A.3.1 Diferenciální operátory

Gradient skalární funkce $f=f\,(\rho,\,\phi,\,z)$ v kulové soustavě odvodíme podle rovnice A.5, kam za jednotkové bázové vektory dosadíme výrazy z rovnice A.60 a jednotlivé složky gradientu rozvineme řetězovým pravidlem pro derivace. Po rozepsání dostáváme

$$ \begin{aligned} \vec{\nabla}f=&\left(\mathbf{\hat{\boldsymbol{r}}}\sin\theta\cos\phi+ \mathbf{\hat{\boldsymbol{\theta}}}\cos\theta\cos\phi-\mathbf{\hat{\boldsymbol{\phi}}}\sin\phi\right) \left(\dfrac{\partial f}{\partial r}\dfrac{\partial r}{\partial x}+\dfrac{\partial f}{\partial\theta}\dfrac{\partial\theta}{\partial x} +\dfrac{\partial f}{\partial\phi}\dfrac{\partial\phi}{\partial x}\right)+\\+ &\left(\mathbf{\hat{\boldsymbol{r}}}\sin\theta\sin\phi+ \mathbf{\hat{\boldsymbol{\theta}}}\cos\theta\sin\phi+\mathbf{\hat{\boldsymbol{\phi}}}\cos\phi\right) \left(\dfrac{\partial f}{\partial r}\dfrac{\partial r}{\partial y}+\dfrac{\partial f}{\partial\theta}\dfrac{\partial\theta}{\partial y}+ \dfrac{\partial f}{\partial\phi}\dfrac{\partial\phi}{\partial y}\right)+\\ +&\left(\mathbf{\hat{\boldsymbol{r}}}\cos\theta-\mathbf{\hat{\boldsymbol{\theta}}}\sin\theta\right) \left(\dfrac{\partial f}{\partial r}\dfrac{\partial r}{\partial z}+\dfrac{\partial f}{\partial\theta}\dfrac{\partial\theta}{\partial z} \right). \end{aligned} $$

A.65

Jednotlivé parciální derivace vypočítáme z rovnice A.56,

$$ \begin{aligned} &\dfrac{\partial r}{\partial x}=\dfrac{x}{\sqrt{x^2+y^2+z^2}}=\sin\theta\cos\phi, \\ &\dfrac{\partial\theta}{\partial x}=\dfrac{xz},{\sqrt{x^2+y^2}\left(x^2+y^2+z^2\right)}=\dfrac{\cos\theta\cos\phi}{r},\\ &\dfrac{\partial r}{\partial y}=\dfrac{y}{\sqrt{x^2+y^2+z^2}}=\sin\theta\sin\phi, \\ &\dfrac{\partial\theta}{\partial y}=\dfrac{yz}{\sqrt{x^2+y^2}\left(x^2+y^2+z^2\right)}=\dfrac{\cos\theta\sin\phi}{r},\\ &\dfrac{\partial r}{\partial z}=\dfrac{z}{\sqrt{x^2+y^2+z^2}}=\cos\theta, \\ &\dfrac{\partial\theta}{\partial z}=-\dfrac{\sqrt{x^2+y^2}}{x^2+y^2+z^2}=-\dfrac{\sin\theta}{r},\\ &\dfrac{\partial\phi}{\partial x}=-\dfrac{y}{x^2+y^2}=-\dfrac{\sin\phi}{r\sin\theta},\\ &\dfrac{\partial\phi}{\partial y}=\dfrac{x}{x^2+y^2}=\dfrac{\cos\phi}{r\sin\theta}. \end{aligned} $$

A.66

Po dosazení a úpravě dostaneme výslednou podobu gradientu

$$ \vec{\nabla}f=\mathbf{\hat{\boldsymbol{r}}}\dfrac{\partial f}{\partial r}+ \mathbf{\hat{\boldsymbol{\theta}}}\dfrac{1}{r}\dfrac{\partial f}{\partial\theta}+ \mathbf{\hat{\boldsymbol{\phi}}}\dfrac{1}{r\sin\theta}\dfrac{\partial f}{\partial\phi}= \left(\dfrac{\partial f}{\partial r},\,\dfrac{1}{r}\dfrac{\partial f}{\partial\theta},\, \dfrac{1}{r\sin\theta}\dfrac{\partial f}{\partial\phi}\right). $$

A.67

Opět zde za jednotkové vektory kulové báze nedosazujeme jejich složky z rovnice A.57, kde jsme je viděli ze soustavy kartézské. Analogicky k rovnici A.6 (tenzorový součin) a s použitím rovnice A.67 je potom gradient vektorového pole $\vec{A}\,(r,\,\theta,\,\phi)$ v kulové soustavě definován jako tenzor 2. řádu ve tvaru

$$ \vec{\nabla}\vec{A}=\left(\mathbf{\hat{\boldsymbol{r}}}\dfrac{\partial}{\partial r}+ \mathbf{\hat{\boldsymbol{\theta}}}\dfrac{1}{r}\dfrac{\partial}{\partial\theta}+ \mathbf{\hat{\boldsymbol{\phi}}}\dfrac{1}{r\sin\theta}\dfrac{\partial}{\partial\phi}\right) \left(A_r\mathbf{\hat{\boldsymbol{r}}}+A_{\theta}\mathbf{\hat{\boldsymbol{\theta}}}+A_\phi\mathbf{\hat{\boldsymbol{\phi}}}\right). $$

A.68

Na rozdíl od válcové soustavy zde operátor gradientu již působí na všechny jednotkové bázové vektory (jejich derivace – viz rovnice A.58). Pomocí maticového formalismu můžeme tenzor gradientu vektorového pole v kulové soustavě zapsat

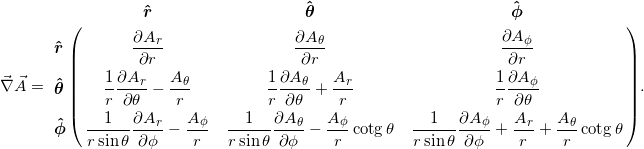A.69

Stejného výsledku docílíme i v tomto případě např. s použitím formalismu Christoffelových symbolů (viz rovnice A.37) dle obecného vztahu A.43, tento postup lze ovšem použít pouze pro ortogonální souřadné soustavy, zatímco postup podle rovnice A.68 platí zcela obecně.
Divergence vektoru (vektorového pole) $\vec{A}\,(r,\,\theta,\,\phi)$ je v kulových souřadnicích ve smyslu rovnice A.68, analogicky k rovnici A.8, definována jako skalár (skalární pole)

$$ \begin{aligned} \vec{\nabla}\cdot\vec{A}=\mathbf{\hat{\boldsymbol{r}}}\cdot\mathbf{\hat{\boldsymbol{r}}}\, \dfrac{\partial A_r}{\partial r}+ \mathbf{\hat{\boldsymbol{\theta}}}\cdot\mathbf{\hat{\boldsymbol{\theta}}} \left(\dfrac{1}{r}\dfrac{\partial A_{\theta}}{\partial\theta}+\dfrac{A_r}{r}\right) + \\ +\mathbf{\hat{\boldsymbol{\phi}}}\cdot\mathbf{\hat{\boldsymbol{\phi}}} \left(\dfrac{1}{r\sin\theta}\dfrac{\partial A_\phi}{\partial\phi}+\dfrac{A_r}{r}+ \dfrac{A_\theta}{r}\,\text{cotg}\,\theta\right)=\\ =\dfrac{1}{r^2}\dfrac{\partial}{\partial r}\left(r^2A_r\right)+ \dfrac{1}{r\sin\theta}\dfrac{\partial}{\partial\theta}\left(\sin\theta A_{\theta}\right)+ \dfrac{1}{r\sin\theta}\dfrac{\partial A_{\phi}}{\partial\phi}. \end{aligned} $$

A.70

Porovnáním s rovnicí A.69 opět vidíme, že divergence je stopou tenzoru gradientu vektorového pole.
Rotaci vektoru (vektorového pole) $\vec{A}\,(r,\,\theta,\,\phi)$ v kulové soustavě, kde $h_r=1,\,h_{\theta}=r,\,h_\phi=r\sin\theta$, odvodíme podle rovnice A.20, v tomto případě dostaneme

$$ \begin{aligned} \vec\nabla\times\vec{A}=\dfrac{1}{r\sin\theta} \left[\dfrac{\partial}{\partial\theta}\left(\sin\theta\,A_\phi\right)- \dfrac{\partial A_\theta}{\partial\phi}\right]\mathbf{\hat{\boldsymbol{r}}}+ \dfrac{1}{r}\left[\dfrac{1}{\sin\theta}\dfrac{\partial A_r}{\partial\phi}- \dfrac{\partial}{\partial r}\left(rA_\phi\right)\right]\mathbf{\hat{\boldsymbol{\theta}}}\\ +\,\dfrac{1}{r}\left[\dfrac{\partial}{\partial r}\left(rA_\theta\right)-\dfrac{\partial A_r}{\partial\theta}\right]\mathbf{\hat{\boldsymbol{\phi}}}. \end{aligned}$$

A.71
Laplacián odvodíme (viz rovnice A.22), nahradíme-li v rovnici divergence A.70 složky vektoru $\vec{A}$ odpovídajícími složkami vektoru gradientu z rovnice A.67, výsledný tvar, zapsaný v kompaktní formě bude

$$ \Delta=\vec{\nabla}\cdot\vec{\nabla}=\dfrac{1}{r^2}\dfrac{\partial}{\partial r}\left(r^2\dfrac{\partial}{\partial r}\right)+ \dfrac{1}{r^2\sin\theta}\dfrac{\partial}{\partial\theta}\left(\sin\theta\dfrac{\partial}{\partial\theta}\right)+ \dfrac{1}{r^2\sin^2\theta}\dfrac{\partial^2}{\partial\phi^2}. $$

A.72

nahoru

A.3.2 Plochy, objemy

Stejně jako v předchozích soustavách označme $S_k$ plochu s konstantní hodnotou souřadnice $x_k$, ohraničenou souřadnicovými křivkami $x_i,x_i+\Delta x_i,x_j,x_j+\Delta x_j$. V kulové soustavě půjde např. o plochu s konstantní hodnotou $r=r_0$, ohraničenou dvojicemi křivek (kružnicemi) sesouřadnicemi $\theta=\theta_1,\theta=\theta_2$ a $\phi=\phi_1,\phi=\phi_2$. Výpočet velikosti takové plochy již zde není vůbec triviální, půjde o část plochy s dvojí křivostí, ohraničenou dvěma rozbíhajícími se souřadnicovými plochami (v nichž leží křivky se souřadnicemi $\phi=\phi_1,\,\phi=\phi_2$) a dvěma kružnicemi se středy na společné ose, avšak ležícími v různých rovinách, kolmých na tuto osu (křivky se souřadnicemi $\theta=\theta_1,\theta=\theta_2$). Pokud budeme uvažovat jinou plochu, např. s konstantní souřadnicí $\phi=\phi_0$, ohraničenou souřadnicovými plochami $\theta=\theta_1,\theta=\theta_2,r=r_1,r=r_2$, půjde o část kruhové výseče, omezené dvěma soustřednými kružnicemi. Při výpočtech velikostí těchto ploch vyjdeme opět z rovnice A.23 a z rovnice A.63, tedy

$$ \begin{aligned} S_r&=\int\limits_{\theta_1}^{\theta_2}\int\limits_{\phi_1}^{\phi_2}\sqrt{g_{\theta\theta}\,g_{\phi\phi}}\,\text{d}\theta\,\text{d}\phi= \int\limits_{\theta_1}^{\theta_2}\int\limits_{\phi_1}^{\phi_2}r^2\sin\theta\,\text{d}\theta\,\text{d}\phi= r^2\left(\cos\theta_1-\cos\theta_2\right)\Delta\phi,\\ S_\theta&=\int\limits_{\phi_1}^{\phi_2}\int\limits_{r_1}^{r_2}\sqrt{g_{\phi\phi}\,g_{rr}}\,\text{d}\phi\,\text{d} r= \int\limits_{\phi_1}^{\phi_2}\int\limits_{r_1}^{r_2}r\sin\theta\,\text{d}\phi\,\text{d} r= \dfrac{r_2^2-r_1^2}{2}\sin\theta\Delta\phi,\\ S_\phi&=\int\limits_{r_1}^{r_2}\int\limits_{\theta_1}^{\theta_2}\sqrt{g_{rr}\,g_{\theta\theta}}\,\text{d} r\,\text{d}\theta= \int\limits_{r_1}^{r_2}\int\limits_{\theta_1}^{\theta_2}r\,\text{d} r\,\text{d} \theta=\dfrac{r_2^2-r_1^2}{2}\Delta\theta. \end{aligned} $$

A.73

V kulovém, tedy opět ortogonálním souřadném systému, budou všechny nediagonální členy submatic $J^\prime_{ij}$ (viz rovnice A.23) nulové. Označme tradičně $V$ objem prostoru, vymezeného souřadnicovými plochami s konstantními souřadnicemi $r_1,r_2,\theta_1,\theta_2,\phi_1,\phi_2$, tvar takového útvaru odpovídá v tomto případě průniku jehlanu s koncentrickou sférickou mezivrstvou (mezikoulím), vztah pro výpočet velikosti takového objemu bude mít dle rovnice A.24 tvar

$$ V=\int\limits_{r_1}^{r_2}\int\limits_{\theta_1}^{\theta_2}\int\limits_{\phi_1}^{\phi_2} r^2\sin\theta\,\text{d} r\,\text{d}\theta\,\text{d}\phi= \dfrac{r_2^3-r_1^3}{3}\left(\cos\theta_1-\cos\theta_2\right)\Delta\phi. $$

A.74

V ortogonálním kulovém souřadném systému obdobně jako ve válcovém systému můžeme Jakobián $J$ stanovit jako ${\sqrt{g_{rr}\,g_{\theta\theta}\,g_{\phi\phi}}}=r^2\sin\theta$. Popsaná metoda umožní při odpovídajícím stanovení integračních mezí vypočítat v kulovém souřadném systému velikosti jakkoli složitějších útvarů

nahoru

A.3.3 Vektory polohy, rychlosti a zrychlení

Při popisu vektorů v kulové soustavě vyjdeme z jejich základního popisu v soustavě kartézské, zahrneme všechny rovnice pro derivace jednotkových vektorů i složek vektorů (rovnice A.55-A.60). Polohový vektor a vektor rychlosti v kulové soustavě budou

$$ \vec{r}=x\mathbf{\hat{x}}+y\mathbf{\hat{y}}+z\mathbf{\hat{z}}=r\mathbf{\hat{\boldsymbol{r}}},\quad \vec{v}=\dfrac{\text{d}\vec{r}}{\text{d} t}=\dfrac{\text{d}\left(r\mathbf{\hat{\boldsymbol{r}}}\right)}{\text{d} t}= \dot{r}\mathbf{\hat{\boldsymbol{r}}}+{r}\dot{\mathbf{\hat{\boldsymbol{r}}}}= \dot{r}\mathbf{\hat{\boldsymbol{r}}}+{r}\left(\dot{\theta}\mathbf{\hat{\boldsymbol{\theta}}}+ \dot{\phi}\mathbf{\hat{\boldsymbol{\phi}}}\sin\theta\right). $$

A.75

Tento závěr lze opět očekávat, uvědomíme-li si, že polohový vektor vychází z počátku souřadnic. Vektory rychlosti a zrychlení jsou zároveň definovány jako

$$ \vec{v}=v_r\mathbf{\hat{\boldsymbol{r}}}+ v_\theta\mathbf{\hat{\boldsymbol{\theta}}}+v_\phi\mathbf{\hat{\boldsymbol{\phi}}},\quad \vec{a}=\dfrac{\text{d}\vec{v}}{\text{d} t}=a_r\mathbf{\hat{\boldsymbol{r}}}+a_\theta\mathbf{\hat{\boldsymbol{\theta}}}+ a_\phi\mathbf{\hat{\boldsymbol{\phi}}}. $$

A.76

Derivováním rovnice A.75 podle času dostáváme jednotlivé složky vektoru zrychlení v kulové souřadné soustavě,

$$ \begin{align} a_r =\ddot{r}-r\dot{\theta}^2-r\dot{\phi}^2\sin^2\theta =\dfrac{\text{d}\,v_r}{\text{d}\,t}-r\dot{\theta}^2-r\dot{\phi}^2\sin^2\theta, \end{align} $$

A.77

$$ \begin{align} a_r =\ddot{r}-r\dot{\theta}^2-r\dot{\phi}^2\sin^2\theta =\dfrac{\text{d}\,v_r}{\text{d}\,t}-r\dot{\theta}^2-r\dot{\phi}^2\sin^2\theta, \end{align} $$

A.78

$$ \begin{align} a_\phi =r\ddot{\phi}\sin\theta+2\dot{r}\dot{\phi}\sin\theta+2r\dot{\theta}\dot{\phi}\cos\theta =\dfrac{\text{d}\,v_\phi}{\text{d}\,t}+\dot{r}\dot{\phi}\sin\theta+r\dot{\theta}\dot{\phi}\cos\theta, \end{align} $$

A.79

Protože $\text{d}/\text{d}\,t=\partial/\partial t+\vec{v}\cdot\vec{\nabla}$ (řetězové pravidlo pro derivování, v tomto případě pro parciální derivace $\vec{v}=\vec{v}(t,r,\theta,\phi)$), potom zrychlení, vyjádřené v kulové souřadné soustavě pomocí složek vektoru rychlosti bude

$ a_r=\dfrac{\partial v_r}{\partial t}+\underbrace{v_r\dfrac{\partial v_r}{\partial r}+ \dfrac{v_\theta}{r}\dfrac{\partial v_r}{\partial\theta} +\dfrac{v_\phi}{r\sin\theta}\dfrac{\partial v_r}{\partial\phi}}_{\left(\vec{v}\cdot\vec{\nabla}\right)v_r}- \dfrac{v_\theta^2+v_\phi^2}{r}, $

A.80

$ a_\theta=\dfrac{\partial v_\theta}{\partial t}+\underbrace{v_r\dfrac{\partial v_\theta}{\partial r}+ \dfrac{v_\theta}{r}\dfrac{\partial v_\theta}{\partial\theta} +\dfrac{v_\phi}{r\sin\theta}\dfrac{\partial v_\theta}{\partial\phi}}_{\left(\vec{v}\cdot\vec{\nabla}\right)v_\theta}+ \dfrac{v_r v_\theta}{r}-\dfrac{v^2_\phi\cot\theta}{r}, $

A.81

$ a_\phi=\dfrac{\partial v_\phi}{\partial t}+\underbrace{v_r\dfrac{\partial v_\phi}{\partial r}+ \dfrac{v_\theta}{r}\dfrac{\partial v_\phi}{\partial\theta} +\dfrac{v_\phi}{r\sin\theta}\dfrac{\partial v_\phi}{\partial\phi}}_{\left(\vec{v}\cdot\vec{\nabla}\right)v_\phi}+ \dfrac{v_r v_\phi}{r}+\dfrac{v_\theta v_\phi\cot\theta}{r}. $

A.82

Bylo by jistě možné popsat mnohem více podrobností, např. operace s vektory a tenzory v rámci popisovaných soustav, atd., zde jsou ukázány alespoň některé postupy spíše z praktického pohledu. V dalších odstavcích ukážeme stručně alespoň jednu neortogonální souřadnou soustavu, jejíž popis byl do jisté míry vyvolán tvorbou numerické výpočetní sítě pro hydrodynamické modelování konkrétního fyzikálního jevu.