A.2 Válcová soustava

Válcová soustava může být vhodná pro popis celé řady osově symetrických a rotačních jevů, např. elektrického a magnetického pole okolo přímých vodičů, vírů v tekutinách, galaxií, hvězdných disků, atd. Souřadnicové směry jsou: $\rho$ – vzdálenost od osy válcové symetrie, $\phi$ – azimutální úhel, $z$ – výška. Převod z válcové do kartézské soustavy je dán vztahy V dalším popisu budeme rozlišovat $\rho$ pro radiální válcovou souřadnici, $r$ pro radiální kulovou souřadnici. V případě jednotkových bázových vektorů budeme rozlišovat $\mathbf{\hat{\boldsymbol{\rho}}}$ pro válcovou souřadnici, $\mathbf{\hat{\boldsymbol{r}}}$ pro kulovou souřadnici. Nekonstantnost jednotkových vektorů válcové i kulové báze je rovněž zvýrazněna skloněným písmem, konstantní bázové vektory jsou zapsány stojatými písmeny.

$$ x=\rho\cos\phi,\quad y=\rho\sin\phi,\quad z=z. $$

A.28

Pro zpětnou transformaci z kartézské do válcové soustavy platí Pro vyčerpávající popis vztahu pro azimutální úhel $\phi$ doporučuji např.: Musilová & Musilová (2006).

$ \rho=\sqrt{x^2+y^2},\quad\phi=\text{arctg}\,\dfrac{y}{x}$ pro $x\neq 0$, případně $\phi=\arccos\dfrac{x}{\rho},\quad z=z$.

A.29

Obrazek — Obrázek A.1: Schéma vzájemné transformace jednotkových bázových vektorů kartézské a válcové souřadné soustavy (viz rovnice A.30 a A.33).

Vztah pro azimutální úhel $\phi$ je strukturovanější, výraz uvedený v rovnici A.29 platí jednoznačně pouze pro 1. kvadrant, $\phi\in\langle 0,\pi/2)$. Pro ostatní kvadranty je třeba vždy zvážit znaménka souřadnic $x$ a $y$, pokud např. $x<0\wedge y\geq 0$, jedná se o 2. kvadrant, atd.

Jednotkové vektory válcové báze budou mít v kartézské soustavě tvar (viz sčítání vektorů)

$$ \begin{align} \mathbf{\hat{\boldsymbol{\rho}}}&=\mathbf{\hat{x}}\cos\phi+\mathbf{\hat{y}}\sin\phi= (\cos\phi,\sin\phi,0),\\ \mathbf{\hat{\boldsymbol{\phi}}}&=-\mathbf{\hat{x}}\sin\phi+\mathbf{\hat{y}}\cos\phi= (-\sin\phi,\cos\phi,0),\\ \mathbf{\hat{z}}&=(0,0,1). \end{align}$$

A.30

Jediným konstantním bázovým vektorem bude vektor $\mathbf{\hat{z}}$, ostatní bázové vektory mění směr v závislosti na úhlu $\phi$. Nenulové derivace bázových vektorů ve směru souřadnicových os a nenulové časové derivace bázových vektorů budou (z rovnice A.30)

$$ \begin{align} &\dfrac{\partial\mathbf{\hat{\boldsymbol{\rho}}}}{\partial{\phi}}= (-\sin\phi,\cos\phi,0)=\mathbf{\hat{\boldsymbol{\phi}}},&& \dfrac{\partial\mathbf{\hat{\boldsymbol{\rho}}}}{\partial t}= \dfrac{\partial\mathbf{\hat{\boldsymbol{\rho}}}}{\partial\phi}\dfrac{\partial\phi}{\partial t}= \mathbf{\hat{\boldsymbol{\phi}}}\dot{\phi},\\ &\dfrac{\partial\mathbf{\hat{\boldsymbol\phi}}}{\partial\phi}=(-\cos\phi,-\sin\phi,0)=-\mathbf{\hat{\boldsymbol{\rho}}},&& \dfrac{\partial\mathbf{\hat{\boldsymbol{\phi}}}}{\partial t}= \dfrac{\partial\mathbf{\hat{\boldsymbol{\phi}}}}{\partial\phi}\dfrac{\partial\phi}{\partial t}=-\mathbf{\hat{\boldsymbol{\rho}}}\dot{\phi}. \end{align} $$

A.31

Pokud budeme derivovat jednotkové vektory válcové báze ve směru kartézských souřadnicových os, potom např. ve směru osy $x$ dostaneme

$$ \begin{align} \dfrac{\partial\mathbf{\hat{\boldsymbol{\rho}}}}{\partial x}&=\dfrac{\partial(\cos\phi,\sin\phi,\,0)}{\partial x}= \dfrac{\partial}{\partial x}\left(\dfrac{x}{\sqrt{x^2+y^2}},\dfrac{y}{\sqrt{x^2+y^2}},0\right)= -\mathbf{\hat{\boldsymbol{\phi}}}\,\dfrac{\sin\phi}{\rho},\\ \dfrac{\partial\mathbf{\hat{\boldsymbol{\phi}}}}{\partial x}&= \dfrac{\partial(-\sin\phi,\cos\phi,\,0)}{\partial x}= \mathbf{\hat{\boldsymbol{\rho}}}\,\dfrac{\sin\phi}{\rho}. \end{align} $$

A.32

Obdobně získáme derivace ve všech ostatních směrech. Zpětná transformace jednotkových bázových vektorů (viz rovnice A.30) bude

$$ \mathbf{\hat{x}}=\mathbf{\hat{\boldsymbol{\rho}}}\cos\phi-\mathbf{\hat{\boldsymbol{\phi}}}\sin\phi,\quad \mathbf{\hat{y}}=\mathbf{\hat{\boldsymbol{\rho}}}\sin\phi+\mathbf{\hat{\boldsymbol{\phi}}}\cos\phi,\quad \mathbf{\hat{z}}=\mathbf{\hat{z}}. $$

A.33

Metrickou formu pro válcovou soustavu snadno odvodíme, uvědomíme-li si, že vzdálenost dvou bodů v prostoru musí být nezávislá na volbě souřadného systému, tedy $\text{d} s^2$ z rovnice A.2 se musí pro všechny souřadné soustavy rovnat. Z rovnice A.28 dostaneme,

$$ \text{d} x=\text{d}\rho\cos\phi-\rho\sin\phi\,\text{d} \phi,\quad \text{d} y=\text{d}\rho\sin\phi+\rho\cos\phi\,\text{d} \phi,\quad \text{d} z=\text{d} z, $$

A.34

dosazením do rovnice A.2 dostáváme válcovou metrickou formu

$$ \text{d} s^2=\text{d}\rho^2+\rho^2\,\text{d}\phi^2+\text{d} z^2, $$

A.35

můžeme tedy napsat kovariantní ($g_{ij}$) i kontravariantní ($g^{ij}$) metrický tenzor a také (viz rovnice A.11) příslušné Laméovy koeficienty válcové souřadné soustavy,

$$ g_{ij}= \begin{pmatrix} 1 & 0 & 0\\0 & \rho^2 & 0\\0 & 0 & 1 \end{pmatrix},\quad g^{ij}= \begin{pmatrix} 1 & 0 & 0\\0 & {\dfrac{1}{\rho^2}} & 0\\0 & 0 & 1 \end{pmatrix},\quad h_\rho=1,\,h_\phi=\rho,\,h_z=1. $$

A.36

Nenulové Christoffelovy symboly válcové metriky z rovnice A.12 budou

$$ \Gamma_{\phi\phi}^\rho=-\rho,\,\Gamma_{\phi\rho}^{\phi}\,(\Gamma_{\rho\phi}^{\phi})=\dfrac{1}{\rho}. $$

A.37

nahoru

A.2.1 Diferenciální operátory

Gradient skalární funkce $f=f\,(\rho,\,\phi,\,z)$ ve válcové soustavě odvodíme z rovnice A.5, kam za jednotkové bázové vektory dosadíme výrazy z rovnice A.33 a jednotlivé složky gradientu rozvineme řetězovým pravidlem pro derivace. Po rozepsání dostáváme

$$ \begin{aligned} \vec{\nabla}f= &\left(\mathbf{\hat{\boldsymbol{\rho}}}\cos\phi-\mathbf{\hat{\boldsymbol{\phi}}}\sin\phi\right) \left(\dfrac{\partial f}{\partial\rho}\dfrac{\partial\rho}{\partial x}+\dfrac{\partial f}{\partial\phi}\dfrac{\partial\phi}{\partial x} +\dfrac{\partial f}{\partial z}\dfrac{\partial z}{\partial x}\right)+ \\ + &\left(\mathbf{\hat{\boldsymbol{\rho}}}\sin\phi+\mathbf{\hat{\boldsymbol{\phi}}}\cos\phi\right) \left(\dfrac{\partial f}{\partial\rho}\dfrac{\partial\rho}{\partial y}+\dfrac{\partial f}{\partial\phi}\dfrac{\partial\phi}{\partial y} +\dfrac{\partial f}{\partial z}\dfrac{\partial z}{\partial y}\right)+\mathbf{\hat{z}}\dfrac{\partial f}{\partial z}. \end{aligned} $$

A.38

Jednotlivé parciální derivace vypočítáme z rovnice A.29,

$$ \begin{aligned} &\dfrac{\partial\rho}{\partial x}=\dfrac{x}{\sqrt{x^2+y^2}}=\cos\phi,\,\, \dfrac{\partial\phi}{\partial x}=-\dfrac{y}{x^2+y^2}=-\dfrac{\sin\phi}{\rho},\\ &\dfrac{\partial\rho}{\partial y}=\dfrac{y}{\sqrt{x^2+y^2}}=\sin\phi,\,\, \dfrac{\partial\phi}{\partial y}=\dfrac{x}{x^2+y^2}=\dfrac{\cos\phi}{\rho}. \end{aligned} $$

A.39

Po dosazení a úpravě dostaneme výslednou podobu gradientu

$$ \vec{\nabla}f=\mathbf{\hat{\boldsymbol{\rho}}}\dfrac{\partial f}{\partial\rho}+ \mathbf{\hat{\boldsymbol{\phi}}}\dfrac{1}{\rho}\dfrac{\partial f}{\partial\phi}+\mathbf{\hat{z}}\dfrac{\partial f}{\partial z}= \left(\dfrac{\partial f}{\partial\rho},\,\dfrac{1}{\rho}\dfrac{\partial f}{\partial\phi},\,\dfrac{\partial f}{\partial z}\right). $$

A.40

Nyní již za jednotkové vektory válcové báze nedosazujeme jejich složky z rovnice A.30, kde jsme je viděli ze soustavy kartézské. Analogicky k rovnici A.6 (tenzorový součin) a s použitím rovnice A.40 je potom gradient vektorového pole $\vec{A}\,(\rho,\,\phi,\,z)$ ve válcové soustavě definován jako tenzor 2. řádu ve tvaru

$$ \vec{\nabla}\vec{A}=\left(\mathbf{\hat{\boldsymbol{\rho}}}\dfrac{\partial}{\partial\rho}+ \mathbf{\hat{\boldsymbol{\phi}}}\dfrac{1}{\rho}\dfrac{\partial}{\partial\phi}+\mathbf{\hat{z}}\dfrac{\partial}{\partial z}\right) \left(A_\rho\mathbf{\hat{\boldsymbol{\rho}}}+A_{\phi}\mathbf{\hat{\boldsymbol{\phi}}}+A_z\mathbf{\hat{z}}\right). $$

A.41

Na rozdíl od kartézské soustavy zde již jednotkové bázové vektory $\mathbf{\hat{\boldsymbol{\rho}}}$ a $\mathbf{\hat{\boldsymbol{\phi}}}$ nejsou konstantní, operátor gradientu tedy fakticky působí i na ně (jejich derivace – viz rovnice A.31). Pomocí maticového formalismu můžeme tenzor gradientu vektorového pole ve válcové soustavě zapsat

A.42
Stejného výsledku docílíme v tomto případě i jiným postupem, např. s použitím formalismu Christoffelových symbolů (viz rovnice A.37), kde, na rozdíl od rovnice A.19, zapíšeme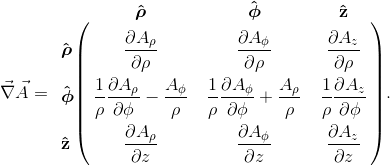

$$ \vec\nabla\vec{A}=\dfrac{1}{h_jh_k}\left[\nabla_j(h_kA_k)\right]\mathbf{\hat{x}}_j\mathbf{\hat{x}}_k= \dfrac{1}{h_jh_k}\left[\dfrac{\partial}{\partial x_j}(h_kA_k)-\Gamma_{jk}^lh_lA_l\right]\mathbf{\hat{x}}_j\mathbf{\hat{x}}_k. $$

A.43

Postup podle rovnice A.43 lze ovšem použít pouze pro ortogonální souřadné soustavy, postup podle rovnice A.41 platí zcela obecně.
Divergence vektoru (vektorového pole) $\vec{A}\,(\rho,\,\phi,\,z)$ je ve válcových souřadnicích ve smyslu rovnice A.41, analogicky k rovnici A.8, definována jako skalár (skalární pole)

$$ \begin{aligned} \vec{\nabla}\cdot\vec{A}=\mathbf{\hat{\boldsymbol{\rho}}}\cdot\mathbf{\hat{\boldsymbol{\rho}}}\, \dfrac{\partial A_\rho}{\partial\rho}+ \mathbf{\hat{\boldsymbol{\phi}}}\cdot\mathbf{\hat{\boldsymbol{\phi}}}\left(\dfrac{A_\rho}{\rho}+ \dfrac{1}{\rho}\dfrac{\partial A_{\phi}}{\partial\phi}\right)+ \mathbf{\hat{z}}\cdot\mathbf{\hat{z}}\,\dfrac{\partial A_z}{\partial z}=\\ =\dfrac{1}{\rho}\dfrac{\partial}{\partial\rho}\left(\rho A_\rho\right)+\dfrac{1}{\rho}\dfrac{\partial A_{\phi}}{\partial\phi}+ \dfrac{\partial A_z}{\partial z}. \end{aligned} $$

A.44

Porovnáním s rovnicí A.42 opět vidíme, že divergence je stopou tenzoru gradientu vektorového pole. Divergencí tenzoru 2. řádu, popsaného maticí $3\times 3$, bude vektor (tenzor 1. řádu). Explicitní formu zápisu divergence tenzoru 2. řádu ve válcových souřadnicích (srovnej s rovnicí A.17 zde již uvádět nebudu, zájemce odkazuji na literaturu, např. Abramowitz & Stegun (1972); Young (1993); Arfken & Weber (2005), atd.
Rotaci vektoru (vektorového pole) $\vec{A}\,(\rho,\,\phi,\,z)$ ve válcové soustavě, kde $h_\rho=1,\,h_{\phi}=\rho,\,h_z=1$, odvodíme podle již uvedeného vztahu A.20. Dostáváme

$$ \vec\nabla\times\vec{A}= \left(\dfrac{1}{\rho}\dfrac{\partial A_z}{\partial\phi}-\dfrac{\partial A_{\phi}}{\partial z}\right)\mathbf{\hat{\boldsymbol{\rho}}}+ \left(\dfrac{\partial A_\rho}{\partial z}-\dfrac{\partial A_z}{\partial\rho}\right)\mathbf{\hat{\boldsymbol{\phi}}}+ \dfrac{1}{\rho}\left[\dfrac{\partial}{\partial\rho}\left(\rho A_{\phi}\right)-\dfrac{\partial A_\rho}{\partial\phi}\right]\mathbf{\hat{z}}. $$

A.45
Laplacián odvodíme (viz rovnice A.22), nahradíme-li v rovnici divergence A.44 složky vektoru $\vec{A}$ odpovídajícími složkami vektoru gradientu z rovnice A.40. Dostáváme

$$ \begin{aligned} \Delta=\vec{\nabla}\cdot\vec{\nabla}= \mathbf{\hat{\boldsymbol{\rho}}}\cdot\dfrac{1}{\rho}\dfrac{\partial}{\partial\rho} \left(\rho\,\mathbf{\hat{\boldsymbol{\rho}}}\dfrac{\partial}{\partial\rho}\right)+ \mathbf{\hat{\boldsymbol{\phi}}}\cdot\dfrac{1}{\rho}\dfrac{\partial}{\partial\phi} \left(\mathbf{\hat{\boldsymbol{\phi}}}\dfrac{1}{\rho}\dfrac{\partial}{\partial\phi}\right)+ \mathbf{\hat{z}}\cdot\dfrac{\partial}{\partial z}\left(\mathbf{\hat{z}}\dfrac{\partial}{\partial z}\right)=\\ =\dfrac{1}{\rho}\dfrac{\partial}{\partial\rho}\left(\rho\dfrac{\partial}{\partial\rho}\right)+ \dfrac{1}{\rho^2}\dfrac{\partial^2}{\partial\phi^2}+\dfrac{\partial^2}{\partial z^2}.\end{aligned} $$

A.46

nahoru

A.2.2 Plochy, objemy

Stejně jako v kartézské soustavě označme $S_k$ plochu s konstantní hodnotou souřadnice $x_k$, ohraničenou souřadnicovými křivkami $x_i,x_i+\Delta x_i,x_j,x_j+\Delta x_j$. Ve válcové soustavě půjde např. o plochu s konstantní hodnotou $z=z_0$, ohraničenou polopřímkami $\phi=\phi_1,\phi=\phi_2$ a křivkami (kružnicemi) $\rho=\rho_1,\rho=\rho_2$. Výpočet velikosti takové plochy již není tak zcela triviální, jako v kartézské soustavě, půjde o průnik kruhové výseče s plochou mezi dvěma soustřednými kružnicemi. Pokud budeme uvažovat jinou plochu, např. s konstantní souřadnicí $\rho=\rho_0$, ohraničenou souřadnicovými plochami $\phi=\phi_1,\phi=\phi_2,z=z_1,z=z_2$, půjde o část válcové plochy. Při výpočtech velikostí těchto ploch vyjdeme z rovnic A.23 a A.36, tedy,

$$ \begin{aligned} S_\rho&=\int\limits_{\phi_1}^{\phi_2}\int\limits_{z_1}^{z_2}\sqrt{g_{\phi\phi}\,g_{zz}}\,\,\text{d} \phi\,\text{d} z= \int\limits_{\phi_1}^{\phi_2}\int\limits_{z_1}^{z_2}\rho\,\,\text{d}\phi\,\text{d} z=\rho\Delta\phi\Delta z,\\ S_\phi&=\int\limits_{z_1}^{z_2}\int\limits_{\rho_1}^{\rho_2}\sqrt{g_{zz}\,g_{\rho\rho}}\,\,\text{d} z\,\text{d}\rho= \int\limits_{z_1}^{z_2}\int\limits_{\rho_1}^{\rho_2}\,\text{d} z\,\text{d}\rho=\Delta z\Delta\rho,\\ S_z&=\int\limits_{\rho_1}^{\rho_2}\int\limits_{\phi_1}^{\phi_2}\sqrt{g_{\rho\rho}\,g_{\phi\phi}}\,\,\text{d}\rho\,\text{d}\phi= \int\limits_{\rho_1}^{\rho_2}\int\limits_{\phi_1}^{\phi_2}\rho\,\text{d}\rho\,\text{d}\phi=\dfrac{\rho_2^2-\rho_1^2}{2}\Delta\phi. \end{aligned} $$

A.47

Ve válcovém souřadném systému budou nediagonální členy submatic $J^\prime_{ij}$ (viz rovnice A.23) nulové. Označíme-li $V$ objem prostoru, vymezeného souřadnicovými plochami s konstantními souřadnicemi $\rho_1,\rho_2,\phi_1,\phi_2,z_1,z_2$, výpočet velikosti tohoto objemu bude mít dle rovnice A.24 tvar

$$ V=\int\limits_{\rho_1}^{\rho_2}\int\limits_{\phi_1}^{\phi_2}\int\limits_{z_1}^{z_2} \rho\,\text{d}\rho\,\text{d}\phi\,\text{d} z=\dfrac{\rho_2^2-\rho_1^2}{2}\Delta\phi\Delta z. $$

A.48

V ortogonálním válcovém souřadném systému můžeme Jakobián $J$ stanovit jako ${\sqrt{g_{\rho\rho}\,g_{\phi\phi}\,g_{zz}}}=\rho$. Obdobným způsobem můžeme při odpovídajícím stanovení integračních mezí vypočítat v daném souřadném systému velikost jakéhokoli jiného, složitějšího útvaru.

nahoru

A.2.3 Vektory polohy, rychlosti a zrychlení

Při popisu vektorů ve válcové soustavě vyjdeme z jejich popisu v soustavě kartézské, zahrneme všechny rovnice pro derivace jednotkových vektorů i vektorových složek (rovnice A.28-A.33). Polohový vektor a vektor rychlosti ve válcové soustavě budou

$$ \begin{aligned} \vec{r} &=x\mathbf{\hat{x}}+y\mathbf{\hat{y}}+z\mathbf{\hat{z}}=\rho\mathbf{\hat{\boldsymbol{\rho}}}+z\mathbf{\hat{z}},\\ \vec{v} &=\dfrac{\text{d}\vec{r}}{\text{d} t}=\dfrac{\text{d}\left(\rho\mathbf{\hat{\boldsymbol{\rho}}}+z\mathbf{\hat{z}}\right)}{\text{d} t}= \dot{\rho}\mathbf{\hat{\boldsymbol{\rho}}}+{\rho}\dot{\mathbf{\hat{\boldsymbol{\rho}}}}+\dot{z}\mathbf{\hat{z}}= \dot{\rho}\mathbf{\hat{\boldsymbol{\rho}}}+{\rho}\dot{\phi}\mathbf{\hat{\boldsymbol{\phi}}}+\dot{z}\mathbf{\hat{z}}. \end{aligned} $$

A.49

Tento tvar lze očekávat, uvědomíme-li si, že polohový vektor vždy vychází z počátku souřadnic. Vektory rychlosti a zrychlení jsou zároveň definovány jako

$$ \vec{v}=v_\rho\mathbf{\hat{\boldsymbol{\rho}}}+ v_\phi\mathbf{\hat{\boldsymbol{\phi}}}+v_z\mathbf{\hat{z}},\quad \vec{a}=\dfrac{\text{d}\vec{v}}{\text{d} t}=a_\rho\mathbf{\hat{\boldsymbol{\rho}}}+a_\phi\mathbf{\hat{\boldsymbol{\phi}}}+a_z\mathbf{\hat{z}}. $$

A.50

Derivováním rovnice A.49 podle času dostáváme jednotlivé složky vektoru zrychlení

$$ a_\rho=\ddot{\rho}-\rho\dot{\phi}^2 =\dfrac{\text{d} v_\rho}{\text{d} t}-\rho\dot{\phi}^2,\quad a_\phi=\rho\ddot{\phi}+2\dot{\rho}\dot{\phi} =\dfrac{\text{d} v_\phi}{\text{d} t}+\dot{\rho}\dot{\phi},\quad a_z=\ddot{z} =\dfrac{\text{d} v_z}{\text{d} t}. $$

A.51

Protože $\text{d}/\text{d} t=\partial/\partial t+\vec{v}\cdot\vec{\nabla}$ (řetězové pravidlo pro derivování, v tomto případě pro parciální derivace $\vec{v}=\vec{v}(t,\rho,\phi,z)$), potom zrychlení, vyjádřené pomocí složek vektoru rychlosti bude

$$ a_\rho =\frac{\partial v_\rho}{\partial t}+\underbrace{v_\rho\frac{\partial v_\rho}{\partial\rho}+ \frac{v_\phi}{\rho}\frac{\partial v_\rho}{\partial\phi} +v_z\frac{\partial v_\rho}{\partial z}}_{\left(\vec{v}\cdot\vec{\nabla}\right)v_\rho}-\frac{v_\phi^2}{\rho}, $$

A.52

$$ a_\phi =\frac{\partial v_\phi}{\partial t}+\underbrace{v_\rho\frac{\partial v_\phi}{\partial\rho}+ \frac{v_\phi}{\rho}\frac{\partial v_\phi}{\partial\phi} +v_z\frac{\partial v_\phi}{\partial z}}_{\left(\vec{v}\cdot\vec{\nabla}\right)v_\phi}+\frac{v_\rho v_\phi}{\rho}, $$

A.53

$$ a_z =\frac{\partial v_z}{\partial t}+\underbrace{v_\rho\frac{\partial v_z}{\partial\rho}+ \frac{v_\phi}{\rho}\frac{\partial v_z}{\partial\phi} +v_z\frac{\partial v_z}{\partial z}}_{\left(\vec{v}\cdot\vec{\nabla}\right)v_z}. $$

A.54