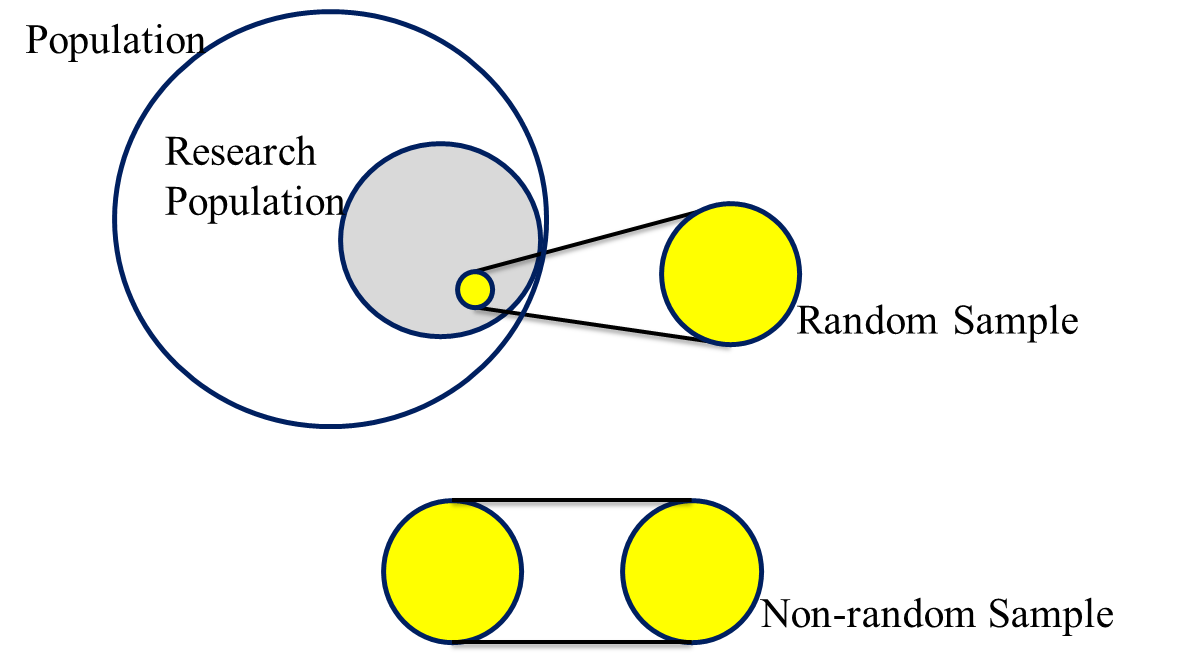
Sampling is a fundamental concept in research methodology, essential for conducting studies on populations that are too large to be studied in their entirety due to practical limitations such as cost, time, and other factors (Singh, 2006). In scientific research, we often study only a fragment of the phenomena to advance our knowledge. In this context, the fragment refers to the sample, and the phenomena represent the population.
Sampling is the process of selecting a subset (a sample) from a larger group (the sampling population) to estimate or predict unknown information, situations, or outcomes regarding the larger group (Kumar, 2011).
1.8.1 Method of Sampling
Sampling methods can be broadly categorised into probability sampling and non-probability sampling.
Random sampling (or probability sampling). In probability sampling, every element in the population has a known, non-zero chance of being included in the sample. This approach ensures that the sample is representative of the population, which is crucial for generalising findings.
Types of Random Sampling:
-
Simple Random Sampling: Each member of the population has an equal chance of being selected. This method is suitable for small, homogeneous populations. Example: a lottery system.
-
Systematic Random Sampling: Members of the population are selected according to a specific order or scheme. For instance, every 10th person on a list.
-
Stratified Random Sampling: The population is divided into distinct categories called “strata,” and random samples are selected from each stratum. Each stratum is proportionately filled to ensure representation.
-
Cluster Sampling: The population is divided into homogeneous units, often based on geographical contiguity. Units are selected as groups rather than individuals. Example: selecting schools within a city.
-
Multistage Sampling: A complex form of cluster sampling involving multiple levels of units embedded within each other. For example, selecting districts, then schools within districts, and then students within schools.
Non-random sampling (or non-probability sampling). In non-probability sampling, elements are selected based on availability, volunteering, or the researcher's judgment. This method does not provide a representative sample of the population, limiting the ability to generalise findings.
Types of Non-Random Sampling:
-
Convenience Sampling: Also known as grab, opportunity, accidental, or haphazard sampling. The sample is selected based on ease of access. This method does not allow for generalisations about the total population as it is not representative.
-
Purposive Sampling: The sample is selected based on the researcher's knowledge that it is representative of the total population. This method is used when specific characteristics are required.
-
Quota Sampling: Similar to stratified sampling, the population is divided into mutually exclusive sub-groups. However, selections are made in a non-random manner to fill specified proportions of the sample.
A good sample in sports research should exhibit the following qualities (Singh, 2006):
-
True Representation: The sample must accurately reflect the target population.
Example: If researchers are studying the effect of a new training regimen on elite football players, the sample should include players from a similar competitive level, age range, and physical conditioning to ensure the findings are generalisable to all elite football players.
-
Free from Bias: The selection process should avoid favouring any particular group.
Example: If a coach handpicks only the most motivated athletes for a training study, this could bias the results. Instead, random selection should be used to ensure all players have an equal chance of being included.
-
Objectivity: The criteria for selecting participants should be clear and not influenced by subjective factors.
Example: Athletes should be selected based on predefined fitness levels or training history, not personal preferences of the coach or researcher.
-
Comprehensive Nature: The sample should cover all relevant characteristics of the population.
Example: In a study examining injury prevention strategies, the sample should include athletes of different positions, injury histories, and training volumes to ensure a comprehensive view of the population.
-
Accuracy: The sampling method must ensure precise representation of the population.
Example: If studying performance trends in youth athletes, the sample should accurately reflect the age distribution of youth athletes across different sports and levels of participation.
-
Yield Accurate Results: The sample should lead to reliable and valid conclusions.
Example: If testing the effects of hydration strategies in endurance runners, the sample should include runners from various distances (e.g., marathon, ultramarathon) to ensure the results apply broadly across endurance disciplines.
Sample Size
A general rule in research is that a larger sample size is better, as it is likely more representative of the population and yields data that are more accurate and precise with smaller standard errors. However, this is not always true. Increasing the sample size can also increase the chances of a Type I Error (false positive), where the researcher incorrectly claims a significant effect when there is none. This risk can be mitigated by using effect size tests (Chapter 2.9 The Effect Size), which measure the magnitude of the effect and provide more meaningful interpretations of the results.
Statistical Power
Statistical power is the probability that a test correctly rejects the null hypothesis when it is false, thus detecting an effect when there is one. Higher statistical power reduces the probability of a Type II Error (false negative), where the researcher fails to detect a significant effect that actually exists.
Key Points about Statistical Power:
Selecting suitable statistical tests for your data set is crucial, as some tests are more reliable with larger sample sizes (n > 20), while others are designed for smaller samples.
Researchers can calculate the ideal sample size needed to achieve sufficient statistical power to correctly reject the null hypothesis. This can be done using statistical power calculators or sample size calculators (available online).
Review Questions
-
What are the main differences between probability and non-probability sampling methods?
-
Describe the process of stratified random sampling.
-
Why is convenience sampling not suitable for generalising findings to the entire population?
-
List the characteristics of a good sample.
-
Explain the concept of multistage sampling with an example.
-
What are the potential risks of using a larger sample size in research?
-
How can researchers determine the ideal sample size for their study?