Vztah – aritmetický průměr ∼ geometrický průměr

Dokažte, že platí: aritmetický průměr dvou nezáporných čísel je větší nebo roven jejich geometrickému průměru.

Důkaz 1.

algebraicky

$$\begin{aligned} \dfrac {a+b} 2 & \ge \sqrt{ab} \\ (a+b)^2 & \ge 4ab \\ a^2 + 2ab + b^2 & \ge 4ab \\ a^2 - 2ab + b^2 & \ge 0 \\ (a-b)^2 & \ge 0 \text { - platí vždy} \end{aligned} $$

geometricky

1. sestrojíme úsečku AC o velikosti $a+b$
2. sestrojíme kružnici $k$ o poloměru $\dfrac {a+b} 2$
3. v bodě B narýsujeme kolmici k úsečce AC
4. v trojúhelníku ACD je úsečka BD výškou ke straně AC
5. podle Euklidovy věty $v=\sqrt{ab}$

$$ \begin{aligned} d & =a+b \\ r & = \frac{(a+b)} 2 \\ \frac {a+b} 2 & \ge \sqrt{ab} \end{aligned} $$

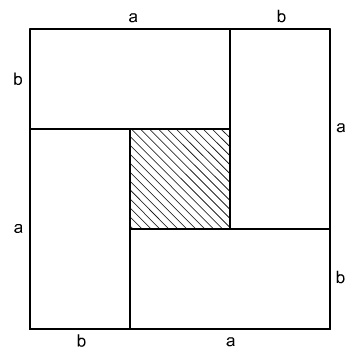
Jiný důkaz věty o vztahu aritmetického a geometrického průměru

geometricky

$$ \begin{aligned} (a+b)^2 & \ge 4ab \\ a+b & \ge 2\sqrt {ab} \\ \frac {a+b} 2 & \ge \sqrt {ab} \end{aligned} $$