Přechod na menu, Přechod na obsah, Přechod na patičku
     

II. 5. Aplikace integrálního počtu



nahoru

Geometrické aplikace



  • Určitý integrál

    S=\displaystyle\int\limits_a^b \left|f(x)\right|\,\mathrm{d}x

    lze geometricky interpretovat jako obsah plochy vymezené grafem funkce f v intervalu [a,b].
  • Obsah obrazce ohraničeného uzavřenou křivkou o parametrických souřadnicích x=\varphi(t) a y=\psi(t) pro t\in[\alpha,\beta]:

    S=-\displaystyle\int\limits_{\alpha}^{\beta}\psi(t)\,\varphi'(t)\,\mathrm{d}t=\displaystyle\int\limits_{\alpha}^{\beta}\varphi(t)\,\psi'(t)\,\mathrm{d}t=\\ \phantom{S} =\dfrac{1}{2}\displaystyle\int\limits_{\alpha}^{\beta}\left[\varphi(t)\,\psi'(t)-\psi(t)\,\varphi'(t)\right]\mathrm{d}t.

    Křivka je orientována kladně, tzn., že plocha leží nalevo od křivky.
  • Obsah plochy vymezené grafy funkcí f a g v intervalu [a,b] vypočteme pomocí určitého integrálu

    S=\displaystyle\int\limits_a^b \left|f(x)-g(x)\right|\,\mathrm{d}x.

  • Délka grafu funkce f pro x\in[a,b]:

    l=\displaystyle\int\limits_a^b\sqrt{1+[f'(x)]^2}\,\mathrm{d}x.

  • Délka křivky zadané parametricky x=\varphi(t) a y=\psi(t) pro t\in[\alpha,\beta]:

    l=\displaystyle\int\limits_{\alpha}^{\beta}\sqrt{[\varphi'(t)]^2+[\psi'(t)]^2}\,\mathrm{d}t.

  • Objem rotačního tělesa, které vznikne rotací podgrafu spojité nezáporné funkce f, x\in[a,b] kolem osy  x:

    V_x=\pi\displaystyle\int\limits_a^b f^2(x)\,\mathrm{d}x.

  • Objem rotačního tělesa, které vznikne rotací podgrafu spojité nezáporné funkce f, x\in[a,b], a > 0, kolem osy  y:

    V_y=2\pi\displaystyle\int\limits_a^b xf(x)\,\mathrm{d}x.

  • Objem rotačního tělesa, které vznikne rotací plochy vymezené křivkou zadanou parametricky x=\varphi(t) a y=\psi(t) pro t\in[\alpha,\beta], \psi(t) \ge 0, kolem osy x:

    V_x=\pi\displaystyle\int\limits_{\alpha}^{\beta} \psi^2(t)\cdot\left|\varphi'(t)\right|\,\mathrm{d}t.

  • Objem rotačního tělesa, které vznikne rotací plochy vymezené křivkou zadanou parametricky x=\varphi(t) a y=\psi(t) pro t\in[\alpha,\beta], \psi(t) \ge 0, kolem osy y:

    V_y=2\pi\displaystyle\int\limits_{\alpha}^{\beta} \psi(t)\,\varphi(t)\left|\,\varphi'(t)\right|\,\mathrm{d}t.

  • Obsah pláště rotačního tělesa, které vznikne rotací spojitě diferencovatelné nezáporné podgrafu funkce f(x), x\in[a,b] kolem osy x

    Q_x=2\pi\displaystyle\int\limits_a^b f(x)\sqrt{1+[f'(x)]^2}\,\mathrm{d}x.

  • Obsah pláště rotačního tělesa , které vznikne rotací plochy vymezené křivkou zadanou parametricky x=\varphi(t) a y=\psi(t) pro t\in[\alpha,\beta], \psi (t) \ge 0, kolem osy x

    Q_x=2\pi\displaystyle\int\limits_{\alpha}^{\beta} \psi(t)\sqrt{[\varphi'(t)]^2+[\psi'(t)]^2}\,\mathrm{d}t.

nahoru

Fyzikální aplikace



Funkce s(t) udává délkovou hustotu v bodě [\varphi(t),\psi(t)] pro křivku zadanou parametricky x=\varphi(t) a  y=\psi(t), t\in[\alpha,\beta]. Potom M vyjadřuje hmotnost křivky a

\left[\dfrac{S_y}{M},\dfrac{S_x}{M}\right]

jsou souřadnice jejího těžiště, kde S_x a S_y jsou tzv. statické momenty křivky vzhledem k ose x, resp. y, přičemž platí

M =\displaystyle\int\limits_{\alpha}^{\beta}s(t)\sqrt{[\varphi'(t)]^2+[\psi'(t)]^2}\,\mathrm{d}t,
S_x =\displaystyle\int\limits_{\alpha}^{\beta}s(t)\psi(t)\sqrt{[\varphi'(t)]^2+[\psi'(t)]^2}\,\mathrm{d}t,
S_y =\displaystyle\int\limits_{\alpha}^{\beta}s(t)\varphi(t)\sqrt{[\varphi'(t)]^2+[\psi'(t)]^2}\,\mathrm{d}t.

Nechť nyní funkce s(x) udává délkovou hustotu v bodě [x,f(x)] pro křivku grafem funkce f, x\in[a,b]. Potom platí

M =\displaystyle\int\limits_a^b s(x)\sqrt{1+[f'(x)]^2}\,\mathrm{d}x,
S_x =\displaystyle\int\limits_a^b s(x)f(x)\sqrt{1+[f'(x)]^2}\,\mathrm{d}x,
S_y =\displaystyle\int\limits_a^b xs(x)\sqrt{1+[f'(x)]^2}\,\mathrm{d}x.

Funkce S(t) udává hustotu obrazce vymezeného křivkou zadanou parametricky x=\varphi(t) a  y=\psi(t), t\in[\alpha,\beta]. Potom M vyjadřuje jeho hmotnost a

\left[\dfrac{S_y}{M},\dfrac{S_x}{M}\right]

jsou souřadnice jeho těžiště, přičemž platí

M =\displaystyle\int\limits_{\alpha}^{\beta}S(t)\psi(t)\varphi'(t)\,\mathrm{d}t,
S_x =\dfrac{1}{2}\displaystyle\int\limits_{\alpha}^{\beta}S(t)\psi^2(t)\varphi'(t)\,\mathrm{d}t,
S_y =\displaystyle\int\limits_{\alpha}^{\beta}S(t)\psi(t)\varphi(t)\varphi'(t)\,\mathrm{d}t.

Nechť nyní funkce S(t) udává hustotu obrazce vymezeného křivkou určenou grafem nezáporné spojité funkce f, x\in[a,b], a osou x. Potom M vyjadřuje jeho hmotnost a

\left[\dfrac{S_y}{M},\dfrac{S_x}{M}\right]

jsou souřadnice jeho těžiště, přičemž platí

M =\displaystyle\int\limits_a^b S(x)f(x)\,\mathrm{d}x,
S_x =\dfrac{1}{2}\displaystyle\int\limits_a^b S(x)f^2(x)\,\mathrm{d}x,
S_y =\displaystyle\int\limits_a^b xS(x)f(x)\,\mathrm{d}x.
Příklad č. 436» Zobrazit zadání «

Určete obsah plochy vymezené grafy funkcí f(x)=x^2+x-3 a g(x)=-x^2-2x+2.

Řešení» Zobrazit řešení «

Nejdříve musíme určit průsečík obou funkcí, tj. vyřešit rovnici f(x)=g(x), tzn. že

2x^2+3x-5=0\quad \Rightarrow\quad x_{1}=-\dfrac{5}{2}\text{ a }x_{2}=1.

Graf

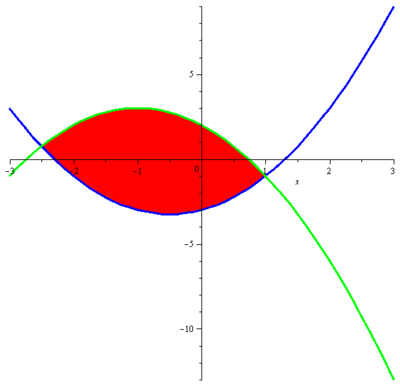
Navíc, v intervalu [-\frac{5}{2},1] platí g(x)>f(x), proto hledaný obsah vypočteme s pomocí následujícího integrálu

S =\displaystyle\int\limits_{-\frac{5}{2}}^{1}\left[(-x^2-2x+2)-(x^2+x-3)\right]\,\mathrm{d} x=\displaystyle\int\limits_{-\frac{5}{2}}^{1}\left(-2x^2-3x+5\right)\,\mathrm{d} x=
= \left[-\dfrac{2x^3}{3}-\dfrac{3x^2}{2}+5x\right]_{-\frac{5}{2}}^{1}= -\dfrac{2}{3}-\dfrac{3}{2}+5-\left(\dfrac{250}{54}-\dfrac{75}{8}-\dfrac{25}{2}\right)=\dfrac{343}{24}.
Příklad č. 437» Zobrazit zadání «

Určete obsah plochy ohraničené křivkami x^2+y^2=2 a y=x^2.

Řešení» Zobrazit řešení «

Nejdříve musíme určit průsečík obou funkcí, tj.

y+y^2=2\quad \Rightarrow\quad y_{1}=-2\text{ a }y_{2}=1.

Graf

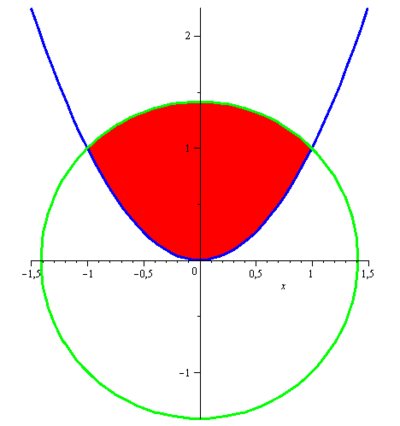
Vzhledem k podmínce y=x^2 je pro nás zajímavá pouze hodnota y_{2}. Potom x_{1}=-1 a x_{2}=1. Navíc, na intervalu [-1,1] platí \sqrt{2-x^2}>x^2, proto hledaný obsah dostaneme pomocí integrálu

S =\displaystyle\int\limits_{-1}^{1}\left(\sqrt{2-x^2}-x^2\right)\mathrm{d} x=2\left[\dfrac{x}{2}\sqrt{2-x^2}+\operatorname{arcsin}\left(\dfrac{x}{\sqrt{2}}\right)-\dfrac{x^3}{3}\right]_{0}^{1}=
= 2\left(\dfrac{1}{2}+\operatorname{arcsin}\dfrac{1}{\sqrt{2}}-\dfrac{1}{3}-0\right)=\dfrac{1}{3}+\dfrac{\pi}{2}.

Při výpočtu jsme využili následující integrál

\displaystyle\int\sqrt{2-x^2}\,\mathrm{d} x \left\bracevert\begin{matrix} \dfrac{x}{\sqrt{2}}=\sin t\\ \dfrac{\mathrm{d} x}{\sqrt{2}}=\cos t\,\mathrm{d} t \end{matrix}\right\bracevert =\displaystyle\int\sqrt{2-2\sin^2 t}\,\sqrt{2}\cos t\,\mathrm{d} t=
\hspace*{5mm}= \sqrt{2}\displaystyle\int\sqrt{1-\sin^{2}t}\,\sqrt{2}\cos t\,\mathrm{d} t=
\hspace*{5mm}=2\displaystyle\int\cos^2t\,\mathrm{d} t \left\bracevert\begin{matrix} \cos 2t=2\cos^{2}t-1 \end{matrix}\right\bracevert =
\hspace*{5mm}= 2\displaystyle\int\left(\dfrac{1}{2}\cos 2t+\dfrac{1}{2}\right)\mathrm{d} t= \displaystyle\int\left(\cos 2t+1\right)\mathrm{d} t=\dfrac{1}{2}\sin 2t+t+C=
\hspace*{5mm}= \sin t\cos t+\operatorname{arcsin}\left(\dfrac{x}{\sqrt{2}}\right)+C= \dfrac{x}{\sqrt{2}}\sqrt{1-\dfrac{x^2}{2}}+\operatorname{arcsin}\left(\dfrac{x}{\sqrt{2}}\right)+C=
\hspace*{5mm}= \dfrac{x}{2}\sqrt{2-x^2}+\operatorname{arcsin}\left(\dfrac{x}{\sqrt{2}}\right)+C.
Příklad č. 438» Zobrazit zadání «

Určete obsah oblouku cykloidy x=t-\sin t, y=1-\cos t, t\in[0,2\pi].

Řešení» Zobrazit řešení «

Graf

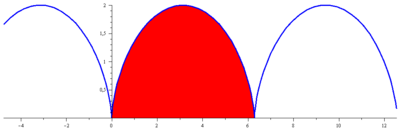
Dosazením do vzorce pro obsah plochy mezi parametricky zadanými křivkami obdržíme

S =\displaystyle\int\limits_{0}^{2\pi}\left(1-\cos t\right)\left(1-\cos t\right)\mathrm{d} t=
=\displaystyle\int\limits_{0}^{2\pi}\left(1-2\cos t+\cos^2t\right)\mathrm{d} t \left\bracevert\begin{matrix} \cos^2t=\dfrac{1}{2}+\dfrac{1}{2}\cos2t \end{matrix}\right\bracevert =
= \displaystyle\int\limits_{0}^{2\pi}\left(\dfrac{3}{2}-2\cos t+\dfrac{1}{2}\cos2t\right)\mathrm{d} t= \left[\dfrac{3}{2}t-2\sin t+\dfrac{1}{4}\sin 2t\right]_{0}^{2\pi}=3\pi.
Příklad č. 439» Zobrazit zadání «

Určete, v jakém poměru dělí křivka P: y^2=2x plochu kruhu K: x^2+y^2=8.

Řešení» Zobrazit řešení «

Zadání je znázorněno na následujícím obrázku.

Graf

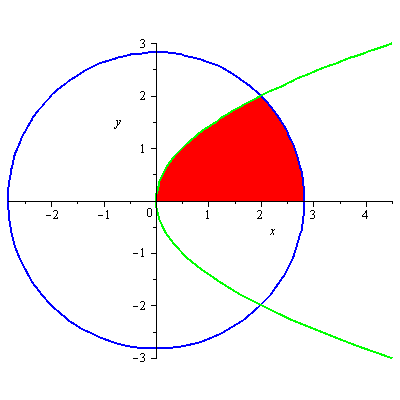
Z obrázku je zřejmé, že ve stejném poměru, jako dělí parabola kruh, dělí horní větev paraboly y=\sqrt{2x} horní půlkruh y=\sqrt{8-x^2}. Pro výpočet budeme potřebovat souřadnice průsečíku horní větve paraboly a horního půlkruhu. Poznamenejme, že nás zajímá pouze průsečík v I. kvadrantu, což nám umožní volnější úpravy.

\hspace{18,2mm} y=y,
\hspace{12,6mm}\sqrt{2x}=\sqrt{8-x^2},
\hspace{16,2mm}2x =8-x^2,
x^2+2x-8=0,
\hspace{18,2mm}x=2.

Průsečík má tedy souřadnice [2,2]. Nyní spočítáme obsah červeně vyznačené plochy.

S = \displaystyle\int\limits_0^2 \sqrt{2x} \,\mathrm{d} x + \displaystyle\int\limits_2^{\sqrt{8}} \sqrt{8-x^2} \,\mathrm{d} x = \dfrac{2\sqrt{2}}{3} \left[x^{\frac{3}{2}}\right]_0^2 + \displaystyle\int\limits_2^{\sqrt{8}} \sqrt{8-x^2} \,\mathrm{d} x =
= \dfrac{8}{3} + \displaystyle\int\limits_2^{\sqrt{8}} \sqrt{8-x^2} \,\mathrm{d} x \left\bracevert\begin{matrix} x=\sqrt{8}\sin t \vspace{2mm}\\ \mathrm{d} x = \sqrt{8}\cos t \,\mathrm{d} t \vspace{2mm}\\ \sqrt{8} \rightsquigarrow \dfrac{\pi}{2} =\vspace{2mm}\\ 2 \rightsquigarrow \dfrac{\pi}{4} \end{matrix}\right\bracevert =
= \dfrac{8}{3} + \displaystyle\int\limits_{\frac{\pi}{4}}^{\frac{\pi}{2}} \sqrt{8-8\sin^2 t} \sqrt{8} \cos t \,\mathrm{d} t =
= \dfrac{8}{3} + \displaystyle\int\limits_{\frac{\pi}{4}}^{\frac{\pi}{2}} 8 \cos^2 t \,\mathrm{d} t = \dfrac{8}{3} + 8 \displaystyle\int\limits_{\frac{\pi}{4}}^{\frac{\pi}{2}} \dfrac{1+\cos 2t}{2} \,\mathrm{d} t =
= \dfrac{8}{3} + 4 \displaystyle\int\limits_{\frac{\pi}{4}}^{\frac{\pi}{2}} 1+\cos 2t \,\mathrm{d} t = \dfrac{8}{3} + 4 \left[t+\dfrac{\sin2t}{2}\right]_{\frac{\pi}{4}}^{\frac{\pi}{2}} =
= \dfrac{8}{3} + 4 \left(\dfrac{\pi}{2} + 0 - \dfrac{\pi}{4} - \dfrac{1}{2}\right) = \dfrac{2}{3} + \pi.

Z rovnice kruhu vidíme, že jde o kruh o poloměru \sqrt{8}. Protože červená plocha má obsah
\frac{2}{3} + \pi , zbytek horního půlkruhu má obsah 4\pi - \left(\frac{2}{3} + \pi \right) = 3\pi - \frac{2}{3}. Hledaný poměr je tedy

\left(3\pi - \dfrac{2}{3}\right) : \left(\pi + \dfrac{2}{3}\right),

neboli

(9\pi-2) : (3\pi+2).

Příklad č. 440» Zobrazit zadání «

Odvoďte vzorec pro výpočet plochy elipsy s poloosami a a b.

Řešení» Zobrazit řešení «

Obecná rovnice zadané elipsy je tvaru

E: \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1.

Tato rovnice zadává implicitně funkci horní a dolní půlelipsy. Příklad vyřešíme tak, že si z rovnice elipsy explicitně vyjádříme funkci horní půlelipsy a pomocí ní pak spočítáme obsah čtvrtiny elipsy, která se nachází v I. kvadrantu.

Graf

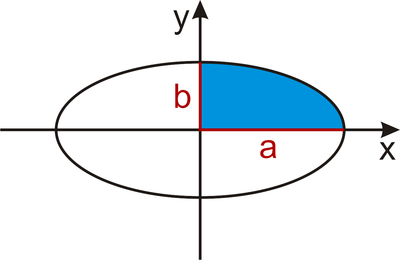
Horní půlelipsa je dána funkcí

f: y = b \sqrt{1-\dfrac{x^2}{a^2}}.

Interval, na kterém tato funkce zadává čtvrtelipsu v I. kvadrantu je x \in [0,a]. Můžeme tedy počítat

\dfrac{S}{4} = \displaystyle\int\limits_0^a b \sqrt{1-\dfrac{x^2}{a^2}} \,\mathrm{d} x = b \displaystyle\int\limits_0^a \sqrt{1-\dfrac{x^2}{a^2}} \,\mathrm{d} x \left\bracevert\begin{matrix} \dfrac{x}{a}=\sin t \\ \mathrm{d} x = a \cos t \,\mathrm{d} t \\ a \rightsquigarrow \dfrac{\pi}{2} \\ 0 \rightsquigarrow 0 \end{matrix}\right\bracevert =
= ab \displaystyle\int\limits_0^{\frac{\pi}{2}} \sqrt{1-\sin^2 t} \cos t \,\mathrm{d} t = ab \displaystyle\int\limits_0^{\frac{\pi}{2}} \cos^2 t \,\mathrm{d} t = \dfrac{ab}{2} \displaystyle\int\limits_0^{\frac{\pi}{2}} 1+\cos 2t \,\mathrm{d} t =
= \dfrac{ab}{2} \left[t+\dfrac{\sin 2t}{2}\right]_0^{\frac{\pi}{2}} = \dfrac{ab\pi}{4}.

Vzorec pro obsah elipsy s poloosami a a b je tedy

S = \pi ab.

Příklad č. 441» Zobrazit zadání «

Určete délku grafu funkce f(x)=\ln x pro x\in[\sqrt{3},\sqrt{15}].

Řešení» Zobrazit řešení «

Dosazením do vzorce dostaneme

l =\displaystyle\int\limits_{\sqrt{3}}^{\sqrt{15}}\sqrt{1+\dfrac{1}{x^2}}\,\mathrm{d} x=\displaystyle\int\limits_{\sqrt{3}}^{\sqrt{15}}\sqrt{\dfrac{1+x^2}{x^2}}\,\mathrm{d} x =
=\displaystyle\int\limits_{\sqrt{3}}^{\sqrt{15}}{\dfrac{\sqrt{1+x^2}}{x}}\,\mathrm{d} x \left\bracevert\begin{matrix} t^2=x^2+1\\ 2t\,\mathrm{d} t=2x\,\mathrm{d} x\\ \sqrt{3}\rightsquigarrow2\\ \sqrt{15}\rightsquigarrow4 \end{matrix}\right\bracevert =
= \displaystyle\int\limits_{2}^{4}\dfrac{\sqrt{t^2}}{t^2-1}\,t\,\mathrm{d} t= \displaystyle\int\limits_{2}^{4}\dfrac{t^2}{t^2-1}\,\mathrm{d} t=
= \displaystyle\int\limits_{2}^{4}\dfrac{t^2-1+1}{t^2-1}\,\mathrm{d} t= \displaystyle\int\limits_{2}^{4}\left(1+\dfrac{1}{t^2-1}\right)\,\mathrm{d} t=
= \displaystyle\int\limits_{2}^{4}\left(1+\dfrac{\frac{1}{2}}{t-1}-\dfrac{\frac{1}{2}}{t+1}\right)\,\mathrm{d} t= \left[t+\dfrac{1}{2}\ln \lvert t-1 \rvert -\dfrac{1}{2}\ln \lvert t+1 \rvert \right]_{2}^{4}=
= 4+\dfrac{1}{2}\ln3-\dfrac{1}{2}\ln5-2-\dfrac{1}{2}\ln1+\dfrac{1}{2}\ln3= 2+\ln3-\dfrac{1}{2}\ln5.
Příklad č. 442» Zobrazit zadání «

Určete délku oblouku cykloidy x=t-\sin t, y=1-\cos t, t\in[0,2\pi].

Řešení» Zobrazit řešení «

Aplikací odpovídajícího vzorce obdržíme

l =\displaystyle\int\limits_{0}^{2\pi}\sqrt{\left(\sin t\right)^2+\left(1-\cos t\right)^2}\,\mathrm{d} t= \displaystyle\int\limits_{0}^{2\pi}\sqrt{2-2\cos t}\,\mathrm{d} t \left\bracevert\begin{matrix} 1-\cos t=2\sin^2\dfrac{t}{2} \end{matrix}\right\bracevert =
= 2\displaystyle\int\limits_{0}^{2\pi}\sin\dfrac{t}{2}\,\mathrm{d} t= \left[-4\cos\dfrac{t}{2}\right]_{0}^{2\pi}=8.
Příklad č. 443» Zobrazit zadání «

Určete délku oblouku řetězovky f(x) = a \cosh \frac{x}{a}, I=[-1,1].

Řešení» Zobrazit řešení «

Připomeňme, že platí

\sinh x = \dfrac{\operatorname{e}^x-\operatorname{e}^{-x}}{2}, \qquad \cosh^2 x - \sinh^2 x = 1.

l =\displaystyle\int\limits_{-1}^{1}\sqrt{1+\sinh^2 \dfrac{x}{a}} \,\mathrm{d} x =\displaystyle\int\limits_{-1}^{1}\sqrt{\cosh^2 \dfrac{x}{a}} \,\mathrm{d} x \left\bracevert\begin{matrix} \cosh \text{ je všude kladný} \end{matrix}\right\bracevert =
= \displaystyle\int\limits_{-1}^{1} \cosh \dfrac{x}{a} \,\mathrm{d} x = \left[a \sinh\dfrac{x}{a}\right]_{-1}^1 = a \left(\sinh\dfrac{1}{a}-\sinh\dfrac{-1}{a}\right) =
= a (\operatorname{e}^{\frac{1}{a}}-\operatorname{e}^{-\frac{1}{a}}).
Příklad č. 444» Zobrazit zadání «

Vypočtěte délku oblouku křivky f(x)=\ln\frac{\operatorname{e}^x+1}{\operatorname{e}^x-1} pro x\in[1,2].

Řešení» Zobrazit řešení «

Nejdříve vypočteme a upravíme výrazy potřebné pro výpočet integrálu, tj.

f'(x)=\dfrac{-2\operatorname{e}^{x}}{\left(\operatorname{e}^{x}+1\right)\left(\operatorname{e}^{x}-1\right)}\quad \Rightarrow\quad \sqrt{1+\left[f'(x)\right]^{2}}=
=\sqrt{\dfrac{\operatorname{e}^{4x}+2\operatorname{e}^{2x}+1}{\left(\operatorname{e}^{x}+1\right)^2\left(\operatorname{e}^{x}-1\right)^2}}=\dfrac{1+\operatorname{e}^{2x}}{\operatorname{e}^{2x}-1}.

Proto můžeme spočítat

l =\displaystyle\int\limits_{2}^{1}\dfrac{1+\operatorname{e}^{2x}}{\operatorname{e}^{2x}-1}\,\mathrm{d} t=\displaystyle\int\limits_{2}^{1}\left(\dfrac{1}{\operatorname{e}^{2x}-1}+\dfrac{\operatorname{e}^{2x}}{{\operatorname{e}^{2x}-1}}\right)\mathrm{d} x=
=\left[-x+\dfrac{1}{2}\ln \lvert \operatorname{e}^{2x}-1 \rvert +\dfrac{1}{2}\ln \lvert \operatorname{e}^{2x}-1 \rvert \right]_{1}^{2}=
= \left(-2+\ln\left(\operatorname{e}^{4}-1\right)+1-\ln\left(\operatorname{e}^{2}-1\right)\right)= -1+\ln\dfrac{\left(\operatorname{e}^{2}-1\right)\left(\operatorname{e}^{2}+1\right)}{\operatorname{e}^{2}-1}=
=\ln\left(\operatorname{e}^{2}+1\right)-1=\ln\dfrac{\operatorname{e}^2+1}{\operatorname{e}},

přičemž jsme využili následující dva integrály

  1. \displaystyle\int\dfrac{\mathrm{d} x}{\operatorname{e}^{2x}-1} \left\bracevert\begin{matrix} t=2x\\ \mathrm{d} t=2\,\mathrm{d} x \end{matrix}\right\bracevert =\dfrac{1}{2}\displaystyle\int\dfrac{\mathrm{d} t}{\operatorname{e}^{t}-1}= \dfrac{1}{2}\displaystyle\int\dfrac{\operatorname{e}^{t}}{\operatorname{e}^{2t}-\operatorname{e}^{t}}\,\mathrm{d} t \left\bracevert\begin{matrix} \operatorname{e}^{t}=u\\ \operatorname{e}^{t}\,\mathrm{d} t=\mathrm{d} u \end{matrix}\right\bracevert =
    \hspace{5mm}= \dfrac{1}{2}\displaystyle\int\dfrac{\mathrm{d} u}{u^2-u}= \dfrac{1}{2}\displaystyle\int\left(-\dfrac{1}{u}+\dfrac{1}{1+u}\right)\mathrm{d} u=
    \hspace{5mm}= -\dfrac{1}{2}\ln \lvert u \rvert +\dfrac{1}{2}\ln \lvert u-1 \rvert +C=
    \hspace{5mm}= -\dfrac{1}{2}t+\dfrac{1}{2}\ln \lvert \operatorname{e}^{t}-1 \rvert +C= -x+\dfrac{1}{2}\ln \lvert \operatorname{e}^{2x}-1 \rvert +C;
  2. \displaystyle\int\dfrac{\operatorname{e}^{2x}}{\operatorname{e}^{2x}-1}\,\mathrm{d} x \left\bracevert\begin{matrix} t=\operatorname{e}^{2x}\\ \mathrm{d} t=2\operatorname{e}^{2x}\,\mathrm{d} x \end{matrix}\right\bracevert =\\ \hspace*{5mm} = \dfrac{1}{2}\displaystyle\int\dfrac{\mathrm{d} t}{t-1}= \dfrac{1}{2}\ln \lvert t-1 \rvert +C=\dfrac{1}{2}\ln \lvert \operatorname{e}^{2x}-1 \rvert +C.
Příklad č. 445» Zobrazit zadání «

Určete objem rotačního tělesa, které vznikne rotací podgrafu funkce f(x)=1+\frac{1}{2}\sin3x, x\in[\frac{\pi}{3},\frac{13\pi}{6}], kolem osy x.

Řešení» Zobrazit řešení «
V_x =\pi\displaystyle\int\limits_{\frac{\pi}{3}}^{\frac{13\pi}{6}}\left(1+\dfrac{1}{2}\sin3x\right)^2\mathrm{d} x=
= \pi\displaystyle\int\limits_{\frac{\pi}{3}}^{\frac{13\pi}{6}}\left(1+\sin3x+\dfrac{1}{4}\sin^2 3x\right)\mathrm{d} x \left\bracevert\begin{matrix} \sin^2 3x=\dfrac{1}{2}\left(1-\cos 6x\right) \end{matrix}\right\bracevert =
= \pi\displaystyle\int\limits_{\frac{\pi}{3}}^{\frac{13\pi}{6}}\left(1+\sin3x+\dfrac{1}{8}\left(1-\cos 6x\right)\right)\mathrm{d} x=
= \pi\left[x-\dfrac{1}{3}\cos 3x+\dfrac{1}{8}x-\dfrac{1}{48}\sin 6x\right]_{\frac{\pi}{3}}^{\frac{13\pi}{6}}= \dfrac{33\pi^2}{16}-\dfrac{\pi}{3}.
Příklad č. 446» Zobrazit zadání «

Vypočtěte objem tělesa, které vznikne rotací podgrafu funkce f(x)=\frac{1}{1+x^2}, x\in[-1,1], kolem osy x.

Řešení» Zobrazit řešení «

Graf

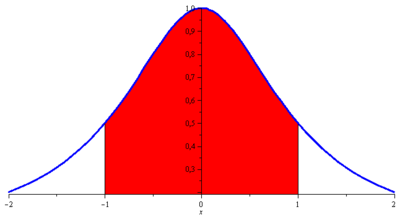
Poněvadž funkce f je sudá, můžeme spočítat poloviční objem na intervalu [0,1]. Proto

V_x=2\pi\displaystyle\int\limits_{0}^{1}\left(\dfrac{1}{1+x^2}\right)^2\mathrm{d} x=2\pi\left[\dfrac{1}{2}\operatorname{arctg} x+\dfrac{1}{2}\,\dfrac{x}{1+x^2}\right]_{0}^{1}=\\ \hspace*{3mm} = 2\pi\left(\dfrac{\pi}{8}+\dfrac{1}{4}\right)= \dfrac{\pi}{4}(\pi+2),

neboť

\displaystyle\int\left(\dfrac{1}{1+x^2}\right)^2\mathrm{d} x=K_{2}(0,1)=\dfrac{1}{2}K_{1}(0,1)+\dfrac{1}{2}\,\dfrac{x}{1+x^2}= \vspace{1mm}\\ \hspace*{28mm}=\dfrac{1}{2}\operatorname{arctg} x+\dfrac{1}{2}\,\dfrac{x}{1+x^2}+C.

Příklad č. 447» Zobrazit zadání «

Určete objem tělesa, které vznikne rotací prvního oblouku cykloidy x=t-\sin t, y=1-\cos t, t\in[0,2\pi], kolem osy x.

Řešení» Zobrazit řešení «
V =\pi\displaystyle\int\limits_{0}^{2\pi}\left(1-\cos t\right)^2\left(1-\cos t\right)\mathrm{d} t=\pi\displaystyle\int\limits_{0}^{2\pi}\left(1-\cos t\right)^3\mathrm{d} t=
= \pi\displaystyle\int\limits_{0}^{2\pi}\left(1-3\cos t+3\cos^2t-\cos^3 t\right)^3\mathrm{d} t=
= \pi\left[t-3\sin t+\dfrac{3}{2}t+\dfrac{3}{4}\sin 2t-\sin t+\dfrac{\sin^3 t}{3}\right]_{0}^{2\pi}=\pi\left(2\pi+3\pi\right)=5\pi^2,

neboť platí

  1. \displaystyle\int\cos^2t\,\mathrm{d} t =\displaystyle\int\dfrac{1+\cos 2t}{2}\,\mathrm{d} t=\dfrac{t}{2}+\dfrac{\sin 2t}{4}+C;
  2. \displaystyle\int\cos^3t\,\mathrm{d} t =\displaystyle\int\left(1-\sin^2 t\right) \cos t\,\mathrm{d} t \left\bracevert\begin{matrix} u=\sin t\\ \mathrm{d} u=\cos t\, \mathrm{d} t \end{matrix}\right\bracevert = \displaystyle\int\left(1-u^2\right)\,\mathrm{d} u=
    =u-\dfrac{u^3}{3}+C=\sin t-\dfrac{\sin^3t}{3}+C.
Příklad č. 448» Zobrazit zadání «

Najděte vzorec pro výpočet objemu komolého kužele s poloměrem podstav r_1, r_2 a výškou v.

Jaký je objem „nekomolého“ kužele?

Řešení» Zobrazit řešení «

Komolý kužel lze vytvořit tak, že necháme rotovat lichoběžník s vrcholy

[0,0], \quad [v,0], \quad [v,r_2], \quad [0,r_1]

kolem osy x.

Graf

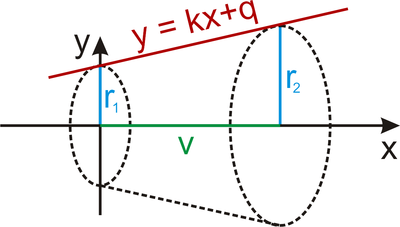
K výpočtu ovšem potřebujeme funkční předpis přímky dané body [0,r_1] a [v,r_2]. Ten najdeme ve směrnicovém tvaru y=kx+q. Dosazením bodu [0,r_1] do rovnice přímky ihned dostaneme, že q=r_1. Pomocí této znalosti a dosazením bodu [v,r_2] do rovnice přímky dostaneme směrnici k = \tfrac{r_2-r_1}{v}. Úsečka, jejíž rotací vznikne plášť studovaného komolého kužele je tedy dána předpisem

y = \dfrac{r_2-r_1}{v} x + r_1, \qquad x \in [0,v].

Nyní použijeme známý vzorec

V_x = \pi \displaystyle\int\limits_0^{v} \left(\dfrac{r_2-r_1}{v} x + r_1\right)^2 \mathrm{d} t.

Umocním závorky a jednoduchou integrací polynomu obdržíme výsledek

V = \dfrac{1}{3} \pi v (r_1^2+r_1r_2+r_2^2).

Obyčejný kužel je speciální případ kužele komolého s nulovým poloměrem jedné podstavy. Tedy položíme-li např. r_1=0, r_2=r, získáme vzorec pro objem „obyčejného“ kužele ve tvaru

V_K = \dfrac{1}{3} \pi r^2 v.

Příklad č. 449» Zobrazit zadání «

Určete obsah pláště tělesa, které vznikne rotací podgrafu funkce f(x)=2 \lvert \sin x \rvert, x\in[0,2\pi], kolem osy x.

Řešení» Zobrazit řešení «

Graf

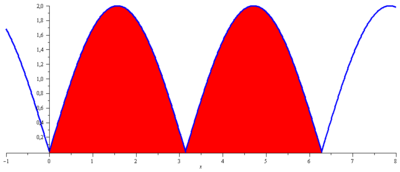
Oba oblouky sinusoidy jsou stejné, můžeme se omezit pouze na interval [0,\pi], proto

Q_x =2\cdot2\pi\displaystyle\int\limits_{0}^{2\pi}\left(2\sin x\sqrt{1+4\cos^2 x}\right)\mathrm{d} x \left\bracevert\begin{matrix} 2\cos x=t\\ -2\sin x\,\mathrm{d} x=\mathrm{d} t\\ 0\rightsquigarrow2\\ \pi\rightsquigarrow-2 \end{matrix}\right\bracevert =
= -4\pi\displaystyle\int{2}^{-2}\sqrt{1+t^2}\,\mathrm{d} t=8\displaystyle\int\limits_{0}^{2}\sqrt{1+t^2}\,\mathrm{d} t=
=8\pi\left[\dfrac{1}{2}\ln \lvert t+\sqrt{1+t^2} \rvert +\dfrac{t}{2}\sqrt{1+t^2}\right]_{0}^{2}=
= 8\left(\dfrac{1}{2}\ln\left(2+\sqrt{5}\right)+\sqrt{5}\right)= 4\pi\ln(2+\sqrt{5})+8\pi\sqrt{5}.

Při výpočtu jsme využili následující výpočet primitivní funkce

\displaystyle\int\sqrt{1+t^2}\,\mathrm{d} t \left\bracevert\begin{matrix} t=\sinh u\\ \mathrm{d} t=\cosh u\,\mathrm{d} u \end{matrix}\right\bracevert =\displaystyle\int\cosh^2u\,\mathrm{d} u \left\bracevert\begin{matrix} \cosh2u=2\cosh^2u-1 \end{matrix}\right\bracevert =
\hspace*{5mm}= \dfrac{1}{2}\displaystyle\int\dfrac{\cosh2u+1}{2}\,\mathrm{d} u=\dfrac{1}{2}\left(\dfrac{\sinh 2u}{2}+u\right)+C=
\hspace*{5mm}= \dfrac{\sinh u\,\cosh u}{2}+\dfrac{u}{2}+C \left\bracevert\begin{matrix} \cosh^2u-\sinh^2=1\Rightarrow\cosh u=\sqrt{\sinh^2u+1} \end{matrix}\right\bracevert =
\hspace*{5mm}= \dfrac{t\sqrt{t^2+1}}{2}+\dfrac{\operatorname{argsinh} t}{2}+C.

Navíc přímým výpočtem ověříme, že

\operatorname{argsinh} t=\ln \bigl\lvert t+\sqrt{t^2+1} \bigr\rvert .

Položme \sinh x=\frac{\operatorname{e}^{x}-\operatorname{e}^{-x}}{2} = y,  potom

\ln \bigl\lvert y+\sqrt{y^2+1} \bigr\rvert =\ln \Biggl\lvert \dfrac{\operatorname{e}^{x}-\operatorname{e}^{-x}}{2}+\sqrt{\dfrac{\operatorname{e}^{2x}-2+\operatorname{e}^{-2x}}{4}+1} \Biggr\rvert =
= \ln \Biggl\lvert \dfrac{\operatorname{e}^{x}-\operatorname{e}^{-x}}{2}+\sqrt{\dfrac{\operatorname{e}^{2x}+\operatorname{e}^{-2x}+2}{4}} \Biggr\rvert =
= \ln \Biggl\lvert \dfrac{\operatorname{e}^{x}-\operatorname{e}^{-x}}{2}+\sqrt{\dfrac{\left(\operatorname{e}^{x}+\operatorname{e}^{-x}\right)^2}{4}} \Biggr\rvert =
= \ln \biggl\lvert \dfrac{\operatorname{e}^{x}-\operatorname{e}^{-x}}{2}+\dfrac{\operatorname{e}^{x}+\operatorname{e}^{-x}}{2} \biggr\rvert =\ln \lvert \operatorname{e}^{x} \rvert =x=\operatorname{argsinh} y.
Příklad č. 450» Zobrazit zadání «

Určete obsah pláště tělesa, které vznikne rotací podgrafu funkce f(x)=4+x, x\in[-4,2], kolem osy x.

Řešení» Zobrazit řešení «
Q_x =2\pi\displaystyle\int\limits_{-4}^{2}(4+x)\sqrt{1+1}\,\mathrm{d} x=2\sqrt{2}\pi\displaystyle\int\limits_{-4}^{2}\left(4+x\right)\,\mathrm{d} x=
= 2\sqrt{2}\pi\left[4x+\dfrac{x^2}{2}\right]_{-4}^{2}=2\sqrt{2}\pi\left(8+\dfrac{4}{2}\-16-\dfrac{16}{2}\right)= 36\sqrt{2}\pi.
Příklad č. 451» Zobrazit zadání «

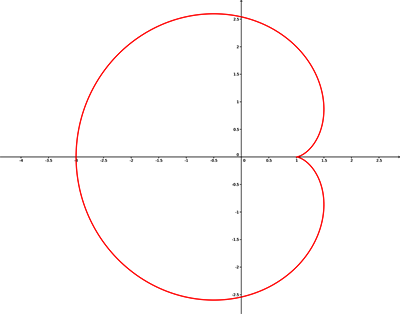
Určete obsah pláště tělesa, které vznikne rotací kardioidy (srdcovky) x=2\cos t-\cos2t, y=2\sin t-\sin2t, t\in[0,\pi], kolem osy x.

Řešení» Zobrazit řešení «

Graf

Q_x =2\pi\displaystyle\int\limits_{0}^{\pi}\left(2\sin t-\sin2t\right)\sqrt{\left(-2\sin t+2\sin 2t\right)^2+\left(2\cos t-2\cos 2t\right)^2}\,\mathrm{d} t=
= 2\pi\displaystyle\int\limits_{0}^{\pi}\left(2\sin t-\sin2t\right)\sqrt{8}\sqrt{-\sin t\sin 2t-\cos t\cos 2t}\,\mathrm{d} t
\hspace{5mm} \left\bracevert\begin{matrix} \sin 2t=2\sin t\cos t\\ \cos 2t=\cos^2t-\sin^2t \end{matrix}\right\bracevert =
= 2\pi\displaystyle\int\limits_{0}^{\pi}\left(2\sin t-\sin2t\right)\sqrt{8}\sqrt{1-\cos t}\,\mathrm{d} t=
=2\sqrt{8}\pi\displaystyle\int\limits_{0}^{\pi}2\sin t\left(1-\cos t\right)^{3/2}\mathrm{d} t=
= 4\sqrt{8}\pi\displaystyle\int\limits_{0}^{\pi}\sin t\left(1-\cos t\right)^{\frac{3}{2}}\,\mathrm{d} t \left\bracevert\begin{matrix} u=1-\cos t\\ \mathrm{d} u=\sin t\,\mathrm{d} t\\ 0\rightsquigarrow0\\ \pi\rightsquigarrow2 \end{matrix}\right\bracevert = 4\sqrt{8}\pi\displaystyle\int\limits_{0}^{2}2u^{\frac{3}{2}}\,\mathrm{d} u=
= 4\sqrt{8}\pi\left[\dfrac{u^{\frac{5}{2}}}{\frac{5}{2}}\right]_{0}^{2}= 4\sqrt{8}\pi\left(\dfrac{2^{\frac{5}{2}}}{\frac{5}{2}}\right)= 4\sqrt{8}\pi\dfrac{2}{5}4\sqrt{2}=\dfrac{128}{5}\pi.
Příklad č. 452» Zobrazit zadání «

Určete obsah pláště tělesa, které vznikne rotací prvního oblouku cykoidy x=t-\sin t, y=1-\cos t, t\in[0,2\pi], kolem osy x.

Řešení» Zobrazit řešení «
Q_x =2\pi\displaystyle\int\limits_{0}^{2\pi}(1-\cos t)\sqrt{(1-\cos t)^2+\sin^2 t}\,\mathrm{d} t=
= 2\pi\displaystyle\int\limits_{0}^{2\pi}(1-\cos t)\sqrt{2}\sqrt{1-\cos t}\,\mathrm{d} t=
=2\sqrt{2}\pi\displaystyle\int\limits_{0}^{2\pi}(1-\cos t)^{3/2}\,\mathrm{d} t \left\bracevert\begin{matrix} 1-\cos t=\sin^2\dfrac{t}{2} \end{matrix}\right\bracevert =
= 2\sqrt{2}\pi\displaystyle\int\limits_{0}^{2\pi}2\sqrt{2}\sin^3\dfrac{t}{2}\,\mathrm{d} t= 8\pi\displaystyle\int\limits_{0}^{2\pi}\left(1-\cos^2\dfrac{t}{2}\right)\sin\dfrac{t}{2}\,\mathrm{d} t \left\bracevert\begin{matrix} \cos\dfrac{t}{2}=u\\ \dfrac{1}{2}\,\sin\dfrac{t}{2}\,\mathrm{d} t=\mathrm{d} u \vspace{2mm}\\ 0\rightsquigarrow1\vspace{2mm}\\ 2\pi\rightsquigarrow-1 \end{matrix}\right\bracevert =
= -8\pi2\displaystyle\int\limits_{1}^{-1}\left(1-u^2\right)\,\mathrm{d} u= 16\pi\left[u-\dfrac{u^3}{3}\right]_{-1}^{1}= 16\pi\left(1-\dfrac{1}{3}+1-\dfrac{1}{3}\right)=\\ =\dfrac{64}{3}\pi.
Příklad č. 453» Zobrazit zadání «

Vypočtěte souřadnice těžiště homogenní půlkružnice x^2+y^2=r^2, y\geq0.

Řešení» Zobrazit řešení «

Podle příslušných vzorců obdržíme

M =\sigma\displaystyle\int\limits_{0}^{\pi}\sqrt{\left(-r\sin t\right)^2+\left(r\cos t\right)^2}\,\mathrm{d} t= \sigma r\displaystyle\int\limits_{0}^{\pi}\,\mathrm{d} t=\pi\sigma r,
S_{x} =\sigma\displaystyle\int\limits_{0}^{\pi}r\sin t\sqrt{\left(-r\sin t\right)^2+\left(r\cos t\right)^2}\,\mathrm{d} t=
=\sigma r^2\displaystyle\int\limits_{0}^{\pi}\sin t\,\mathrm{d} t=\sigma r^2\left[-\cos t\right]_{0}^{\pi}=2\sigma r^2,
S_{y} =\sigma\displaystyle\int\limits_{0}^{\pi}r\cos t\sqrt{\left(-r\sin t\right)^2+\left(r\cos t\right)^2}\,\mathrm{d} t=
=\sigma r^2\displaystyle\int\limits_{0}^{\pi}\cos t\,\mathrm{d} t=\sigma r^2\left[\sin t\right]_{0}^{\pi}=0.

Proto souřadnice těžiště jsou

T=\left[\dfrac{0}{\pi \sigma r},\dfrac{2\sigma r^2}{\pi \sigma r}\right]=\left[0,\dfrac{2r}{\pi}\right].

Příklad č. 454» Zobrazit zadání «

Vypočtěte hmotnost a souřadnice těžiště křivky x=a\cos^3 t, y=a\sin^3 t, a>0, x,y\geq0, kde délková hustota v bodě s(x) v bodě [x(t),y(t)] je přímo úměrná x –ové souřadnici bodu.

Řešení» Zobrazit řešení «

Podle příslušných vzorců obdržíme

M =\displaystyle\int\limits_{0}^{\frac{\pi}{2}}k a\cos^3t\sqrt{\left(3a\cos^2t\left(-\sin t\right)^2\right)+\left(3a\sin^2 t\cos t\right)^2}\,\mathrm{d} t=
= \displaystyle\int\limits_{0}^{\frac{\pi}{2}}k a\cos^3t\sqrt{9a^2\cos^4t\sin^2t+9a^2\sin^4t\cos^2t}\,\mathrm{d} t=
= \displaystyle\int\limits_{0}^{\frac{\pi}{2}}k a\cos^3t\sqrt{\cos^2 t\sin^2 t\left(\cos^2 t+\sin^2 t\right)}\,\mathrm{d} t=
= 3ka^2\displaystyle\int\limits_{0}^{\frac{\pi}{2}}\cos^4 t\sin t\,\mathrm{d} t \left\bracevert\begin{matrix} \cos t=u\\ -\sin t\,\mathrm{d} t=\mathrm{d} u\\ \dfrac{\pi}{2}\rightsquigarrow0\\ 0\rightsquigarrow1 \end{matrix}\right\bracevert = -3ka^2\displaystyle\int\limits_{1}^{0}u^4\,\mathrm{d} u=
=-3ka^2\left[\dfrac{u^5}{5}\right]_{1}^{0}= -3ka^2\left(0-\dfrac{1}{5}\right)=\dfrac{3ka^2}{5},
S_{x} =\displaystyle\int\limits_{0}^{\frac{\pi}{2}}3ka^3\cos^4t\sin^4t\,\mathrm{d} t=3ka^3\left[-\dfrac{1}{128}\sin4t+\dfrac{3}{128}t+\dfrac{1}{1024}\sin8t\right]_{0}^{\frac{\pi}{2}}=
= 3ka^3\dfrac{3}{128}\dfrac{\pi}{2}=3ka^3\dfrac{3\pi}{256},

kde jsme využili následující primitivní funkce

  1. \displaystyle\int\cos^2t\,\mathrm{d} t=\dfrac{t}{2}+\dfrac{\sin 2t}{4}+C,
  2. \displaystyle\int\cos^2 2t\,\mathrm{d} t \left\bracevert\begin{matrix} 2t=u\ 3\,\mathrm{d} t=\mathrm{d} u \end{matrix}\right\bracevert \dfrac{1}{2}\displaystyle\int\cos^2u\,\mathrm{d} u=\dfrac{1}{2}\left(\dfrac{u}{2}+\dfrac{\sin 2u}{4}\right)+C=\ \hspace*{6mm} = \dfrac{t}{2}+\dfrac{\sin 4t}{8}+C,
  3. \displaystyle\int\sin^4t\cos^4t\,\mathrm{d} t \left\bracevert\begin{matrix} \cos 2t=2\cos^2t-1 \end{matrix}\right\bracevert =
    \hspace*{6mm}=\dfrac{1}{16}\displaystyle\int\left(1-\cos2t\right)^2\left(1\cos2t\right)^2\,\mathrm{d} t=
    \hspace*{6mm}= \dfrac{1}{16}\displaystyle\int\left(1-2\cos^2 2t+\cos^4 2t\right)\,\mathrm{d} t \left\bracevert\begin{matrix} 2t=u\\ 3\,\mathrm{d} t=\mathrm{d} u \end{matrix}\right\bracevert =
    \hspace*{6mm}=\dfrac{1}{16}\left(t-t-\dfrac{\sin 4t}{4}+\dfrac{1}{2}\displaystyle\int\cos^4 u\,\mathrm{d} u\right)=
    \hspace*{6mm}= -\dfrac{1}{64}\sin4t+\dfrac{1}{32}\displaystyle\int\dfrac{1}{4}\left(1+\cos 2u\right)^2\,\mathrm{d} u=
    \hspace*{6mm}=-\dfrac{1}{64}\sin4t+\dfrac{1}{128}\displaystyle\int\left(1+2\cos 2u+\cos^2 2u\right)\,\mathrm{d} u=
    \hspace*{6mm}= -\dfrac{1}{64}\sin4t+\dfrac{1}{128}u+\dfrac{1}{64}\dfrac{1}{2}\sin2u+\dfrac{1}{128}\left(\dfrac{u}{2}+\dfrac{\sin 4u}{8}\right)+C=
    \hspace*{6mm}= \dfrac{3}{128}t-\dfrac{1}{128}\sin4t+\dfrac{1}{1028}\sin 8t+C.

Dále platí

S_{y} =\displaystyle\int\limits_{0}^{\frac{\pi}{2}}3ka^3\cos^7t\sin t\,\mathrm{d} t \left\bracevert\begin{matrix} u=\cos t\\ \mathrm{d} u=-\sin t\,\mathrm{d} t\\ 0\rightsquigarrow1\\ \dfrac{\pi}{2}\rightsquigarrow0 \end{matrix}\right\bracevert =
=-3ka^3\displaystyle\int\limits_{1}^{0}u^7\,\mathrm{d} u=-3ka^3\left[\dfrac{u^8}{8}\right]_{1}^{0}=\dfrac{3ka^3}{8}.

Proto těžiště má souřadnice

T=\left[\dfrac{3ka^3}{8}\,\dfrac{5}{3ka^2},3ka^3\dfrac{3\pi}{256}\,\dfrac{5}{3ka^2}\right]= \left[\dfrac{5a}{8},\dfrac{15\pi a}{256}\right].

Příklad č. 455» Zobrazit zadání «

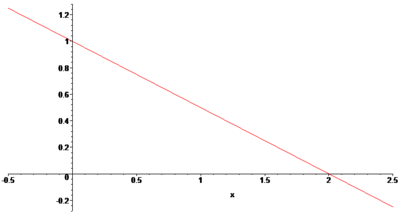
Vypočtěte souřadnice těžiště trojúhelníku s vrcholy O=[0,0], A=[0,1] a B=[2,0].

Řešení» Zobrazit řešení «

Graf

M =\sigma\displaystyle\int\limits_{0}^{2}\left(1-\dfrac{x}{2}\right)\,\mathrm{d} x=\sigma\left[x-\dfrac{x^2}{4}\right]=\sigma\left(2-1\right)=\sigma,
S_{x} =\dfrac{1}{2}\sigma\displaystyle\int\limits_{0}^{2}\left(1-\dfrac{x}{2}\right)^2\,\mathrm{d} x= \dfrac{1}{2}\sigma\displaystyle\int\limits_{0}^{2}\left(1-x+\dfrac{x^2}{4}\right)\,\mathrm{d} x=
= \dfrac{1}{2}\sigma\left[x-\dfrac{x^2}{2}+\dfrac{x^3}{12}\right]_{0}^{2}= \dfrac{1}{2}\sigma\left(2-2+\dfrac{8}{12}\right)=\dfrac{\sigma}{3},
S_{y} =\sigma\displaystyle\int\limits_{0}^{2}x\left(1-\dfrac{x}{2}\right)\,\mathrm{d} x= \sigma\displaystyle\int\limits_{0}^{2}\left(x-\dfrac{x^2}{2}\right)\,\mathrm{d} x= \sigma\left[\dfrac{x^2}{2}-\dfrac{x^3}{6}\right]_{0}^{2}=
= \sigma\left(2-\dfrac{8}{6}\right)=\dfrac{2}{3}\sigma.

Souřadnice těžiště tedy jsou

T=\left[\dfrac{2}{3},\dfrac{1}{3}\right].

Příklad č. 456» Zobrazit zadání «

Vypočtěte hmotnost a souřadnice těžiště rovinné homogenní plochy omezené křivkou y=2\sin 3x, x=0, x=\frac{\pi}{3} a osou x.

Řešení» Zobrazit řešení «
M =\sigma\displaystyle\int\limits_{0}^{\frac{\pi}{3}}2\sin 3x\,\mathrm{d} x=\dfrac{2}{3}\sigma\left[-\cos 3x\right]_{0}^{\frac{\pi}{3}}=\dfrac{4}{3}\sigma,
S_{x} =\dfrac{1}{2}\sigma\displaystyle\int\limits_{0}^{\frac{\pi}{3}}4\sin^2 3x\,\mathrm{d} x= 2\sigma\left[\dfrac{x}{2}-\dfrac{\sin 6x}{12}\right]=\dfrac{\sigma\pi}{3},
S_{y} =\sigma\displaystyle\int\limits_{0}^{\frac{\pi}{3}}x2\sin 3x\,\mathrm{d} x= \dfrac{2}{9}\sigma\left[\sin 3x-3x\cos 3x\right]_{0}^{\frac{\pi}{3}}=\dfrac{2\sigma\pi}{9},

kde jsme využili

  1. \displaystyle\int\sin^2 3x\,\mathrm{d} x \left\bracevert\begin{matrix} t=3x\\ \mathrm{d} t=3\,\mathrm{d} x \end{matrix}\right\bracevert =\dfrac{1}{3}\displaystyle\int\sin^2t\,\mathrm{d} t=\dfrac{1}{3}\displaystyle\int\left(\dfrac{1}{2}-\dfrac{1}{2}\cos2t\right)\,\mathrm{d} t=
    \hspace*{5mm}= \dfrac{t}{6}-\dfrac{\sin 2t}{12}+C=\dfrac{x}{2}-\dfrac{\sin 6x}{12}+C,
  2. \displaystyle\int x\sin3x\,\mathrm{d} x \left\bracevert\begin{matrix} u=x & u'=1\\ v=-\dfrac{1}{3}\cos3x & v'=\sin 3x \end{matrix}\right\bracevert = \\ \hspace*{5mm} = -\dfrac{1}{3}x\cos 3x+\dfrac{1}{3}\displaystyle\int\cos 3x\,\mathrm{d} x=
    \hspace*{5mm}= -\dfrac{1}{3}x\cos 3x+\dfrac{1}{9}\sin 3x+C= \dfrac{1}{9}\left(\sin 3x-3x\cos 3x\right)+C.

Proto těžiště souřadnice jsou dány

T=\left[\dfrac{2\sigma\pi}{9}\dfrac{3}{4\sigma},\dfrac{\sigma\pi}{3}\dfrac{3}{4\sigma}\right]=\left[\dfrac{\pi}{6},\dfrac{\pi}{4}\right].

Příklad č. 457» Zobrazit zadání «

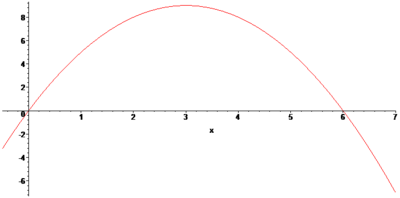
Vypočtěte souřadnice těžiště rovinného obrazce ohraničeného křivkou danou předpisem y=6x-x^2 a osou x.

Řešení» Zobrazit řešení «

Graf

M =\sigma\displaystyle\int\limits_{0}^{6}\left(6x-x^2\right)\,\mathrm{d} x=\sigma\left[3x^2-\dfrac{x^3}{3}\right]_{0}^{6}=\sigma\left(108-2\cdot 36\right)=36\sigma,
S_{x} =\dfrac{1}{2}\sigma\displaystyle\int\limits_{0}^{6}\left(6x-x^2\right)^2\,\mathrm{d} x=\dfrac{1}{2}\sigma\displaystyle\int\limits_{0}^{6}\left(36x^2-12x^3+x^4\right)\,\mathrm{d} x=
=\dfrac{1}{2}\sigma\left[\dfrac{36x^3}{3}-\dfrac{12x^4}{4}+\dfrac{x^5}{5}\right]_{0}^{6}=\dfrac{648}{5}\sigma,
S_{y} =\sigma\displaystyle\int\limits_{0}^{6}x\left(6x-x^2\right)\,\mathrm{d} x=\sigma\displaystyle\int\limits_{0}^{6}\left(6x^2-x^3\right)\,\mathrm{d} x= \sigma\left[\dfrac{6x^3}{3}-\dfrac{x^4}{4}\right]_{0}^{6}=108\sigma.

Těžiště má tedy souřadnice

T=\left[3,\dfrac{18}{5}\right].

Příklad č. 458» Zobrazit zadání «

Vypočtěte souřadnice těžiště rovinného obrazce ohraničeného cykloidou x=3(t-\sin t), y=3(1-\cos t), 0\leq t \leq 2\pi a osou x.

Řešení» Zobrazit řešení «
M =\sigma\displaystyle\int\limits_{0}^{2\pi}3\left(1-\cos t\right)3\left(1-\cos t\right)\,\mathrm{d} t=
=9\sigma\displaystyle\int\limits_{0}^{2\pi}\left(1-\cos t\right)^2\,\mathrm{d} t\overset{\text{Př. }(438)}{=}9\sigma4\pi=27\sigma\pi,
S_{x} =\dfrac{1}{2}\sigma\displaystyle\int\limits_{0}^{2\pi}9\left(1-\cos t\right)^2 3\left(1-\cos t\right)\,\mathrm{d} t= \dfrac{27}{2}\sigma\displaystyle\int\limits_{0}^{2\pi}\left(1-\cos t\right)^3\,\mathrm{d} t=
= \dfrac{27}{2}\sigma\displaystyle\int\limits_{0}^{2\pi}\left(1-3\cos t+3\cos^2 t-\cos^3 t\right)\,\mathrm{d} t\overset{\text{ Př. }(447)}{=}
\hspace{-9mm}\overset{\hspace{9mm}\text{Př. }(447)}{=}\dfrac{27}{2}\sigma\left[t-3\sin t+\dfrac{3}{2}\left(\cos t\cdot\sin t+t\right)-\sin t- \dfrac{\sin^3 t}{3}\right]_{0}^{2\pi}=
=\dfrac{27}{2}\sigma\left(5\pi\right)=\dfrac{135}{2}\pi\sigma,
S_{y} =\sigma\displaystyle\int\limits_{0}^{2\pi}3(t-\sin t)3\left(1-\cos t\right) 3\left(1-\cos t\right)\,\mathrm{d} t=
= 27\sigma\displaystyle\int\limits_{0}^{2\pi}\left(1-2\cos t+\cos^2 t\right)(t-\sin t)\,\mathrm{d} t=
= 27\sigma\displaystyle\int\limits_{0}^{2\pi}\left(t-\sin t-2t\cos t+2\cos t\sin t+t\cos^2t-\cos^2t\sin t\right)\,\mathrm{d} t=
= 27\sigma\bigg[\dfrac{t^2}{2}+\cos t-2t\sin t-2\cos t-\cos^2t+\dfrac{t}{2}\left(\cos t\cdot\sin t+t\right)-
\hspace*{15mm}- \dfrac{t}{2}\left(-\dfrac{\cos^2t}{2}+\dfrac{t^2}{2}\right)-\dfrac{\cos^3t}{3}\bigg]_{0}^{2\pi}=
= 27\sigma\left(2\pi^2+2\pi^2+\dfrac{1}{4}-\pi^2-\dfrac{1}{4}\right)=
=27\sigma3\pi^2,

k čemuž jsme v posledním integrálu využili

  1. \displaystyle\int t\cos^2t\,\mathrm{d} t \left\bracevert\begin{matrix} u=t & u'=1\\ v\overset{\text{Př. }(447)}{=}\dfrac{1}{2}\left(\cos t\cdot \sin t+t\right) & v'=\cos^2 t \end{matrix}\right\bracevert =
    \hspace*{5mm}= \dfrac{1}{2}\left(\cos t\cdot \sin t+t\right)-\dfrac{1}{2}\displaystyle\int\left(\cos t\cdot \sin t+t\right)\,\mathrm{d} t=
    \hspace*{5mm}= \dfrac{1}{2}\left(\cos t\cdot \sin t+t\right)-\dfrac{1}{2}\left(-\dfrac{\cos^2t}{2}-\dfrac{t^2}{2}\right)+C,
  2. \displaystyle\int t\cos t\,\mathrm{d} t \left\bracevert\begin{matrix} u=t & u'=1\\ v=\sin t & v'=\cos t \end{matrix}\right\bracevert =t\sin t-\displaystyle\int\sin t\,\mathrm{d} t=
    \hspace*{5mm}=t\sin t+\cos t+C,
  3. \displaystyle\int\cos t\sin t\,\mathrm{d} t \left\bracevert\begin{matrix} u=\cos t\\ \mathrm{d} u=-\sin t\,\mathrm{d} t \end{matrix}\right\bracevert =-\displaystyle\int u\,\mathrm{d} u=-\dfrac{u^2}{2}+C=-\dfrac{\cos^2 t}{2}+C,
  4. \displaystyle\int\cos^2t\sin t\,\mathrm{d} t \left\bracevert\begin{matrix} u=\cos t\\ \mathrm{d} u=-\sin t\mathrm{d} t \end{matrix}\right\bracevert =-\displaystyle\int u^2\,\mathrm{d} u=-\dfrac{u^3}{3}+C=-\dfrac{\cos^3 t}{3}.

Proto souřadnice těžiště jsou dány

T=T=\left[\dfrac{27\sigma 3\pi^2}{27\sigma\pi},\dfrac{135\pi\sigma}{2\cdot 27\sigma\pi}\right]=\left[3\pi,\dfrac{5}{2}\right].


nahoru

Tisková verze

Kapitola ve formátu PDF (Adobe Acrobat)

Mgr. Petr Zemánek, Ph.D., Mgr. Petr Hasil, Ph.D. |
ÚMS, Přírodovědecká fakulta, Masarykova univerzita |
Návrat na úvodní stránku webu, přístupnost |
Stránky Přírodovědecké fakulty MU
| Technická spolupráce:
| Servisní středisko pro e-learning na MU
| Fakulta informatiky Masarykovy univerzity, 2012

Technické řešení této výukové pomůcky je spolufinancováno Evropským sociálním fondem a státním rozpočtem České republiky.