Přírodovědecká fakulta Masarykovy univerzity
Mgr. Petr Zemánek, Ph.D., Mgr. Petr Hasil, Ph.D.
I. 1. Opakování a úvod do matematické analýzy
Základní vzorce
Mnohočleny
|
|
|
|
|
|
|
|
Mocninná funkce
|
|
|
|
|
|
|
|
Logaritmus a exponenciála
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Goniometrické funkce
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Zlomky
|
|
|
|
|
|
|
|
|
|
|
|
Ostatní
-
Komplexní čísla (
 )
)



-
Kvadratický polynom




-
Doplnění na čtverec


Reálná čísla
-
 pro každé
pro každé
 ;
;
-
je-li
 takové, že
takové, že
 pro každé
pro každé
 , pak je
, pak je
 .
.
Je-li
![]() , pak je
, pak je
![]() největším prvkem množiny
největším prvkem množiny
![]() , tj. pro každý prvek
, tj. pro každý prvek
![]() platí
platí
![]() . Analogické tvrzení platí pro
. Analogické tvrzení platí pro
![]() .
.
Kvadratické rovnice
Rovnice tvaru
![]() kde
kde
![]() nebo
nebo
![]() . Řešíme pomocí vzorců
. Řešíme pomocí vzorců
![]()
-
 různé reálné kořeny,
různé reálné kořeny,
-
 dvojnásobný reálný kořen,
dvojnásobný reálný kořen,
-
 komplexně sdružené komplexní kořeny.
komplexně sdružené komplexní kořeny.
Posouvání grafu
Nechť je dána funkce
![]() a nenulová reálná čísla
a nenulová reálná čísla
![]() .
.
-
Uvažujme funkci
 . Tato funkce má vůči původní funkci graf posunutý buď doleva (je-li
. Tato funkce má vůči původní funkci graf posunutý buď doleva (je-li
 ) nebo doprava (je-li
) nebo doprava (je-li
 ), a to o velikost čísla
), a to o velikost čísla
 .
.
-
Uvažujme funkci
 . Tato funkce má vůči původní funkci graf posunutý buď nahoru (je-li
. Tato funkce má vůči původní funkci graf posunutý buď nahoru (je-li
 ) nebo dolů (je-li
) nebo dolů (je-li
 ), a to o velikost čísla
), a to o velikost čísla
 .
.
Určete (jestliže existují)
![]() ,
,
![]() ,
,
![]() a
a
![]() , kde
, kde
-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení « a
a
 ;
;
-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení « ,
,
 a
a
 neexistuje;
neexistuje;
-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení « a
a
 neexistuje,
neexistuje,
 ;
;
-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení « neexistuje,
neexistuje,
 a
a
 .
.
Dokažte následující tvrzení: „Buď
![]() ,
,
![]() a nechť
a nechť
![]() . Pak
. Pak
|
|
|
|
|
|
“ |
„![]() “
Buď
“
Buď
![]() , pak z definice
, pak z definice
![]() pro
pro
![]() , tj. platí 1). Předpokládejme, že 2) neplatí. Pak existuje
, tj. platí 1). Předpokládejme, že 2) neplatí. Pak existuje
![]() tak, že
tak, že
![]() je
je
![]() . Tedy
. Tedy
![]() je horní závora množiny
je horní závora množiny
![]() a zároveň
a zároveň
![]()
![]()
![]() , což je spor. Tedy 2) platí.
, což je spor. Tedy 2) platí.
„![]() “
Nechť platí 1) i 2). Podle definice určitě platí
“
Nechť platí 1) i 2). Podle definice určitě platí
![]() . Předpokládejme, že
. Předpokládejme, že
![]()
Potom položme
![]() . Z 2) plyne, že
. Z 2) plyne, že
![]()
což je spor. Proto nutně
![]() .
.
Za předpokladu existence daných výrazů dokažte:
-
![\sup\limits_{x\in A}[-f(x)]=-\inf\limits_{x\in A}[f(x)]; \sup\limits_{x\in A}[-f(x)]=-\inf\limits_{x\in A}[f(x)];](f.gif) Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «![\sup\limits_{x\in A}\left[-f(x)\right]=c\Rightarrow \sup\limits_{x\in A}\left[-f(x)\right]=c\Rightarrow](f.gif)
![\Rightarrow\left[-f(x)\leq c\ \forall x\in A\right]\wedge \left[\left(b\in\mathbb{R},\ -f(x)\leq b\ \forall x\in A\right) \Rightarrow c\leq b\right]\Rightarrow \Rightarrow\left[-f(x)\leq c\ \forall x\in A\right]\wedge \left[\left(b\in\mathbb{R},\ -f(x)\leq b\ \forall x\in A\right) \Rightarrow c\leq b\right]\Rightarrow](f.gif)
![\Rightarrow\left[f(x)\geq -c\ \forall x\in A\right]\wedge \left[\left(b\in\mathbb{R},\ f(x)\geq -b\ \forall x\in A\right) \Rightarrow -c\geq -b\right]\Rightarrow \Rightarrow\left[f(x)\geq -c\ \forall x\in A\right]\wedge \left[\left(b\in\mathbb{R},\ f(x)\geq -b\ \forall x\in A\right) \Rightarrow -c\geq -b\right]\Rightarrow](f.gif)
![\Rightarrow\inf\limits_{x\in A}\left[f(x)\right]=-c \Rightarrow \sup\limits_{x\in A}\left[-f(x)\right]=c=-\inf\left[f(x)\right]. \Rightarrow\inf\limits_{x\in A}\left[f(x)\right]=-c \Rightarrow \sup\limits_{x\in A}\left[-f(x)\right]=c=-\inf\left[f(x)\right].](f.gif)
-
![\inf\limits_{x\in A}[-f(x)]=-\sup\limits_{x\in A}[f(x)]; \inf\limits_{x\in A}[-f(x)]=-\sup\limits_{x\in A}[f(x)];](f.gif) Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «![\inf\limits_{x\in A}\left[-f(x)\right]=c\Rightarrow \inf\limits_{x\in A}\left[-f(x)\right]=c\Rightarrow](f.gif)
![\Rightarrow\left[-f(x)\geq c\ \forall x\in A\right]\wedge \left[\left(b\in\mathbb{R},\ -f(x)\geq b\ \forall x\in A\right) \Rightarrow c\geq b\right]\Rightarrow \Rightarrow\left[-f(x)\geq c\ \forall x\in A\right]\wedge \left[\left(b\in\mathbb{R},\ -f(x)\geq b\ \forall x\in A\right) \Rightarrow c\geq b\right]\Rightarrow](f.gif)
![\Rightarrow\left[f(x)\leq -c\ \forall x\in A\right]\wedge \left[\left(b\in\mathbb{R},\ f(x)\leq -b\ \forall x\in A\right) \Rightarrow -c\leq -b\right]\Rightarrow \Rightarrow\left[f(x)\leq -c\ \forall x\in A\right]\wedge \left[\left(b\in\mathbb{R},\ f(x)\leq -b\ \forall x\in A\right) \Rightarrow -c\leq -b\right]\Rightarrow](f.gif)
![\Rightarrow\sup\limits_{x\in A}\left[f(x)\right]=-c \Rightarrow \inf\limits_{x\in A}\left[-f(x)\right]=c=-\sup\left[f(x)\right]. \Rightarrow\sup\limits_{x\in A}\left[f(x)\right]=-c \Rightarrow \inf\limits_{x\in A}\left[-f(x)\right]=c=-\sup\left[f(x)\right].](f.gif)
-
![\sup\limits_{x\in A}[f(x)+g(x)]\leq\sup\limits_{x\in A}[f(x)]+\sup\limits_{x\in A}[g(x)]; \sup\limits_{x\in A}[f(x)+g(x)]\leq\sup\limits_{x\in A}[f(x)]+\sup\limits_{x\in A}[g(x)];](f.gif) Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «

![\hspace{15mm}\Rightarrow \sup\limits_{x\in A}\left[f(x)+g(x)\right]\leq \sup\limits_{x\in A}\left[\sup\limits_{x\in A}f(x)+\sup\limits_{x\in A}g(x)\right] \hspace{15mm}\Rightarrow \sup\limits_{x\in A}\left[f(x)+g(x)\right]\leq \sup\limits_{x\in A}\left[\sup\limits_{x\in A}f(x)+\sup\limits_{x\in A}g(x)\right]](f.gif)
![\hspace{15mm}\Rightarrow \sup\limits_{x\in A}\left[f(x)+g(x)\right]\leq \sup\limits_{x\in A}f(x)+\sup\limits_{x\in A}g(x). \hspace{15mm}\Rightarrow \sup\limits_{x\in A}\left[f(x)+g(x)\right]\leq \sup\limits_{x\in A}f(x)+\sup\limits_{x\in A}g(x).](f.gif)
-
![\inf\limits_{x\in A}[f(x)+g(x)]\geq\inf\limits_{x\in A}[f(x)]+\inf\limits_{x\in A}[g(x)]; \inf\limits_{x\in A}[f(x)+g(x)]\geq\inf\limits_{x\in A}[f(x)]+\inf\limits_{x\in A}[g(x)];](f.gif) Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «

![\hspace{15mm}\Rightarrow \inf\limits_{x\in A}\left[f(x)+g(x)\right]\geq \inf\limits_{x\in A}\left[\inf\limits_{x\in A}f(x)+\inf\limits_{x\in A}g(x)\right] \hspace{15mm}\Rightarrow \inf\limits_{x\in A}\left[f(x)+g(x)\right]\geq \inf\limits_{x\in A}\left[\inf\limits_{x\in A}f(x)+\inf\limits_{x\in A}g(x)\right]](f.gif)
![\hspace{15mm}\Rightarrow \inf\limits_{x\in A}\left[f(x)+g(x)\right]\geq \inf\limits_{x\in A}f(x)+\inf\limits_{x\in A}g(x). \hspace{15mm}\Rightarrow \inf\limits_{x\in A}\left[f(x)+g(x)\right]\geq \inf\limits_{x\in A}f(x)+\inf\limits_{x\in A}g(x).](f.gif)
-
v částech iii) a iv) nelze nerovnosti nahradit rovnostmi.
Řešení» Zobrazit řešení «
Tvrzení dokážeme nalezením vhodného protipříkladu. Uvažujme např. funkce
 a
a
 na množině
na množině
![A=\left[0,\frac{\pi}{2}\right] A=\left[0,\frac{\pi}{2}\right]](f.gif) . Pak v iii) obdržíme
. Pak v iii) obdržíme
![\sup\limits_{x\in A}\left[\sin x+\cos x\right]=\sqrt{2}, \sup\limits_{x\in A}\left[\sin x+\cos x\right]=\sqrt{2},](f.gif)
přičemž
 a
a
 . V části iv) dostaneme
. V části iv) dostaneme
![\inf\limits_{x\in A}\left[\sin x+\cos x\right]=1, \inf\limits_{x\in A}\left[\sin x+\cos x\right]=1,](f.gif)
přičemž
 a
a
 .
.
Dokažte pro libovolné podmnožiny
![]() a
a
![]() množiny
množiny
![]() a libovolná reálná čísla
a libovolná reálná čísla
![]() ,
,
![]() ,
,
![]() :
:
-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «
![\Rightarrow \left[x\leq a\ \forall x\in M\right]\ \wedge\ a\in M\Rightarrow \Rightarrow \left[x\leq a\ \forall x\in M\right]\ \wedge\ a\in M\Rightarrow](f.gif)
![\Rightarrow\left[x\leq a\ \forall x\in M\right]\ \wedge \left[\left(b\in\mathbb{R},\ x\leq b\ \forall x\in M\right)\Rightarrow a\leq b\right]\Rightarrow \Rightarrow\left[x\leq a\ \forall x\in M\right]\ \wedge \left[\left(b\in\mathbb{R},\ x\leq b\ \forall x\in M\right)\Rightarrow a\leq b\right]\Rightarrow](f.gif)

-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «Označme
 a
a
 . Pak platí
. Pak platí

neboť
 .
.
-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «Označme
 a
a
 . Pak platí
. Pak platí

neboť
 .
.
-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «Označme
 ,
,
 ,
,
 a
a
 . Pak platí
. Pak platí
Také platí
![\Rightarrow x\in A\ \vee\ x\in B\Rightarrow \left[x\leq a\ \forall x\in A\right]\ \vee \left[x\leq b\ \forall x\in B\right]\Rightarrow \Rightarrow x\in A\ \vee\ x\in B\Rightarrow \left[x\leq a\ \forall x\in A\right]\ \vee \left[x\leq b\ \forall x\in B\right]\Rightarrow](f.gif)
![\Rightarrow\left[x\leq a\leq d\ \forall x\in A\right]\ \vee \left[x\leq b\leq d\ \forall x\in B\right]\Rightarrow \Rightarrow\left[x\leq a\leq d\ \forall x\in A\right]\ \vee \left[x\leq b\leq d\ \forall x\in B\right]\Rightarrow](f.gif)


To znamená, že

-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «Označme
 ,
,
 ,
,
 a
a
 . Pak platí
. Pak platí
Také platí
![\Rightarrow x\in A\ \vee\ x\in B\Rightarrow \left[x\geq a\ \forall x\in A\right]\ \vee \left[x\geq b\ \forall x\in B\right]\Rightarrow \Rightarrow x\in A\ \vee\ x\in B\Rightarrow \left[x\geq a\ \forall x\in A\right]\ \vee \left[x\geq b\ \forall x\in B\right]\Rightarrow](f.gif)
![\Rightarrow\left[x\geq a\geq d\ \forall x\in A\right]\ \vee \left[x\geq b\geq d\ \forall x\in B\right]\Rightarrow \Rightarrow\left[x\geq a\geq d\ \forall x\in A\right]\ \vee \left[x\geq b\geq d\ \forall x\in B\right]\Rightarrow](f.gif)


To znamená, že

-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «Označme
 ,
,
 ,
,
 a
a
 . Pak platí
. Pak platí

![\Rightarrow x\in A\ \wedge\ x\in B\Rightarrow \left[x\leq a\ \forall x\in A\right]\ \wedge \left[x\leq b\ \forall x\in B\right]\Rightarrow \Rightarrow x\in A\ \wedge\ x\in B\Rightarrow \left[x\leq a\ \forall x\in A\right]\ \wedge \left[x\leq b\ \forall x\in B\right]\Rightarrow](f.gif)
![\Rightarrow\left[x\leq a\ \forall x\in \left(A\cap B\right)\right]\ \vee \left[x\leq b\ \forall x\in \left(A\cap B\right)\right]\Rightarrow \Rightarrow\left[x\leq a\ \forall x\in \left(A\cap B\right)\right]\ \vee \left[x\leq b\ \forall x\in \left(A\cap B\right)\right]\Rightarrow](f.gif)

-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «Označme
 ,
,
 ,
,
 a
a
 . Pak platí
. Pak platí

![\Rightarrow x\in A\ \wedge\ x\in B\Rightarrow \left[x\geq a\ \forall x\in A\right]\ \wedge \left[x\geq b\ \forall x\in B\right]\Rightarrow \Rightarrow x\in A\ \wedge\ x\in B\Rightarrow \left[x\geq a\ \forall x\in A\right]\ \wedge \left[x\geq b\ \forall x\in B\right]\Rightarrow](f.gif)
![\Rightarrow\left[x\geq a\ \forall x\in \left(A\cap B\right)\right]\ \vee \left[x\geq b\ \forall x\in \left(A\cap B\right)\right]\Rightarrow \Rightarrow\left[x\geq a\ \forall x\in \left(A\cap B\right)\right]\ \vee \left[x\geq b\ \forall x\in \left(A\cap B\right)\right]\Rightarrow](f.gif)

-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «Pro
 platí
platí

Pro
 platí
platí

-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «Pro
 platí
platí

Pro
 platí
platí

-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «Z části viii) a ix) plyne


-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «Zvážíme všechny možné varianty. Pro
 a
a
 platí
platí

Pro
 a
a
 platí
platí

Pro
 a
a
 platí
platí

Pro
 a
a
 platí
platí

-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «Zvážíme všechny možné varianty. Pro
 a
a
 platí
platí

Pro
 a
a
 platí
platí

Pro
 a
a
 platí
platí

Pro
 a
a
 platí
platí

Dokažte:
-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «Pro
 je
je
 . Dále platí
. Dále platí
 pro všechna
pro všechna

-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «Platí
 pro
pro
 . Buď nyní
. Buď nyní
 libovolné. Zvolíme-li
libovolné. Zvolíme-li
 ,
,


-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «Platí
 pro
pro
 . Buď dále
. Buď dále
 libovolné. Zvolíme-li
libovolné. Zvolíme-li
 ,
,


-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «Platí
 pro
pro
 . Pro
. Pro
 platí
platí
 .
.
-




 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «Platí
 ,
,
 a
a
 . Z Příkladu 4 části iv) plyne
. Z Příkladu 4 části iv) plyne

![=\sup\left[\left(A\cup B\right)\cup C\right]= =\sup\left[\left(A\cup B\right)\cup C\right]=](f.gif)



Dokažte, že pro libovolné množiny
![]() ,
,
![]() a
a
![]() platí tzv.
distributivní zákony
platí tzv.
distributivní zákony
-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «











-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «









Určete množiny dané těmito výrazy:
-
![\left(1,\infty\right)\cap\left(-1,2\right]; \left(1,\infty\right)\cap\left(-1,2\right];](f.gif) Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «![\left(1,\infty\right)\cap\left(-1,2\right]=\left(1,2\right]; \left(1,\infty\right)\cap\left(-1,2\right]=\left(1,2\right];](f.gif)
-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «
-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «
-
![\left[ -1,5\right]\cap\left[ 5,100\right]; \left[ -1,5\right]\cap\left[ 5,100\right];](f.gif) Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «![\left[ -1,5\right]\cap\left[ 5,100\right]=\left\{5\right\}; \left[ -1,5\right]\cap\left[ 5,100\right]=\left\{5\right\};](f.gif)
-
![\left[ -1,10\right]\cap\left[ 15,20\right]; \left[ -1,10\right]\cap\left[ 15,20\right];](f.gif) Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «![\left[ -1,10\right]\cap\left[ 15,20\right]=\left\{\emptyset\right\}; \left[ -1,10\right]\cap\left[ 15,20\right]=\left\{\emptyset\right\};](f.gif)
-
 Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «
-
![\left[ 1,5\right)\setminus\left(0,5\right]. \left[ 1,5\right)\setminus\left(0,5\right].](f.gif) Řešení» Zobrazit řešení «
Řešení» Zobrazit řešení «![\left[ 1,5)\setminus(0,5\right]=\left\{\emptyset\right\}. \left[ 1,5)\setminus(0,5\right]=\left\{\emptyset\right\}.](f.gif)
Vyřešte kvadratickou rovnici
![]() a) v
a) v
![]() , b) v
, b) v
![]() .
.
Nejprve spočteme diskriminant dané rovnice
![]()
Protože
![]() , rovnice má dva reálné kořeny. Ty snadno dopočítáme.
, rovnice má dva reálné kořeny. Ty snadno dopočítáme.

Rovnice má tedy v
![]() dva kořeny a to
dva kořeny a to
![]() a
a
![]() , stejně jako v
, stejně jako v
![]() , neboť komplexní čísla jsou nadmnožinou čísel reálných.
, neboť komplexní čísla jsou nadmnožinou čísel reálných.
Vyřešte kvadratickou rovnici
![]() a) v
a) v
![]() , b) v
, b) v
![]() .
.
Nejprve spočteme diskriminant dané rovnice
![]()
Protože
![]() , rovnice má jeden dvojnásobný reálný kořen. Ten snadno dopočítáme.
, rovnice má jeden dvojnásobný reálný kořen. Ten snadno dopočítáme.
![]()
Rovnice má tedy v
![]() jeden dvojnásobný kořen a to
jeden dvojnásobný kořen a to
![]() , stejně jako v
, stejně jako v
![]() , neboť komplexní čísla jsou nadmnožinou čísel reálných.
, neboť komplexní čísla jsou nadmnožinou čísel reálných.
Vyřešte kvadratickou rovnici
![]() a) v
a) v
![]() , b) v
, b) v
![]() .
.
Nejprve spočteme diskriminant dané rovnice
![]()
Protože
![]() , rovnice nemá žádný reálný kořen – má dvojici komplexních kořenů. Ty dopočítáme.
, rovnice nemá žádný reálný kořen – má dvojici komplexních kořenů. Ty dopočítáme.
|
|
|

|
Rovnice tedy v
![]() nemá žádný kořen. V
nemá žádný kořen. V
![]() jsou jejími kořeny komplexně sdružená čísla
jsou jejími kořeny komplexně sdružená čísla
![]() a
a
![]() .
.
Určete, pro která
![]() je výraz
je výraz
![]() a) nezáporný, b) kladný.
a) nezáporný, b) kladný.
Protože jde o kvadratický polynom, je nejjednodušším způsobem načrtnout si jeho graf – parabolu. Jediné informace, které přitom musí být přesné, jsou průsečíky s osou
![]() (kořeny polynomu) a samozřejmě zda je parabola otevřena nahoru, nebo dolů.
(kořeny polynomu) a samozřejmě zda je parabola otevřena nahoru, nebo dolů.
Druhou informaci získáme okamžitě ze zadaného výrazu. Protože je vedoucí koeficient
(![]() ) záporný, je parabola otevřena dolů.
) záporný, je parabola otevřena dolů.
Kořeny dopočítáme pomocí diskriminantu jako by šlo o kvadratickou rovnici:

Graf tedy vypadá takto:
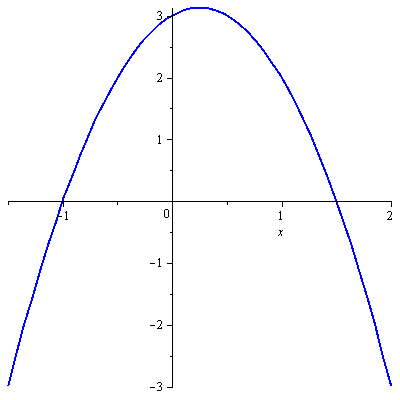
Daný výraz je tedy nezáporný pro
![]() a kladný pro
a kladný pro
![]()
Určete, pro která
![]() je výraz
je výraz
![]() a) kladný, b) nezáporný.
a) kladný, b) nezáporný.
Protože jde o kvadratický polynom, je nejjednodušším způsobem načrtnout si jeho graf - parabolu. Jediné informace, které přitom musí být přesné, jsou průsečíky s osou
![]() (kořeny polynomu) a samozřejmě zda je parabola otevřena nahoru, nebo dolů.
(kořeny polynomu) a samozřejmě zda je parabola otevřena nahoru, nebo dolů.
Druhou informaci získáme okamžitě ze zadaného výrazu. Protože je vedoucí koeficient (
![]() ) kladný, je parabola otevřena nahoru.
) kladný, je parabola otevřena nahoru.
Kořeny dopočítáme pomocí diskriminantu jako by šlo o kvadratickou rovnici:
![]()
Graf tedy vypadá takto:
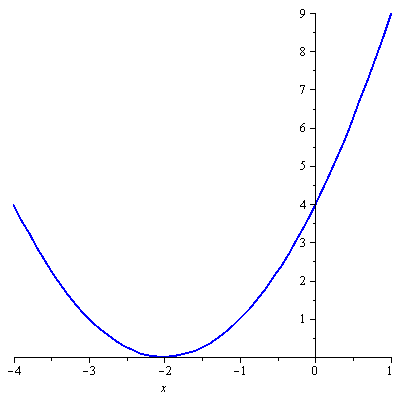
Daný výraz je tedy kladný pro
![]() a nezáporný pro
a nezáporný pro
![]() .
.
Určete, pro která
![]() je výraz
je výraz
![]() a) kladný, b) záporný.
a) kladný, b) záporný.
Protože jde o kvadratický polynom, je nejjednodušším způsobem načrtnout si jeho graf - parabolu. Jediné informace, které přitom musí být přesné, jsou průsečíky s osou
![]() (kořeny polynomu) a samozřejmě zda je parabola otevřena nahoru, nebo dolů.
(kořeny polynomu) a samozřejmě zda je parabola otevřena nahoru, nebo dolů.
Druhou informaci získáme okamžitě ze zadaného výrazu. Protože je vedoucí koeficient (
![]() ) kladný, je parabola otevřena nahoru.
) kladný, je parabola otevřena nahoru.
Kořeny dopočítáme pomocí diskriminantu jako by šlo o kvadratickou rovnici:
![]()
Protože je diskriminant záporný, rovnice nemá žádný reálný kořen a parabola osu
![]() nikde neprotíná. Graf tedy vypadá takto:
nikde neprotíná. Graf tedy vypadá takto:
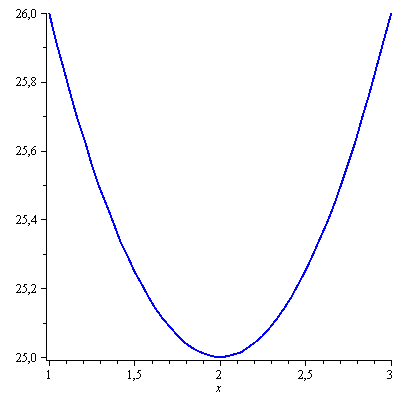
Daný výraz je tedy kladný pro
![]() a nikdy není záporný, tj. můžeme říct, že je záporný pro
a nikdy není záporný, tj. můžeme říct, že je záporný pro
![]() .
.
Určete definiční obor funkce
![]()
Musí platit
![]()
Proto
![]()
Určete definiční obor funkce
![]()
Musí platit
![]()
Nejdříve uvažme
![]() , potom
, potom
![]()
Pro
![]() dostaneme
dostaneme
![]()
proto definiční obor je
![]()
Určete definiční obor funkce
![]()
Musí platit
![]()
Kořeny tohoto kvadratického polynomu jsou
![]() a
a
![]() . Poněvadž koeficient u druhé mocniny je kladný, má graf této kvadratické funkce podobu
. Poněvadž koeficient u druhé mocniny je kladný, má graf této kvadratické funkce podobu
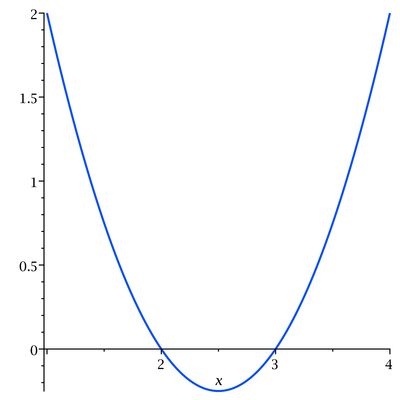
Proto definiční obor funkce je
![]()
Určete definiční obor funkce
![]()
Z logaritmu dostáváme, že
![]() . Dále ve jmenovateli nesmí být nula, tedy v definičním oboru dané funkce nejsou kořeny polynomu
. Dále ve jmenovateli nesmí být nula, tedy v definičním oboru dané funkce nejsou kořeny polynomu
![]() . Snadno určíme, že kořeny jsou
. Snadno určíme, že kořeny jsou
![]() . Tedy
. Tedy
![]()
Určete definiční obor funkce
![]()
Zde určíme nejprve definiční obor každé části dané funkce a poté uděláme jejich průnik. V první části, lomeném výrazu, nesmí být ve jmenovateli nula. Tedy nutně
![]() . V druhé části musí být pod odmocninou nezáporné číslo, odtud
. V druhé části musí být pod odmocninou nezáporné číslo, odtud
![]() . A konečně, z logaritmu dostáváme, že
. A konečně, z logaritmu dostáváme, že
![]() . Celkem
. Celkem
![]()
Určete definiční obor funkce
![]()
Určíme nejprve definiční obor každé části dané funkce a poté uděláme jejich průnik.
V první části musí platit
![]()
Jde o kvadratický polynom jehož grafem je parabola otevřená nahoru (vedoucí koeficient je kladný) a snadno dopočítáme, že jeho kořeny jsou
![]() a
a
![]() . Graf tedy vypadá takto:
. Graf tedy vypadá takto:
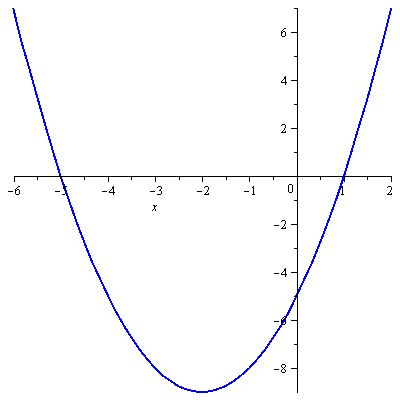
Tedy
![]() .
.
V druhé části nesmí být po odmocninou záporné číslo a zároveň ve jmenovateli není přípustná nula, tj.
![]()
Celkem
![]()
Určete definiční obor funkce
![]()
Nejdříve připomeňme grafy a základní vlastnosti cyklometrických funkcí
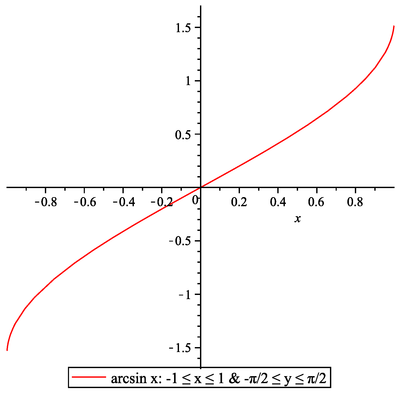
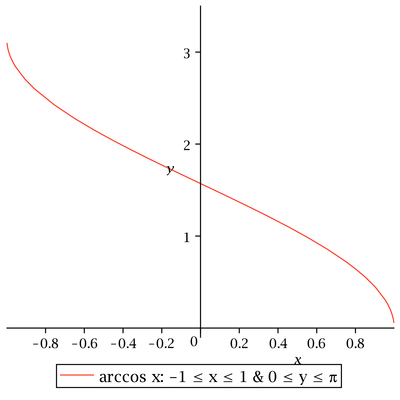
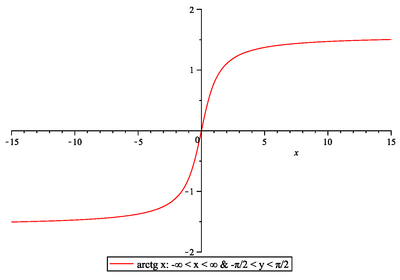
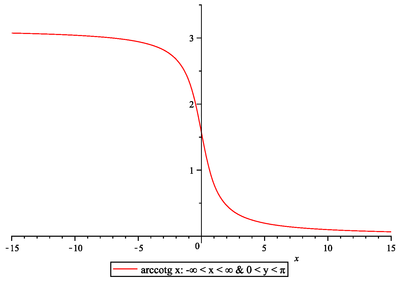
Proto musí platit
|
|
|
|
|
Proto máme definiční obor
![]()
Určete definiční obor funkce
![]()
Určíme nejprve definiční obor každé části dané funkce a poté uděláme jejich průnik.
V první části musí platit
|
|
|
|
|
|
|
|
|
tedy
![]() .
.
V druhé části nesmí být po odmocninou záporné číslo a zároveň ve jmenovateli není přípustná nula. Nulové body jsou přitom
![]() a
a
![]() . Ty rozdělují reálnou osu na tři intervali, na nichž výraz pod odmocninou nabývá vždy stejného znaménka. Dosazením zjistíme jaká (přitom číslo
. Ty rozdělují reálnou osu na tři intervali, na nichž výraz pod odmocninou nabývá vždy stejného znaménka. Dosazením zjistíme jaká (přitom číslo
![]() vůbec neuvažujeme, aby ve jmenovateli nebyla nula):
vůbec neuvažujeme, aby ve jmenovateli nebyla nula):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Odtud dostáváme, že
![]() .
.
Celkem
![]()
Určete definiční obor funkce
![]()
Určíme nejprve definiční obor každé části dané funkce a poté uděláme jejich průnik.
V první části jsou jediná omezení odmocnina a zlomek, tedy
![]() .
.
V druhé části musíme vzít v úvahu jak logaritmus, tak i fakt, že je tento výraz umocněn na záporný exponent, je tedy ve jmenovateli, a proto musí být různý od nuly. Logaritmus je roven nule v jedničce, tj.
![]()
Jako poslední zbývá vyřešit už zmíněný logaritmus, do nějž lze dosazovat pouze kladná čísla, tedy
![]()
Celkem
![]()
Určete definiční obor funkce
![]()
Musí platit
![]()
Graf funkce
![]() má podobu
má podobu
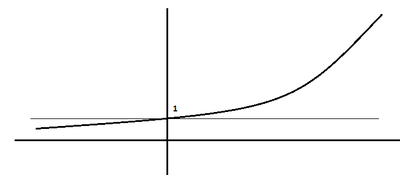
proto je definiční obor
![]()
Určete definiční obor funkce
![]()
Musí platit
![]()
Položme
![]() , potom
, potom
|
|
|
|
|
|
|
|
Proto máme definiční obor
![]()
Určete definiční obor funkce
![]()
Musí platit
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Proto máme definiční obor
![]()
Určete definiční obor funkce
![]()
Musí platit
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Proto máme definiční obor
![]()
Dokažte, že pro
![]() platí
platí
![]()
Položme
![]() a
a
![]() . Potom platí
. Potom platí
![]() a
a
![]() . Musíme ukázat, že
. Musíme ukázat, že
![]() . Proto
. Proto
|
|
|
|
|
|
|
|
|
|
|
Načrtněte graf libovolné nekonstantní funkce ![]() a k něm grafy funkcí:
a k něm grafy funkcí:
![]()
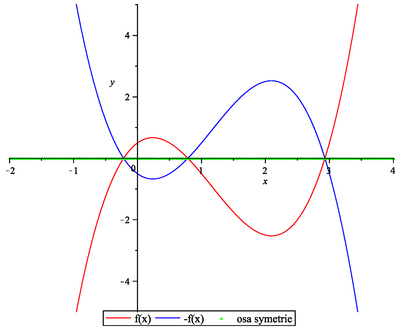
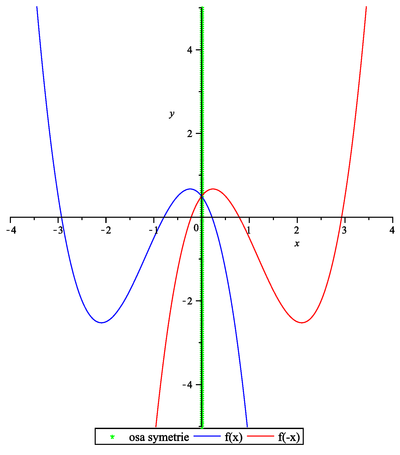
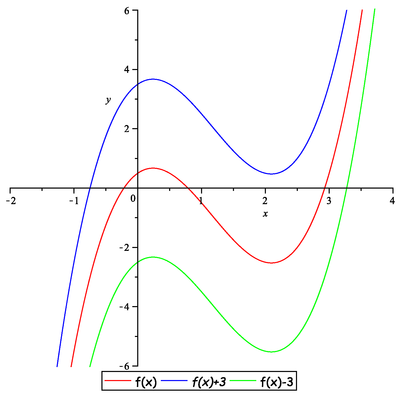
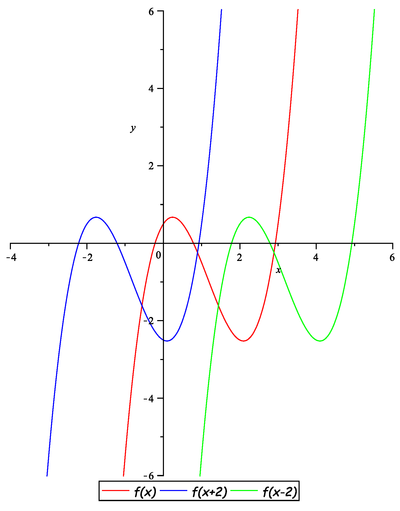
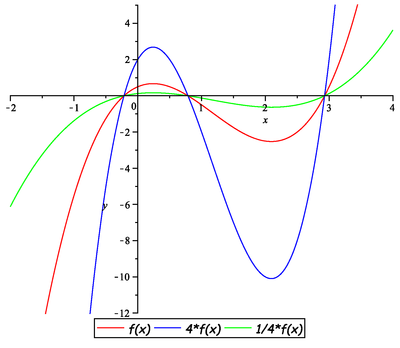
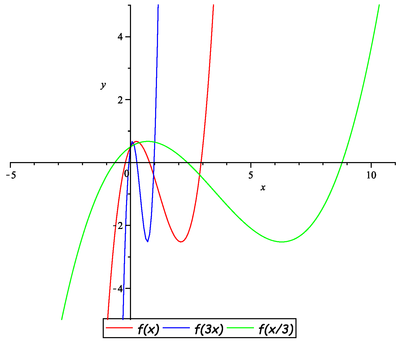
Načrtněte graf funkce
![]()
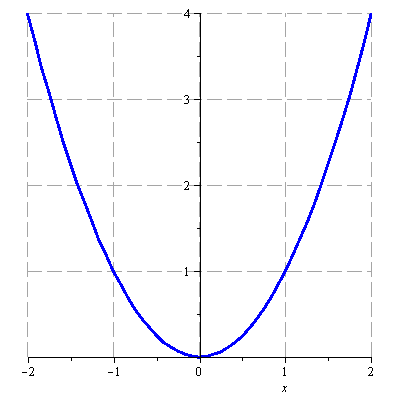
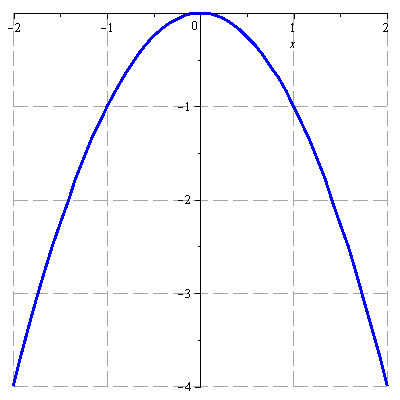
Načrtněte graf funkce
![]()
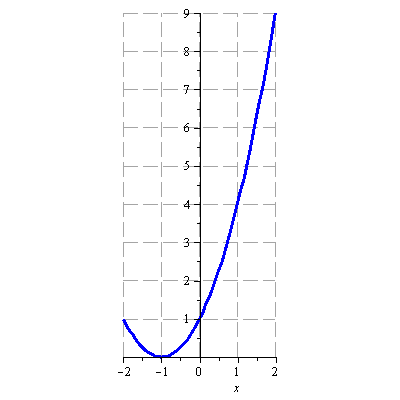
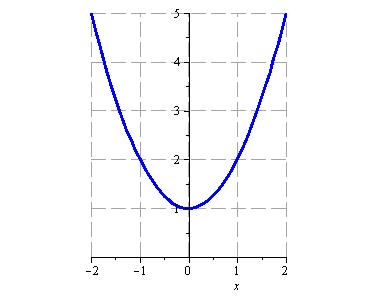
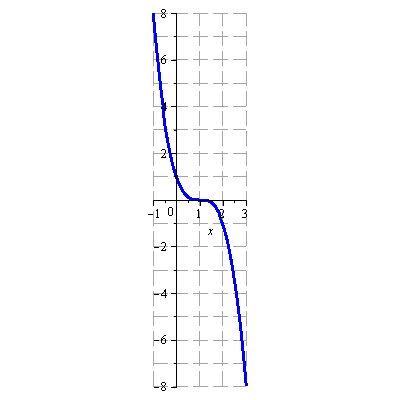
Načrtněte graf funkce
![]()
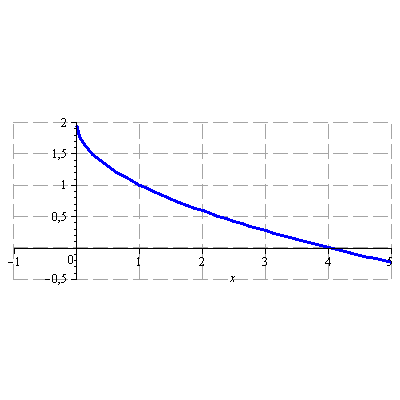
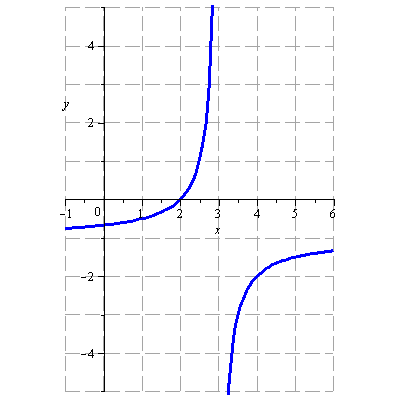
Načrtněte graf funkce
![]()
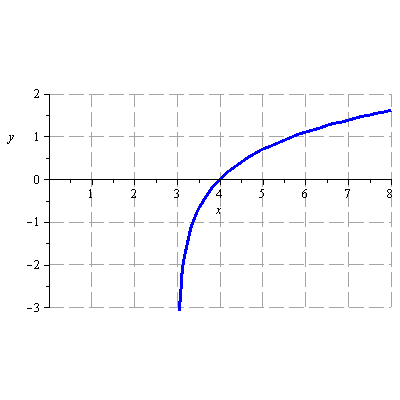
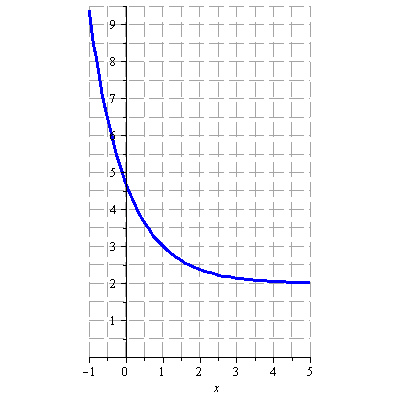
Načrtněte graf funkce
![]()
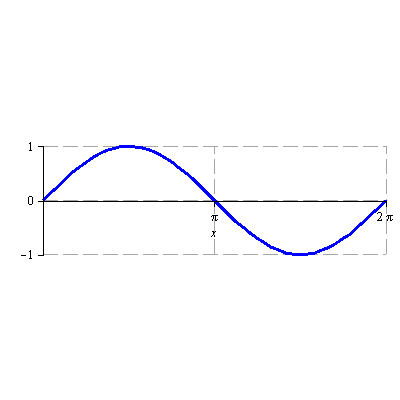
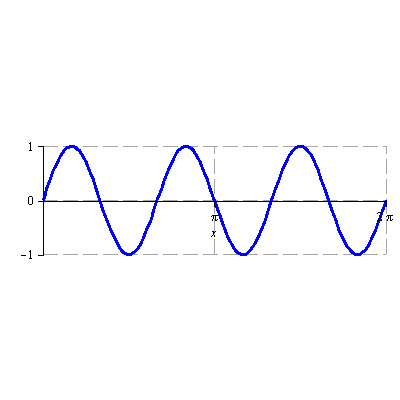
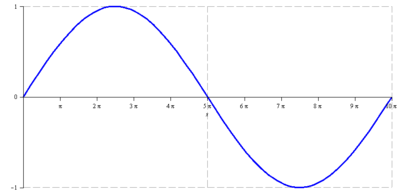
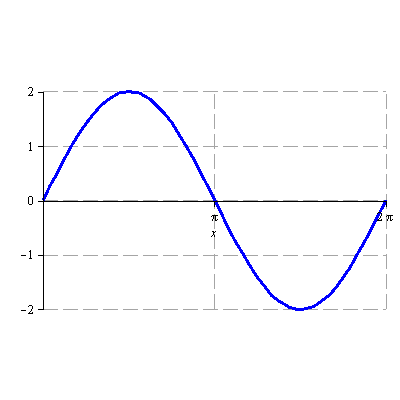
Načrtněte graf funkce
![]()
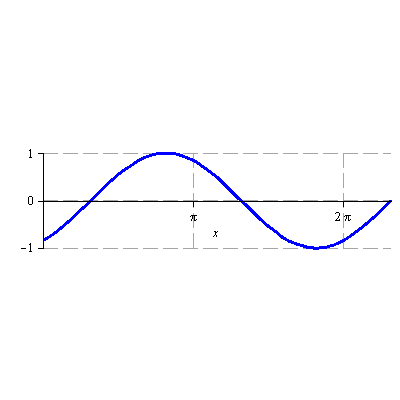
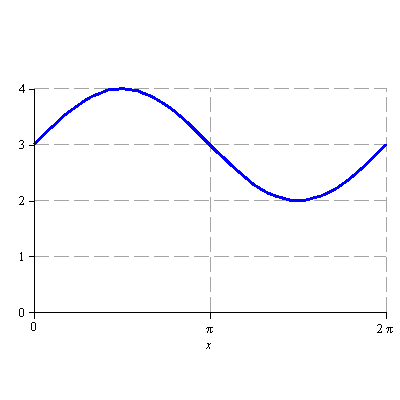
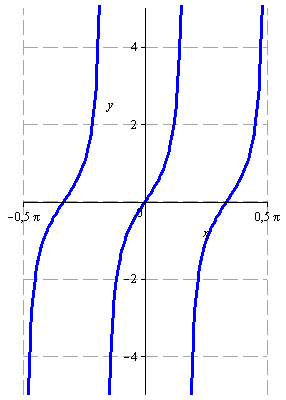
Načrtněte graf funkce
![]()
Nejdříve upravíme zadání do tvaru
|
|
|
|
|
|
|
|
Nyní můžeme využít Příklad 28 a graf funkce
![]() načrtnout díky znalosti grafu funkce
načrtnout díky znalosti grafu funkce
![]() , proto
, proto
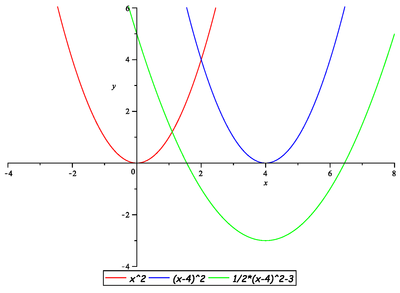
Načrtněte grafy funkcí
![]()
Pomocí řešení Příkladu 28 můžeme ze znalosti grafu funkce
![]() načrtnout graf funkce
načrtnout graf funkce
![]() , tj.
, tj.
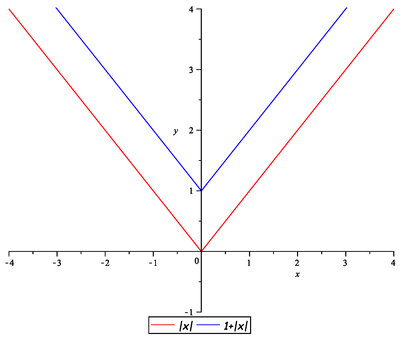
Nyní načrtneme graf funkce
![]() . Nejdříve určíme nulové body jednotlivých absolutních hodnot, tj.
. Nejdříve určíme nulové body jednotlivých absolutních hodnot, tj.
![]() a
a
![]() . Tyto body nám rozdělí reálnou osu na tři subintervaly. Proto
. Tyto body nám rozdělí reálnou osu na tři subintervaly. Proto
|
|
|
|
|
|
|
|
|
Na jednotlivých subintervalech je graf funkce tvořen přímkami, které prochází postupně body
![]() ,
,
![]() ,
,
![]() a
a
![]() , tj.
, tj.
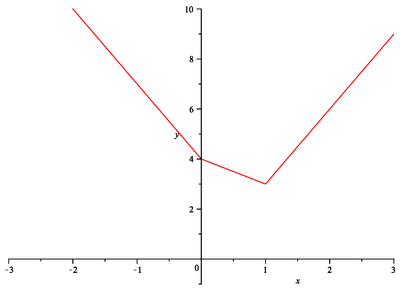
Načrtněte graf funkce
![]()
Je zřejmé, že definiční obor funkce je
![]() . Upravíme zadání funkce, tj.
. Upravíme zadání funkce, tj.
|
|
|
|
|
|
|
|
Ještě určíme průsečík s osou
![]() , tj.
, tj.
|
|
|
|
|
Proto s pomocí Příkladu 28 můžeme načrtnou graf funkce
![]() , tj.
, tj.
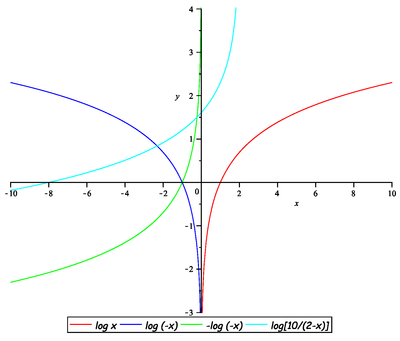
Grafy funkcí na obrázku je potřeba brát pouze ilustrativně (na obrázku je ve skutečnosti přirozený logaritmus
![]() ).
).
Načrtněte graf funkce
![]()
Pro snažší náčrt nejdříve určíme průsečík s osou
![]() , tj.
, tj.
|
|
|
|
|
|
|
|
|
|
|
Osa grafu funkce se posune do
![]() , proto určíme i průsečíky s touto osou, tj.
, proto určíme i průsečíky s touto osou, tj.
|
|
|
|
|
|
|
|
Tedy hledaný graf funkce
![]() má podobu
má podobu
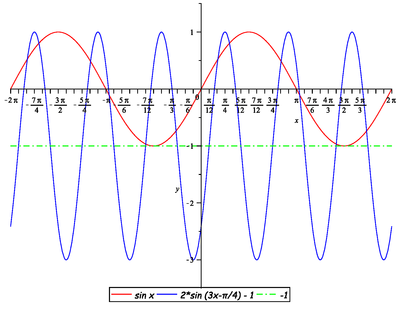
Načrtněte graf funkce
![]()
S pomocí Příkladu 28 dostaneme
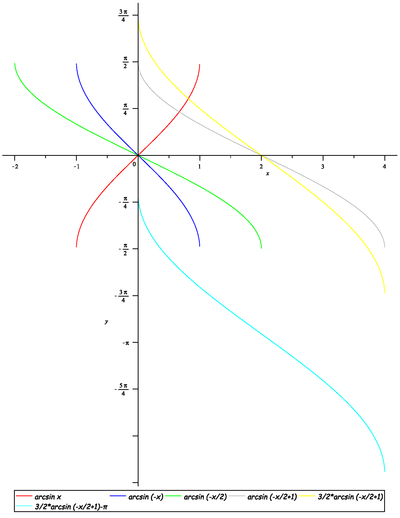
Rozhodněte o paritě funkcí (je daná funkce sudá či lichá?)
-
 ;
Řešení» Zobrazit řešení «
;
Řešení» Zobrazit řešení « ,
,
-
 ;
Řešení» Zobrazit řešení «
;
Řešení» Zobrazit řešení «

-
 ;
Řešení» Zobrazit řešení «
;
Řešení» Zobrazit řešení «


-
 ;
Řešení» Zobrazit řešení «
;
Řešení» Zobrazit řešení «


-
 ;
Řešení» Zobrazit řešení «
;
Řešení» Zobrazit řešení «


-
 .
Řešení» Zobrazit řešení «
.
Řešení» Zobrazit řešení «Nyní si připomene definice hyperbolických funkcí a jejich grafy, tj.
 ,
,
 ,
,
 a
a
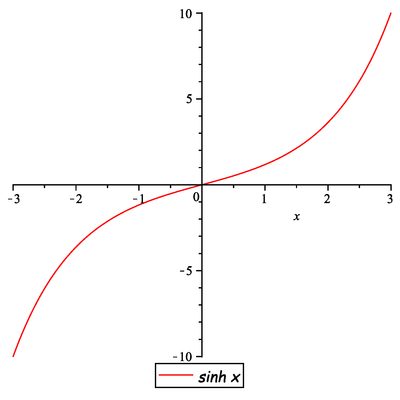
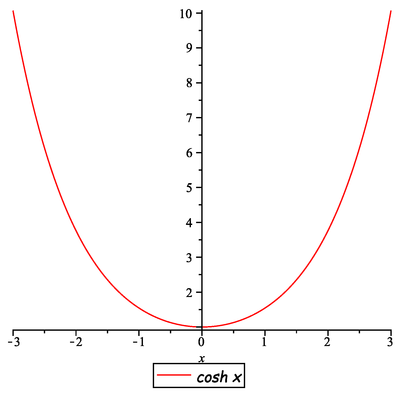
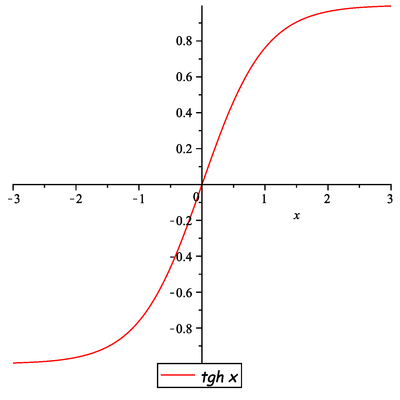
Potom dostaneme



-
Jak se mění parita funkce vzhledem k součtu, rozdílu, součinu a podílu?
Řešení» Zobrazit řešení «
Označme „S“ sudou funkci a „L“ lichou funkci. Pak platí:

jsou sudé funkce,

jsou liché funkce.
Určete inverzní funkci
![]()
Z rovnice
![]()
musíme vyjádřit
![]() , potom přeznačením
, potom přeznačením
![]() dostaneme hledaný předpis pro inverzní funkci. Proto
dostaneme hledaný předpis pro inverzní funkci. Proto
|
|
|
|
|
Určete inverzní funkci
![]()
Z rovnice
![]()
musíme vyjádřit
![]() , potom přeznačením
, potom přeznačením
![]() dostaneme hledaný předpis pro inverzní funkci. Proto
dostaneme hledaný předpis pro inverzní funkci. Proto
|
|
|
|
|
Určete inverzní funkci
![f(x)= \begin{cases} x, & x<1;\\ x^2, &x\in[1,4];\\ 2^x, &x>4. \end{cases} f(x)= \begin{cases} x, & x<1;\\ x^2, &x\in[1,4];\\ 2^x, &x>4. \end{cases}](f.gif)
Přímým výpočtem dostaneme výsledek
![f^{-1}(x)= \begin{cases} x, & x<1;\\ \sqrt{x}, &x\in[1,16];\\ \log_2 x, &x>16. \end{cases} f^{-1}(x)= \begin{cases} x, & x<1;\\ \sqrt{x}, &x\in[1,16];\\ \log_2 x, &x>16. \end{cases}](f.gif)
Určete jednotlivé elementární funkce, z nichž se skládá funkce
![]()
Složky jsou
![]()
Daná funkce je z nich složena takto:
![]()
Určete jednotlivé elementární funkce, z nichž se skládá funkce
![]()
Složky jsou
![]()
Daná funkce je z nich složena takto:
![]()
Určete jednotlivé elementární funkce, z nichž se skládá funkce
![]()
![]() Složky jsou
Složky jsou
![]()
Daná funkce je z nich složena takto:
![]()
![]() Složky jsou
Složky jsou
![]()
Daná funkce je z nich složena takto:
![]()
Vypočtěte
![]() , jestliže
, jestliže
![]()
Musíme za
![]() dosadit takovou hodnotu, aby na levé straně rovnice
dosadit takovou hodnotu, aby na levé straně rovnice
![]() zůstala pouze
„nějaká“
proměnná, zbytek dostaneme pouze přeznačením. Zvolme
zůstala pouze
„nějaká“
proměnná, zbytek dostaneme pouze přeznačením. Zvolme
![]() , potom máme
, potom máme
|
|
|
|
|
Nyní položíme
![]() a dostaneme řešení
a dostaneme řešení
![]()
Vypočtěte
![]() , jestliže
, jestliže
![]() .
.
Využijeme postup z Příkladu 47. Musíme najít vhodnou hodnotu
![]() . Proto musíme vyřešit rovnici
. Proto musíme vyřešit rovnici
![]()
Nyní zvolíme
![]() , potom
, potom
![]()
Pro
![]() jsme našli funkční předpis ve tvaru
jsme našli funkční předpis ve tvaru
![]()
Vyřešte nerovnici
![]()
Nejdříve nerovnost upravíme
|
|
|
|
|
Nulové body absolutních hodnot jsou
![]() a
a
![]() . Tímto se nám rozdělí reálná osa na tři subintervaly, na kterých budeme muset vyřešit nerovnici zvlášť. Proto
. Tímto se nám rozdělí reálná osa na tři subintervaly, na kterých budeme muset vyřešit nerovnici zvlášť. Proto
|
|
|
|
|
|
|
|
Proto řešením je interval
![]() .
.
Dokažte, že aritmetický průměr dvou nezáporných čísel je větší nebo roven jejich průměru geometrickému.
Jinými slovy máme dokázat, že platí
![]()
To plyne z této úvahy
|
|
|
|
|
Pomocí matematické indukce dokažte, že platí Bernoulliova nerovnost
![]()
Nerovnost dokážeme pomocí matematické indukce, proto vezme první možnou hodnotu
![]() , tj.
, tj.
![]() , a ukážeme, že je nerovnost splněna, proto
, a ukážeme, že je nerovnost splněna, proto
![]()
Uděláme indukční krok, proto předpokládejme, že rovnost platí pro nějaké
![]() , tj.
, tj.
![]() . Teď ukážeme, že nerovnost platí i pro
. Teď ukážeme, že nerovnost platí i pro
![]() . Proto
. Proto
|
|
|
|
|
|
|
|
|
|
|
Tedy i pro
![]() je nerovnice splněna. Tím jsme dokázali Bernoulliovu nerovnost.
je nerovnice splněna. Tím jsme dokázali Bernoulliovu nerovnost.
Pomocí matematické indukce dokažte, že pro
![]() platí
platí
![]()
Nejdříve ověříme, že rovnost platí pro
![]() , tj.
, tj.
![]()
Nechť nyní rovnost platí pro libovolné
![]() . Pak pro
. Pak pro
![]() dostaneme
dostaneme
|
|
|
|
|
čímž je identita dokázána.
Pomocí matematické indukce dokažte, že pro
![]() platí
platí
![]()
Nejdříve ověříme, že rovnost platí pro
![]() , tj.
, tj.
![]()
Nechť nyní rovnost platí pro libovolné
![]() . Pak pro
. Pak pro
![]() dostaneme
dostaneme
|
|
|
|
|
čímž je identita dokázána.
Rozklad na parciální zlomky
-
Lomená racionální funkce
 ;
;
-
má-li polynom v čitateli stejný, nebo vyšší stupeň než polynom ve jmenovateli, provedeme dělení polynomů - tím získáme polynom a
ryze lomenou racionální funkci
 (tj.,
(tj.,
 );
);
-
určíme reálné kořeny polynomu
 (pomocí Hornerova schématu, vzorců, vytýkáním či jinými úpravami) a zapíšeme
(pomocí Hornerova schématu, vzorců, vytýkáním či jinými úpravami) a zapíšeme
 jakou součin lineárních polynomů ve tvaru
jakou součin lineárních polynomů ve tvaru
 , kde
, kde
 je reálný kořen, a kvadratických polynomů ve tvaru
je reálný kořen, a kvadratických polynomů ve tvaru
 , které nemají reálné kořeny;
, které nemají reálné kořeny;
-
zapíšeme
 pomocí parciální zlomků s neurčitými koeficienty, přičemž jednoduchému reálnému kořenu
pomocí parciální zlomků s neurčitými koeficienty, přičemž jednoduchému reálnému kořenu
 , tj. členu
, tj. členu
 , odpovídá parciální zlomek ve tvaru
, odpovídá parciální zlomek ve tvaru
jednoduchému komplexnímu kořenu
 , tj. členu
, tj. členu
 , odpovídá parciální zlomek
, odpovídá parciální zlomek
pro
 -násobný reálný kořen
-násobný reálný kořen
 , tj. pro člen
, tj. pro člen
 , odpovídá
, odpovídá
 parciálních zlomků
parciálních zlomků
a pro
 -násobný komplexní kořen
-násobný komplexní kořen
 , tj. pro člen
, tj. pro člen
![[(x-a)^2+b^2]^k [(x-a)^2+b^2]^k](f.gif) , odpovídá
, odpovídá
 parciálních zlomků ve tvaru
parciálních zlomků ve tvaru
![\dfrac{B_1x+C_1}{(x-a)^2+b^2}+\dfrac{B_2x+C_2}{[(x-a)^2+b^2]^2}+\cdots+\dfrac{B_kx+C_k}{[(x-a)^2+b^2]^k}; \dfrac{B_1x+C_1}{(x-a)^2+b^2}+\dfrac{B_2x+C_2}{[(x-a)^2+b^2]^2}+\cdots+\dfrac{B_kx+C_k}{[(x-a)^2+b^2]^k};](f.gif)
- metodou neurčitých koeficientů (příp. s pomocí dosazení některých kořenů) určíme všechny neznámé koeficienty v čitatelích parciálních zlomků.
Rozložte na parciální zlomky
![]()
Nejdříve musíme rozložit jmenovatele na součin, tj. učit kořeny. K tomu můžeme využít tzv. Hornerovo schéma (viz později) nebo některou z elementárních úprav, proto
![]()
Proto rozklad na parciální zlomky musí vypadat takto
![]()
Pro další výpočet musíme obě strany rovnice vynásobit jmenovatelem původního zlomku, proto
|
|
|
|
|
|
Pro určení jednotlivých koeficientů lze využít dosazení jednotlivých kořenů (zde pouze
![]() ), ovšem takovým způsobem dostaneme všechny hledané koeficienty pouze v případě jednoduchých reálných kořenů. Druhou možností je tzv. metoda neurčitých koeficientů, kdy porovnáváme koeficienty u jednotlivých mocnin
), ovšem takovým způsobem dostaneme všechny hledané koeficienty pouze v případě jednoduchých reálných kořenů. Druhou možností je tzv. metoda neurčitých koeficientů, kdy porovnáváme koeficienty u jednotlivých mocnin
![]() , tj.
, tj.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tím jsme obdrželi soustavu tří rovnic o třech neznámých, kterou lze vyřešit přímo (metodami známých ze střední školy nebo pomocí matic). Řešením jsou hodnoty
![]() ,
,
![]() a
a
![]() . Tedy hledaný rozklad je tvaru
. Tedy hledaný rozklad je tvaru
![]()
Při hledání je možné použít i kombinaci obou popsaných metod - část koeficientů získat dosazením kořenů a zbytek metodou neurčitých koeficientů, kde bude nutné již vyřešit nižší počet rovnic.
Rozložte na parciální zlomky
![]()
Rozložením jmenovatele (buď se znalostí vhodného vzorce nebo z faktu, že
![]() je kořen tohoto polynomu, a dále pomoci dělení dvou polynomů) obdržíme
je kořen tohoto polynomu, a dále pomoci dělení dvou polynomů) obdržíme
![]() . Proto rozklad musí vypadat takto
. Proto rozklad musí vypadat takto
![]()
což vede k rovnici
![]()
Pomocí metody neurčitých koeficientů dostaneme soustavu
|
|
|
|
|
|
|
|
|
|
|
|
jejímž řešením je trojice
![]() ,
,
![]() a
a
![]() . Proto máme
. Proto máme
![]()
Rozložte na parciální zlomky
![]()
Jmenovatel je již ve tvaru požadovaného součinu, proto rozklad musí vypadat takto
![]()
z čehož obdržíme rovnici
![]()
Tedy metodou neurčitých koeficientů dostaneme soustavu
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jejímž řešením je čtveřice
![]() ,
,
![]() ,
,
![]() a
a
![]() . Proto hledaný rozklad je tvaru
. Proto hledaný rozklad je tvaru
![]()
Rozložte na parciální zlomky
![]()
Jmenovatel upravíme do tvaru
![]()
proto parciální zlomky musí být ve tvaru
![]()
Úpravou dostaneme rovnici
![]()
což nám metodou neurčitých koeficientů dá soustavu rovnic
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Řešením soustavy je čtveřice
![]() ,
,
![]() ,
,
![]() a
a
![]() , proto hledaný rozklad je tvaru
, proto hledaný rozklad je tvaru
![]()
Rozložte na parciální zlomky
![]()
Poněvadž jsou stupně obou polynomů (alespoň) stejné, musíme nejdříve zadaný podíl upravit tak, abychom dostali ryzí racionální lomenou funkci, tj.
|
|
|
|
|
|
|
|
Nyní musíme rozložit jmenovatele
![]() na součin. Má-li polynom celočíselné kořeny, musí to být dělitelé absolutního členu. Má-li polynom racionální kořen (tj. ve tvaru zlomku), je čitatel zlomku tvořen dělitelem absolutního člene polynomu a jmenovatel tohoto kořene je dělitelem koeficientu u nejvyšší mocniny polynomu. Tuto skutečnost využijeme při aplikování Hornerova schématu, kde postupujeme takto:
na součin. Má-li polynom celočíselné kořeny, musí to být dělitelé absolutního členu. Má-li polynom racionální kořen (tj. ve tvaru zlomku), je čitatel zlomku tvořen dělitelem absolutního člene polynomu a jmenovatel tohoto kořene je dělitelem koeficientu u nejvyšší mocniny polynomu. Tuto skutečnost využijeme při aplikování Hornerova schématu, kde postupujeme takto:
-
Nejprve sepíšeme do tabulky koeficienty studovaného polynomu. (Přitom nesmíme zapomenout na možné nulové koeficienty.)








-
Tabulku rozšíříme o jeden sloupec, do něhož budeme psát kandidáty na kořeny.






-
První (vedoucí) koeficient polynomu sepíšeme do řádku s kandidátem na kořen.

![\textcolor[rgb]{1.00,0.00,0.00}{1} \textcolor[rgb]{1.00,0.00,0.00}{1}](f.gif)




![\textcolor[rgb]{1.00,0.00,0.00}{1} \textcolor[rgb]{1.00,0.00,0.00}{1}](f.gif)
-
Nyní nastupuje hlavní část - doplnění zbylých polí druhého řádku tabulky.


![\textcolor[rgb]{0.00,1.00,0.00}{0} \textcolor[rgb]{0.00,1.00,0.00}{0}](f.gif)


![\textcolor[rgb]{0.00,0.00,1.00}{2} \textcolor[rgb]{0.00,0.00,1.00}{2}](f.gif)
![\textcolor[rgb]{1.00,0.00,0.00}{1} \textcolor[rgb]{1.00,0.00,0.00}{1}](f.gif)
![\textcolor[rgb]{0.00,0.00,1.00}{2} \cdot \textcolor[rgb]{1.00,0.00,0.00}{1}+ \textcolor[rgb]{0.00,1.00,0.00}{0} = 2 \textcolor[rgb]{0.00,0.00,1.00}{2} \cdot \textcolor[rgb]{1.00,0.00,0.00}{1}+ \textcolor[rgb]{0.00,1.00,0.00}{0} = 2](f.gif)
-
Tím dostaneme tabulku





![\textcolor[rgb]{0.00,0.00,1.00}{2} \textcolor[rgb]{0.00,0.00,1.00}{2}](f.gif)


![\textcolor[rgb]{0.00,0.00,1.00}{2} \cdot 2 + 1 = 5 \textcolor[rgb]{0.00,0.00,1.00}{2} \cdot 2 + 1 = 5](f.gif)
![\textcolor[rgb]{0.00,0.00,1.00}{2} \cdot 5 - 2 = 8 \textcolor[rgb]{0.00,0.00,1.00}{2} \cdot 5 - 2 = 8](f.gif)
-
Protože poslední číslo v druhém řádku je různé od nuly, číslo
 není kořenem studovaného polynomu
není kořenem studovaného polynomu
 . (Poznamenejme, že tato pozice obsahuje funkční hodnotu studovaného polynomu v testovaném čísle.)
. (Poznamenejme, že tato pozice obsahuje funkční hodnotu studovaného polynomu v testovaném čísle.)
-
Druhý řádek tabulky vymažeme (v zápise na papír ho škrtáme a rozšíříme tabulku o volný řádek) a otestujeme v něm dalšího kandidáta na kořen.










-
Poslední pozice druhého řádku je nulová, což znamená, že studovaný polynom nabývá v čísle
 hodnoty
hodnoty
 . Číslo
. Číslo
 je tedy kořenem polynomu
je tedy kořenem polynomu
 . Ostatní čísla (tj. mimo prvního a posledního) v druhém řádku tabulky navíc udávají koeficienty polynomu vzniklého vydělením studovaného polynomu kořenovým činitelem právě nalezeného kořene.
. Ostatní čísla (tj. mimo prvního a posledního) v druhém řádku tabulky navíc udávají koeficienty polynomu vzniklého vydělením studovaného polynomu kořenovým činitelem právě nalezeného kořene.















-
Shrňme si předchozí postup do jediné tabulky.










![\textcolor[rgb]{0.00,0.00,1.00}{2} \textcolor[rgb]{0.00,0.00,1.00}{2}](f.gif)
![\textcolor[rgb]{1.00,0.00,0.00}{1} \textcolor[rgb]{1.00,0.00,0.00}{1}](f.gif)
![\textcolor[rgb]{0.00,0.00,1.00}{2} \cdot \textcolor[rgb]{1.00,0.00,0.00}{1}+ \textcolor[rgb]{0.00,1.00,0.00}{0} = 2 \textcolor[rgb]{0.00,0.00,1.00}{2} \cdot \textcolor[rgb]{1.00,0.00,0.00}{1}+ \textcolor[rgb]{0.00,1.00,0.00}{0} = 2](f.gif)












Tímto postupem jsme dostali
![]() . Proto rozklad musí být
. Proto rozklad musí být
![]()
z čehož dostaneme rovnici
![]()
neboli
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Řešením této soustavy je čtveřice
![]() ,
,
![]() a
a
![]() , proto hledaný rozklad je ve tvaru
, proto hledaný rozklad je ve tvaru
![]()
Rozložte na parciální zlomky
![]()
Nejdříve upravíme jmenovatele, tj.
![]() . S využitím substituce
. S využitím substituce
![]() dostaneme kvadratickou rovnici
dostaneme kvadratickou rovnici
![]() s řešeními
s řešeními
![]() a
a
![]() . Proto jmenovatele můžeme rozložit do tvaru
. Proto jmenovatele můžeme rozložit do tvaru
![]() . Hledaný rozklad tedy musí být ve tvaru
. Hledaný rozklad tedy musí být ve tvaru
![]()
z čehož dostaneme rovnici
|
|
|
|
|
Odtud metodou neurčitých koeficientů dostaneme soustavu rovnic
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a její řešení
![]() ,
,
![]() ,
,
![]() ,
,
![]() a
a
![]() . Tím jsme získali rozklad na parciální zlomky
. Tím jsme získali rozklad na parciální zlomky
![]()
Rozložte na parciální zlomky
![]()
Upravíme jmenovatele do tvaru
![]() a s pomocí Hornerova schématu
a s pomocí Hornerova schématu
|
|
|
|
|
|
|
|
|
|
|
|
zjistíme, že
![]() je také kořenem a další rozklad je ve tvaru
je také kořenem a další rozklad je ve tvaru
![]() , proto rozklad bude mít podobu
, proto rozklad bude mít podobu
![]()
Odtud dostaneme rovnici
|
|
|
|
|
Metodou neurčitých koeficientů získáme soustavu
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s řešeními
![]() ,
,
![]() ,
,
![]() a
a
![]() . Proto hledaný rozklad je ve tvaru
. Proto hledaný rozklad je ve tvaru

Rozložte na parciální zlomky
![]()
Nejdříve získáme ryzí racionální funkci, tj.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Poněvadž platí
![]() , bude rozklad ve tvaru
, bude rozklad ve tvaru
![]()
což vede k rovnici
![]()
S využitím metody neurčitých koeficientů obdržíme soustavu
|
|
|
|
|
|
|
|
s řešením
![]() a
a
![]() . Řešením je tedy rozklad
. Řešením je tedy rozklad
![]()
Rozložte na parciální zlomky
![]()
Úpravou jmenovatele obdržíme
![]() , proto musí být rozklad ve tvaru
, proto musí být rozklad ve tvaru
![]()
což vede na rovnici
![]()
Pomocí metody neurčitých koeficientů obdržíme soustavu
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a její řešení
![]() ,
,
![]() ,
,
![]() a
a
![]() . Proto hledaný rozklad je ve tvaru
. Proto hledaný rozklad je ve tvaru
![]()
Rozložte na parciální zlomky
![]()
Upravíme jmenovatele do tvaru součinu, tj.
![]() , proto bude rozklad mít podobu
, proto bude rozklad mít podobu
![]()
Odtud dostaneme rovnici
![]()
což nás metodou neurčitých koeficientů přivede k soustavě
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s řešením
![]() ,
,
![]() ,
,
![]() a
a
![]() . Proto hledaný rozklad je ve tvaru
. Proto hledaný rozklad je ve tvaru
![]()
Rozložte na parciální zlomky
![]()
S pomocí Hornerova schématu dostaneme
|
|
|
|
|
|
|
|
|
|
|
|
proto platí
![]() . Tedy rozklad bude ve tvaru
. Tedy rozklad bude ve tvaru
![]()
což vede k rovnici
![]()
Metodou neurčitých koeficientů dostaneme soustavu

s řešením
![]() ,
,
![]() a
a
![]() . Hledaný rozklad je tedy tvaru
. Hledaný rozklad je tedy tvaru
![]()
Rozložte na parciální zlomky
![]()
Upravíme jmenovatele do tvaru
![]() , proto rozklad bude ve tvaru
, proto rozklad bude ve tvaru
![]()
Odtud dostaneme rovnici ve tvaru
![]()
Metodou neurčitých koeficientů dostaneme soustavu
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s řešením
![]() ,
,
![]() ,
,
![]() a
a
![]() . Proto hledaný rozklad je ve tvaru
. Proto hledaný rozklad je ve tvaru
![]()
Rozložte na parciální zlomky
![]()
Jmenovatele již nelze nijak rozložit, proto rozklad musí být v tomto tvaru
![]()
což vede na rovnici
![]()
Metodou neurčitých koeficientů dostaneme soustavu rovnic
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s řešením
![]() ,
,
![]() ,
,
![]() a
a
![]() . Proto hledaný rozklad je tvaru
. Proto hledaný rozklad je tvaru
![]()
Rozložte na parciální zlomky
![]()
Nejdříve upravíme jmenovatele do tvaru
![]()
Proto bude rozklad ve tvaru
![]()
z čehož obdržíme rovnici
|
|
|
|
|
Metodou neurčitých koeficientů dostaneme soustavu
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a řešení
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() a
a
![]() . Tedy hledaný rozklad je ve tvaru
. Tedy hledaný rozklad je ve tvaru
![]()
Rozložte na parciální zlomky
![]()
Pomocí vytýkání upravíme jmenovatele do tvaru
![]()
S využitím Hornerova schématu
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
můžeme psát
![]()
Proto rozklad bude ve tvaru
|
|
|
|
|
což vede na rovnici
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pomocí metody neurčitých koeficientů dostaneme soustavu
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s řešením
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() a
a
![]() . Proto hledaný rozklad je ve tvaru
. Proto hledaný rozklad je ve tvaru
|
|
|
|
|
Tisková verze
ÚMS, Přírodovědecká fakulta, Masarykova univerzita |
Návrat na úvodní stránku webu, přístupnost |
| Servisní středisko pro e-learning na MU
| Fakulta informatiky Masarykovy univerzity, 2012
Technické řešení této výukové pomůcky je spolufinancováno Evropským sociálním fondem a státním rozpočtem České republiky.


