Základní pojmy 

V našem kurzu se budeme zabývat určováním průniků roviny a mnohostěnu. Neprázdný průnik mnohostěnu a roviny budeme nazývat rovinným řezem mnohostěnu. Místo rovinný řez mnohostěnu budeme užívat též stručnější vyjádření – řez mnohostěnu a uvažovanou rovinu budeme nazývat rovinou řezu.

Dále budeme pracovat pouze s konvexními mnohostěny. Průnikem konvexního mnohostěnu s rovinou (také konvexní množinou bodů) je konvexní množina bodů. Je tedy zřejmé, že platí:
Řezem konvexního mnohostěnu je neprázdná konvexní množina bodů v rovině řezu.

Podle polohy mnohostěnu a roviny řezu mohou nastat  možnosti:

  1. Rovina řezu obsahuje aspoň jeden vnitřní bod (konvexního) mnohostěnu.
  2. Rovina řezu neobsahuje vnitřní bod mnohostěnu.

I. Rovina řezu obsahuje aspoň jeden vnitřní bod konvexního mnohostěnu 

V obrázku 1 je zobrazen jehlan VABCD a jeho řez rovinou MNP. Je zřejmé, že rovina MNP obsahuje vnitřní body jehlanu VABCD; např. každý bod patřící úsečce PM – s výjimkou bodů P, M – je vnitřním bodem jehlanu. Řezem jehlanu VABCD je čtyřúhelník MNPQ. Je zřejmé, že platí:

Obsahuje-li rovina řezu alespoň jeden vnitřní bod konvexního mnohostěnu, je řezem konvexní mnohoúhelník. Jeho vrcholy jsou průsečíky roviny řezu s hranami mnohostěnu a jeho strany jsou průniky (neprázdné) stěn mnohostěnu s rovinou řezu.

Obr. 1
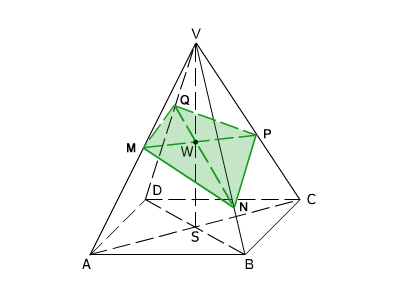
Obr.1

Je zřejmé, že vrchol řezu je současně průsečík přímky, která obsahuje proťatou hranu, s rovinou řezu a že strana řezu je částí průsečnice roviny řezu s rovinou stěny mnohostěnu, v níž tato strana leží.

Při konstrukcích rovinných řezů mnohostěnů tedy opakovaně řešíme dvě základní úlohy:

  • určení průsečíku přímky s rovinou
  • určení průsečnice dvou rovin.

Připomeňme si

Máme-li určit průsečík P přímky p s rovinou ρ, postupujeme zpravidla takto: Přímkou p proložíme vhodnou pomocnou rovinu a určíme její průsečnici r s danou rovinou ρ. Průsečík P dané přímky p s rovinou ρ je průsečík přímek p a r (pokud existuje).Obr.2.

Obr. 2
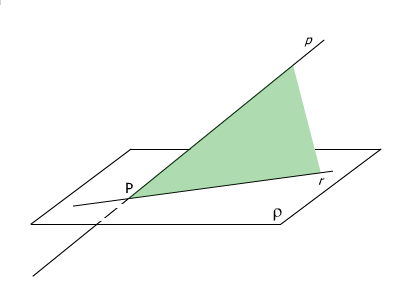
Obr.2

Pro určení průsečnice dvou rovin α, β je třeba určit dva jejich různé společné body. Přitom společný bod dvou rovin můžeme nalézt např. tak, že určíme průsečík vhodně zvolené přímky jedné z rovin s druhou rovinou. Ve 3. obrázku je přímka a ⊂ α a bod X je průsečík přímky a s rovinou β. Podobně je přímka b ⊂ β a bod Y je průsečík přímky b s rovinou α. Body X, Y určují průsečnici r rovin α, β.

Obr. 3
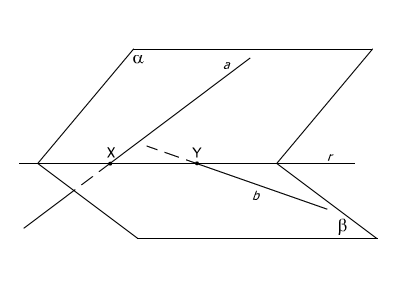
Obr.3

II. Rovina řezu neobsahuje žádný vnitřní bod konvexního mnohostěnu 

Neobsahuje-li rovina řezu žádný vnitřní bod konvexního mnohostěnu, může být průnikem této roviny a konvexního mnohostěnu:

  • konvexní mnohoúhelník – některá stěna konvexního mnohostěnu (obr.4),

Obr. 4
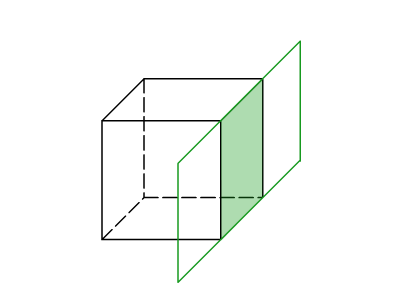
Obr.4

  • úsečka – některá hrana konvexního mnohostěnu (obr.5),

Obr. 5
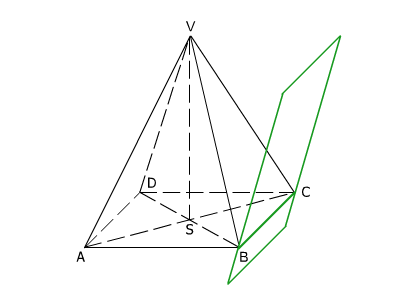
Obr.5

  • bod – (přesněji jednobodová množina) – některý vrchol konvexního mnohostěnu (obr.6),

Obr. 6
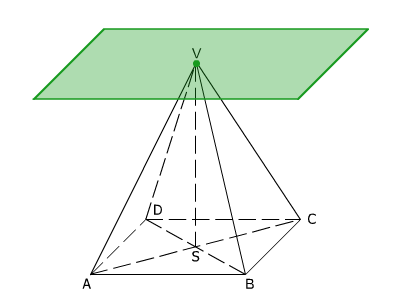
Obr.6

  • prázdná množina – v tomto případě nejde o řez.

Obr. 7
Obr.7
Logo Pedagogické fakulty
| Technická spolupráce:
| Servisní středisko pro e-learning na MU, 2008
| Stránky střediska na Elportále