Důkazy
Obsah oddílu
Typy matematických vět a základní metody jejich důkazů
Stručný přehled teorie
Matematika nepřipouští plané řeči o pojmech, jejichž smysl není jasně a jednoznačně stanoven.
Každý matematický pojem musí být přesně definován.




Metodika
Všechny matematické informace, se kterými se dosud studenti setkali na základní škole nebo v prvních měsících studia na gymnáziu, brali jako samozřejmost. Nepochybovali o ničem, co slyšeli z úst svého vyučujícího matematiky. Na otázku „Jaký je součet vnitřních úhlů v trojúhelníku?“ odpověděli „180°“. Na otázku „Kolik kolmic lze vést daným bodem k dané přímce?“ odpověděli „jednu“ nebo „právě jednu“. … Nyní nastal čas, aby učitel poprvé vyvolal u studentů pochybnost o věcech, které dosud považovali za dané a jednoznačné, aby je přinutil přemýšlet novým způsobem, aby v nich vyvolal zvědavost a touhu objevovat nové věci za tajemnými dveřmi, které se před nimi v matematice pootevírají. Stačí k tomu vyslovit jednoduchou a prostou námitkou „Určitě? Nemůže to být třeba 181°? Proč je to právě 180°?“, nebo „Jsi si jist, že jen jedna kolmice? Co když nakreslím dvě nebo tři těsně vedle sebe? Půjde to? Budou to všechno kolmice? Proč myslíš, že ne? Zkusíš to dokázat?“ Je docela možné, že se mezi studenty najde některý s mimořádným matematickým talentem, komu se (vzhledem k relativní jednoduchosti problému) podaří přiblížit se úvahou ke správnému důkazu.
Téma (s výjimkou matematické indukce, která se zpravidla probírá odděleně – až u kombinatoriky a posloupností) by mělo být zařazeno bezprostředně po probrání Výrokové logiky v prvním ročníku čtyřletého gymnázia. V žádném případě by nemělo mít podobu přednášky a nemělo by se zařazovat až do předmaturitního období, jak se doporučuje v kapitole „Logická stavba matematiky“ na Matematika SŠ.realisticky.cz. Je sice pravda, že téma je velmi náročné a patří nepochybně k nejobtížnějším pasážím matematiky, s jakými se studenti dosud setkali. Ale zařazení těsně po Výrokové logice zaručí nejlepší pochopení všech užívaných jevů a souvislostí a zároveň umožní důkladné procvičení a prohloubení znalostí z oblasti formální logiky. Vzhledem k tomu, že celou gymnaziální matematikou, všemi probíranými tématy, od prvního až po maturitní ročník se jako červená nit táhne spousta důkazových úloh, nelze rozhodně s probráním principů důkazů matematických vět otálet a připustit, aby studenti předmaturitních ročníků při řešení důkazových úloh nevěděli nic o principech důkazů. Naopak, studenti musí umět zvolit vhodnou důkazovou metodu a rozumět každému jejímu kroku.
Místo přednášky by měl učitel využít materiálů zpracovaných v teorii k tomuto tématu. Tyto materiály by měl dát studentům k dispozici a projít s nimi společně úvod až po typy matematických vět a princip první důkazové metody.
Každý typ matematické věty a každý způsob jejího důkazu by pak měl učitel studentům důkladně vysvětlit za pomoci obecného principu ze zpracovaných teoretických materiálů, které studenti dostali, a demonstrovat (samozřejmě za vydatné pomoci studentů) důkaz na jednom, dvou či několika konkrétních zadáních.
Sbírky úloh ze středoškolské matematiky jsou plné úloh důkazových. Učitel by si měl dát práci, vyhledat třeba 15 – 20 takových zadání (případně zvolit počet podle vlastního uvážení), soustředit je do jednoho materiálu, dát jej studentům k dispozici k procvičení a vyučovací hodiny potom organizovat tak, aby si studenti pod jeho dohledem některé důkazy vyzkoušeli, případně aby v rámci konzultačních částí hodin zodpověděl dotazy.

Úloha 7.1.1
Dokažte, že v každém trojúhelníku je součet vnitřních úhlů roven 180°. (Euklidovská geometrie)
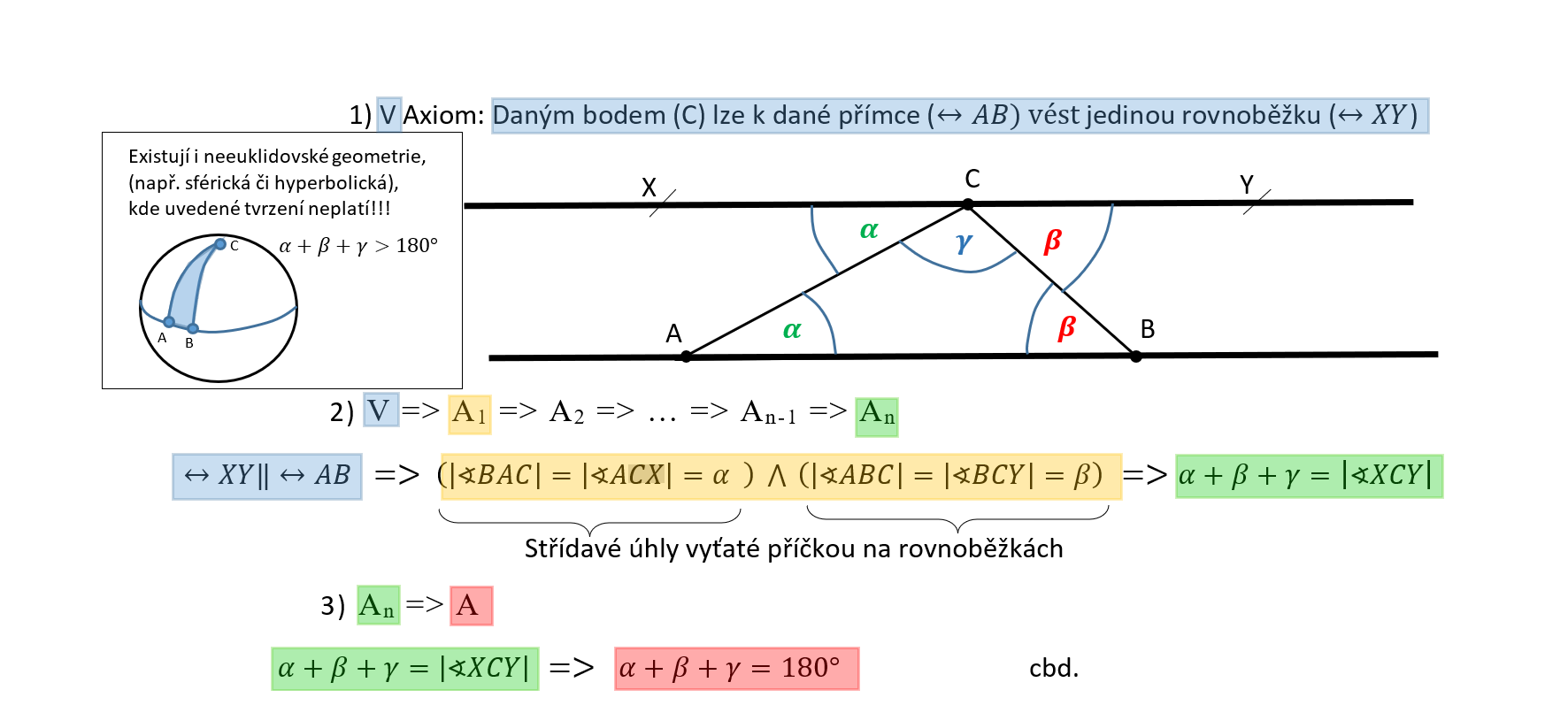
Úloha 7.1.2
Dokažte, že součet libovolných pěti po sobě následujících přirozených čísel je dělitelný pěti.

Úloha 7.1.3
Dokažte, že platí: $\sqrt{13+\sqrt{12}} \le 1 + \sqrt{13-\sqrt{12}}$.
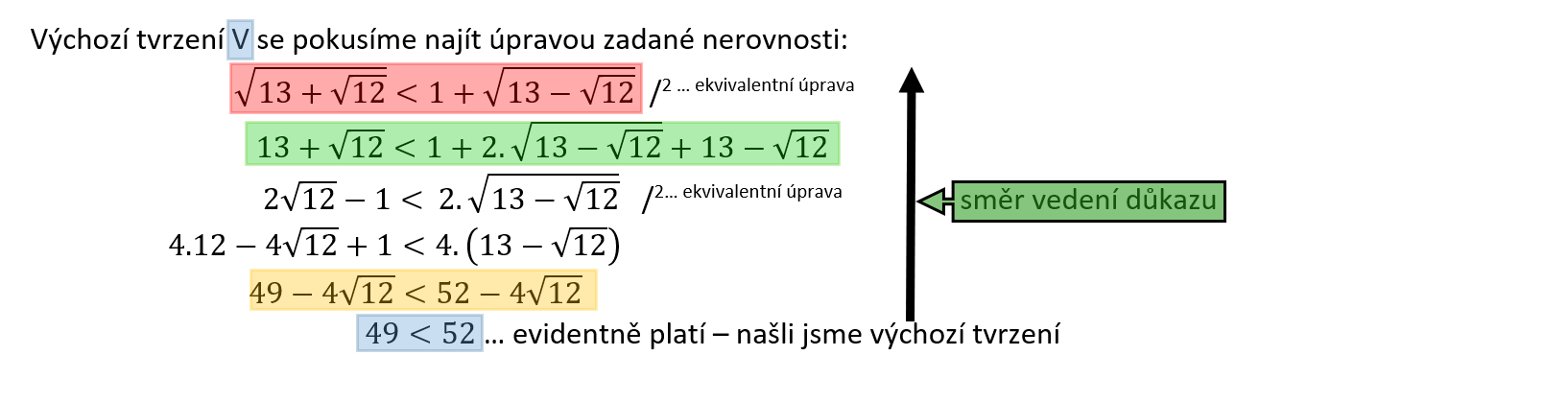
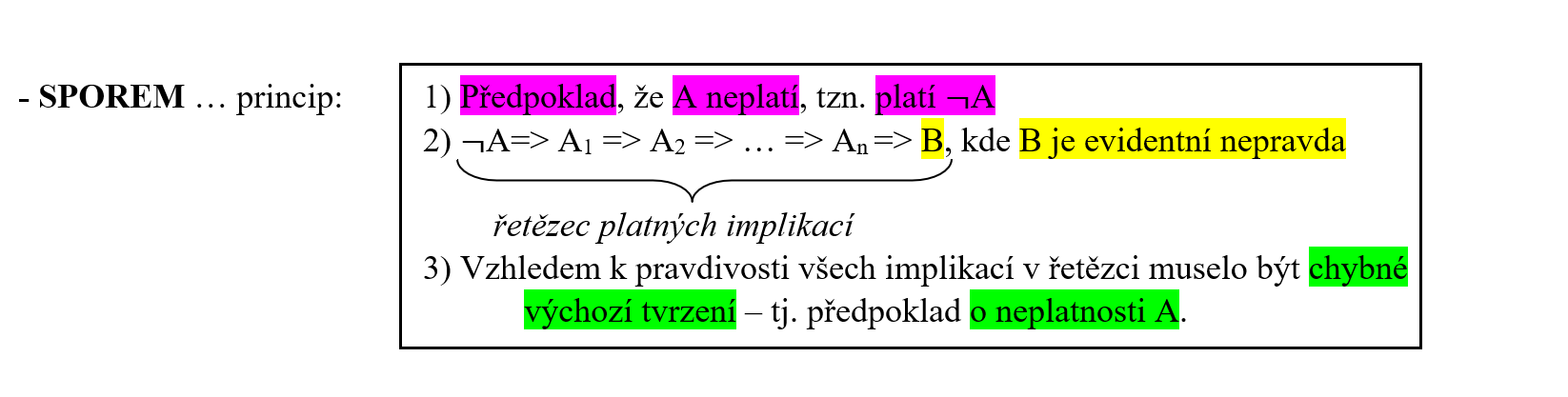
Úloha 7.1.4

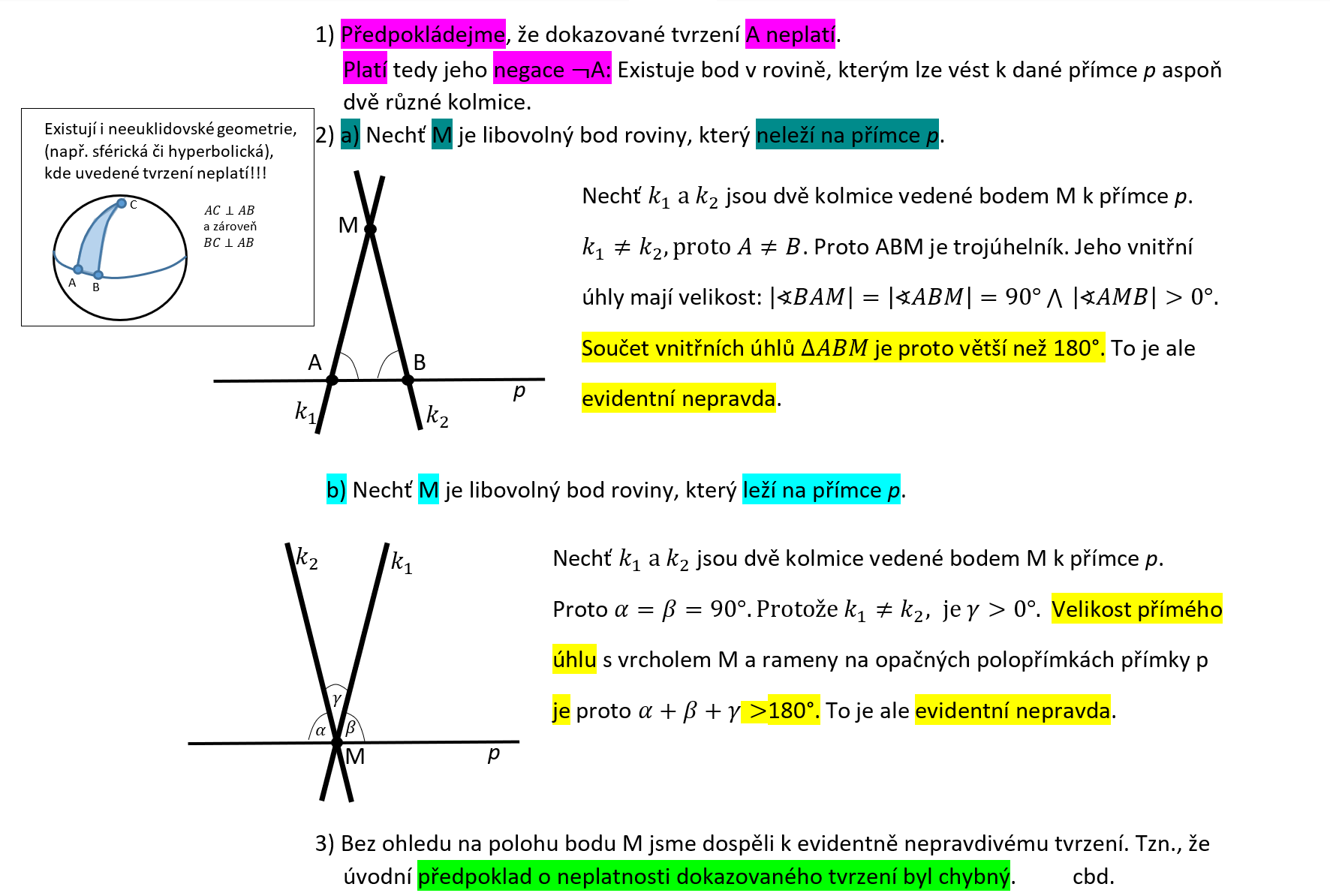
Úloha 7.1.5
Dokažte, že prvočísel je nekonečně mnoho. (Pozn. Jde o nádhernou historickou úlohu, kterou vyřešil už tři století př. n. l. Eukleidés z Alexandrie.)

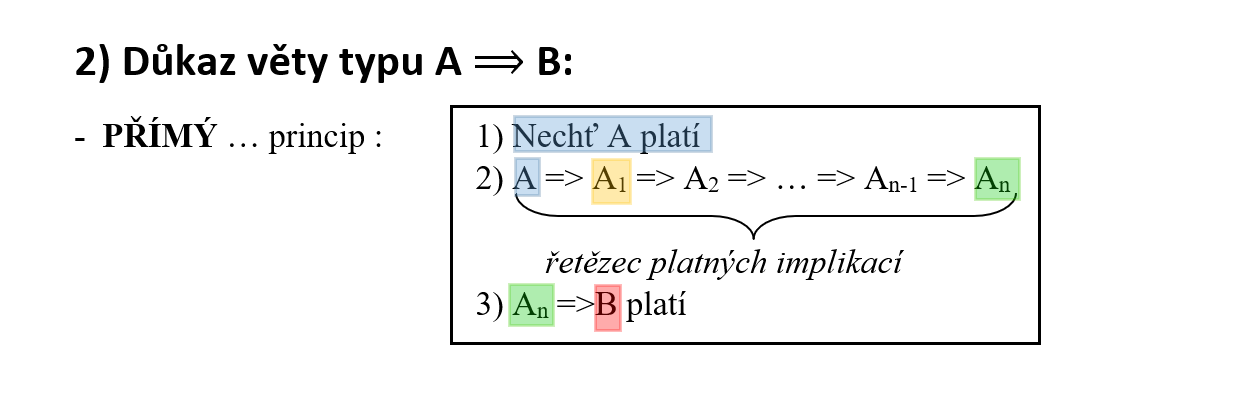
Úloha 7.1.6


Úloha 7.1.7
Dokažte: Pro každé přirozené číslo n platí: je-li n liché, pak je i $n^2$ liché.

NEPŘÍMÝ
… princip založen na ekvivalenci dané implikace $A \Rightarrow B$ a její obměny $\neg B \Rightarrow \neg A$. Obměněná implikace $\neg B \Rightarrow \neg A$ se dokazuje přímo.
Úloha 7.1.8
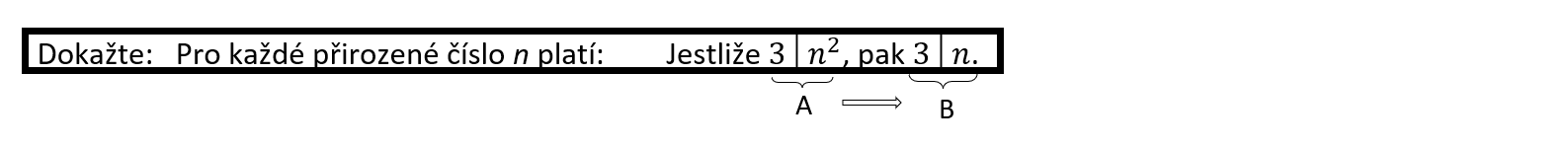

Úloha 7.1.9



Úloha 7.1.10
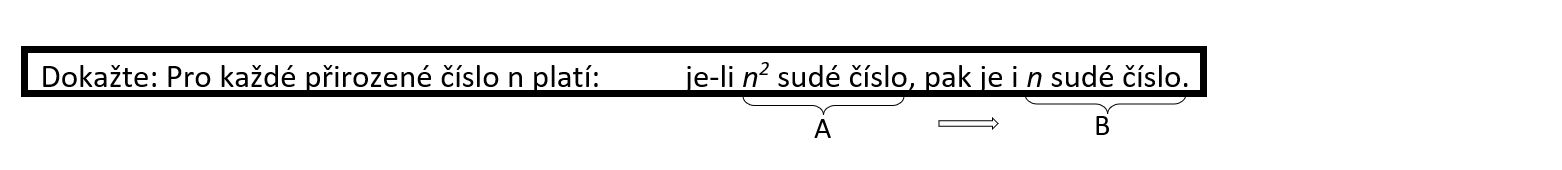




Úloha 7.1.11
Dokažte užitím matematické indukce: $\forall n \in N: 1+2+3+ \dots +n= \frac{n \cdot (n+1)}{2}$.


Úloha 7.1.12

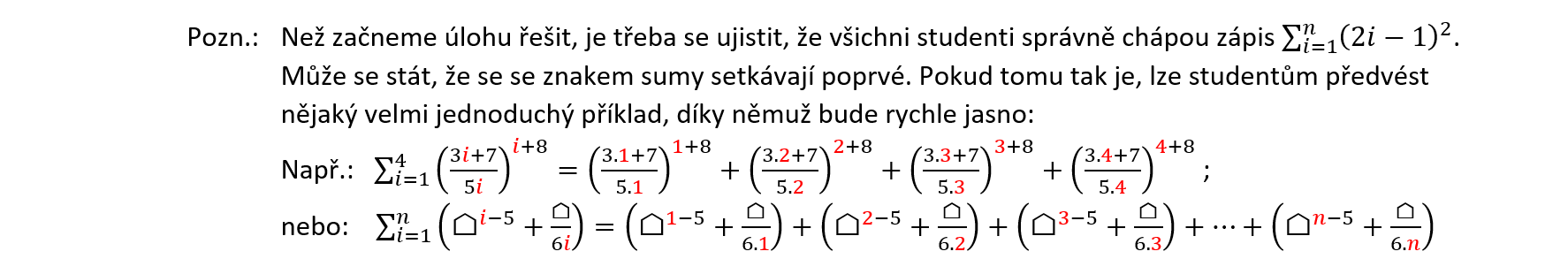
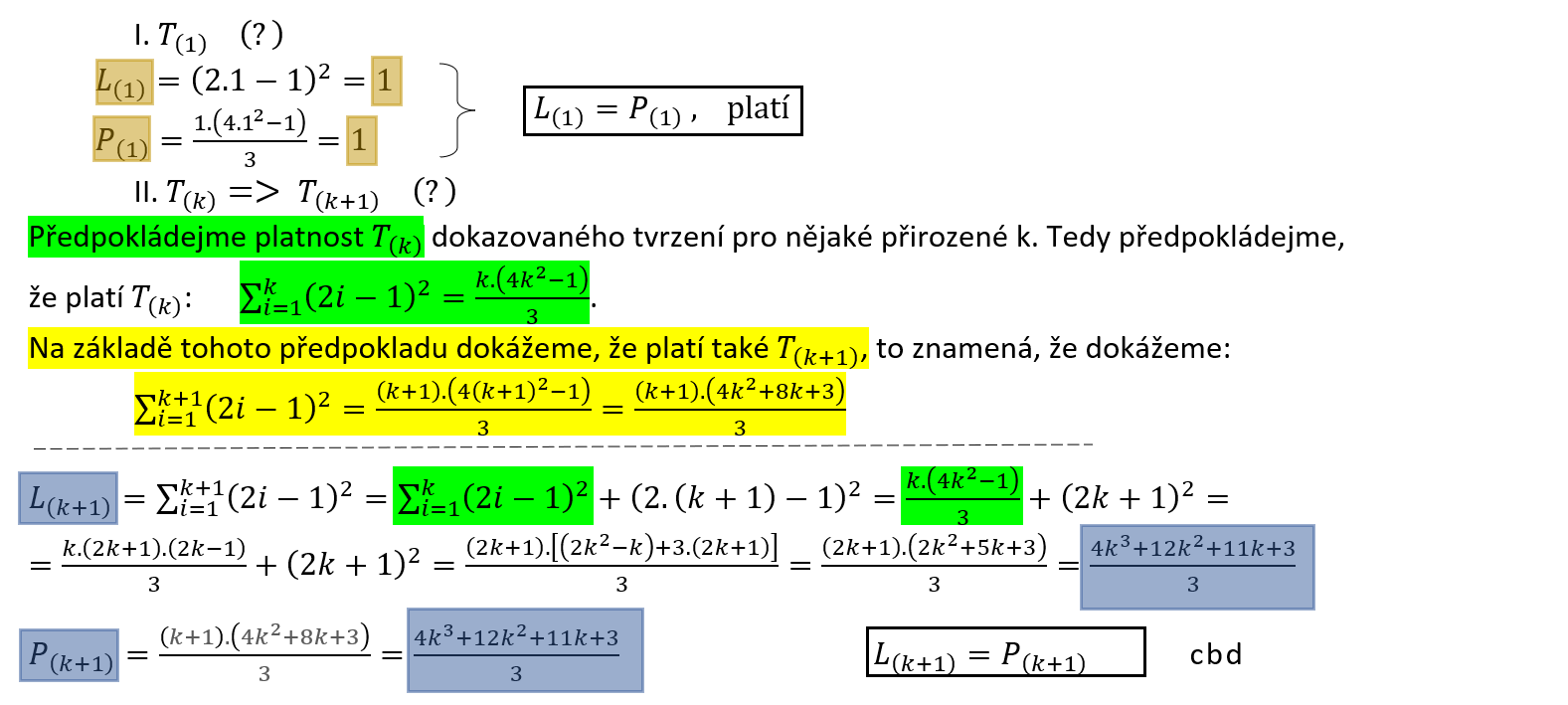
Úloha 7.1.13
Dokažte užitím matematické indukce: $\forall n \in N:4 | (n^4 + 6n^3 + 11n^2 + 6n).$

Úloha 7.1.14
Dokažte užitím matematické indukce: $\forall n \in N:5 | (2^{4n+3} -3)$.

Úloha 7.1.15
Dokažte užitím matematické indukce: $\forall n \in N:36 | (7^n -6n-1)$.

Pozn.: Učitel by měl rozhodně trvat u svých studentů na tak podrobných zápisech, jaké byly použity u výše uvedených důkazů. Pokud studenti dokážou zapsat, kdy co předpokládáme a kdy co dokazujeme, učitel vidí, že postupu rozumí. Aby to po nich ale mohl chtít, musí je to naučit tím, že studenti od něj vidí precizní, přehledné a kompletní zápisy. Může studentům pro zpřehlednění důkazu doporučit, a sám to vždy dodržovat, aby si platný předpoklad vybarvovali třeba zeleně (představuje zelenou na cestě k úspěšnému dokončení důkazu) a zeleně si pak vybarvili i místo, kde ten předpoklad použili v důkazu implikace.
Základní poznatky
Úloha 7.1.16
Dokažte, že součet vnitřních úhlů v trojúhelníku je 180° .
Úloha 7.1.17
Je dána kružnice $k$ s průměrem $AB$. Dokažte větu: Je-li $X$ libovolný bod kružnice k různý od bodů $A$, $B$, pak úhel $AXB$ je pravý.
Typové příklady standardní náročnosti
Úloha 7.1.17
Dokažte: $\forall n \in N:6|(n^3+5n)$
- přímým důkazem (užitím vytknutí dělitele)
- matematickou indukcí
Úloha 7.1.18
Dokažte: $\forall n \in N:4|n^2 \Rightarrow 2|n$
- nepřímým důkazem
- sporem
Úloha 7.1.19
Dokažte matematickou indukcí:
- $\forall n \in N:1 \cdot 2 + 2 \cdot 3 + 3 \cdot 4 + \dots n(n+1) =$ $\frac{1}{3}n(n+1)(n+2)$
- $\forall n \in N: \sum^n_{i=1}\frac{i-2}{3}=\frac{n}{6}(n-3)$
Úloha 7.1.20
Dokažte platnost vzorce
- pro výpočet n-tého členu aritmetické posloupnosti pomocí prvního;
- pro výpočet součtu prvních n členů aritmetické posloupnosti.
Rozšiřující cvičení
Úloha 7.1.21
Dokažte, že prvočísel je nekonečně mnoho.
Sporem.