Planimetrie
Obsah oddílu
Podobná zobrazení
Stručný přehled teorie
PODOBNOST
- Dva rovinné útvary jsou podobné, jestliže poměry délek všech dvojic odpovídajících si úseček těchto útvarů se rovnají témuž číslu $k\gt 0$ ($k$ – poměr podobnosti).
- Každé dva odpovídající si úhly podobných útvarů jsou shodné.
Podobnost útvarů se opírá o podobnost trojúhelníků
- Věty o podobnosti trojúhelníků (sss, sus, uu, Ssu).
- Užití podobnosti trojúhelníků (řešení některých praktických úloh, redukční úhel, ….).
PODOBNÉ ZOBRAZENÍ
- Podobné zobrazení je takové zobrazení, které každým dvěma bodům $X$, $Y$ (vzorům) přiřazuje body
$X'$, $Y'$ (obrazy) tak, že $\left\lvert X'Y'\right\rvert=k\cdot\left\lvert XY\right\rvert$, kde $k$ – poměr podobnosti ($k\gt 0$)
STEJNOLEHLOST (HOMOTETIE) $H_{(S,K)}$
- Druh podobného zobrazení.
- Je určena středem stejnolehlosti $S$ a koeficientem stejnolehlosti $\kappa \left(\kappa \in R - \{0\}\right)$.
Body roviny zobrazuje takto:
- Středu $S$ přiřazuje tentýž bod $S$. Tedy $H_{S,K}\!:\boldsymbol{S\rightarrow}S'=S$
($S$ – jediný samodružný bod). - Každému bodu $X$ roviny různému od $S$ přiřazuje bod $X'$ tak, že:
- je-li $\kappa\gt 0$, pak $X'\in\mapsto SX$ a $\left\lvert SX'\right\rvert=\kappa\cdot\left\lvert SX\right\rvert$
- je-li $\kappa\lt 0$, pak $X'\in(\mapsto SX)'$ a $\left\lvert SX'\right\rvert=\left\lvert\kappa\right\rvert\cdot\left\lvert SX\right\rvert$
Některé vlastnosti stejnolehlosti:
- Samodružné přímky jsou všechny přímky procházející středem stejnolehlosti.
- Stejnolehlé úsečky (přímky) jsou vzájemně rovnoběžné.
- Stejnolehlost zachovává poměr délek úseček.
STEJNOLEHLOST KRUŽNIC
- Každé dvě nesoustředné kružnice s různými poloměry jsou dvěma způsoby stejnolehlé (nutná znalost konstrukce středů stejnolehlosti).
- Mají-li tyto kružnice společné tečny, pak tyto tečny procházejí příslušnými středy stejnolehlosti (nutná znalost konstrukce společných tečen).
Pozn.: Soustředné kružnice jsou z hlediska stejnolehlosti nezajímavé jednak vzhledem k umístění středu stejnolehlosti do společného středu kružnic a jednak vzhledem k absenci společných tečen, pokud kružnice mají různé poloměry.
Metodika:
S tématem podobnosti se studenti setkali už na základní škole. Měli by tedy chápat, co znamená, že jsou dva útvary $U$ a $U'$ podobné. Měli by vědět, že koeficient podobnosti představuje kladné reálné číslo, které svojí hodnotou určuje, zda v případě, že je $U$ vzor a $U'$ obraz, dochází k zvětšení $(k\gt 1)$ nebo ke zmenšení $(k\lt 1)$.
Pokud jde o využití podobnosti, upřednostňují se na ZŠ zejména jednoduché slovní úlohy typu např.
1) určování výšky objektu na základě délky stínu, který vrhá,
2) určování poměru obvodů nebo obsahů rovinných útvarů, známe-li poměr délek odpovídajících stran.
Využití podobnosti v konstrukčních úlohách se na základní škole omezuje pouze na narýsování jednoduchého útvaru podobného s daným útvarem při daném koeficientu podobnosti a na změnu velikosti úsečky v daném poměru, případně na rozdělení úsečky bodem na dvě části, jejichž délky jsou v daném poměru, přičemž využívají při konstrukci redukční úhel. Nelze však spoléhat na to, že všichni učitelé na ZŠ proberou, případně že si všichni studenti ze ZŠ zapamatují, princip redukčního úhlu.
Tyto skutečnosti by měl zohlednit vyučující při promýšlení obsahu a struktury úvodních hodin probírání tématu Podobnost na střední škole. Redukční úhel představuje velmi užitečný a zároveň jednoduchý prostředek používaný v geometrii relativně často.
Příklad
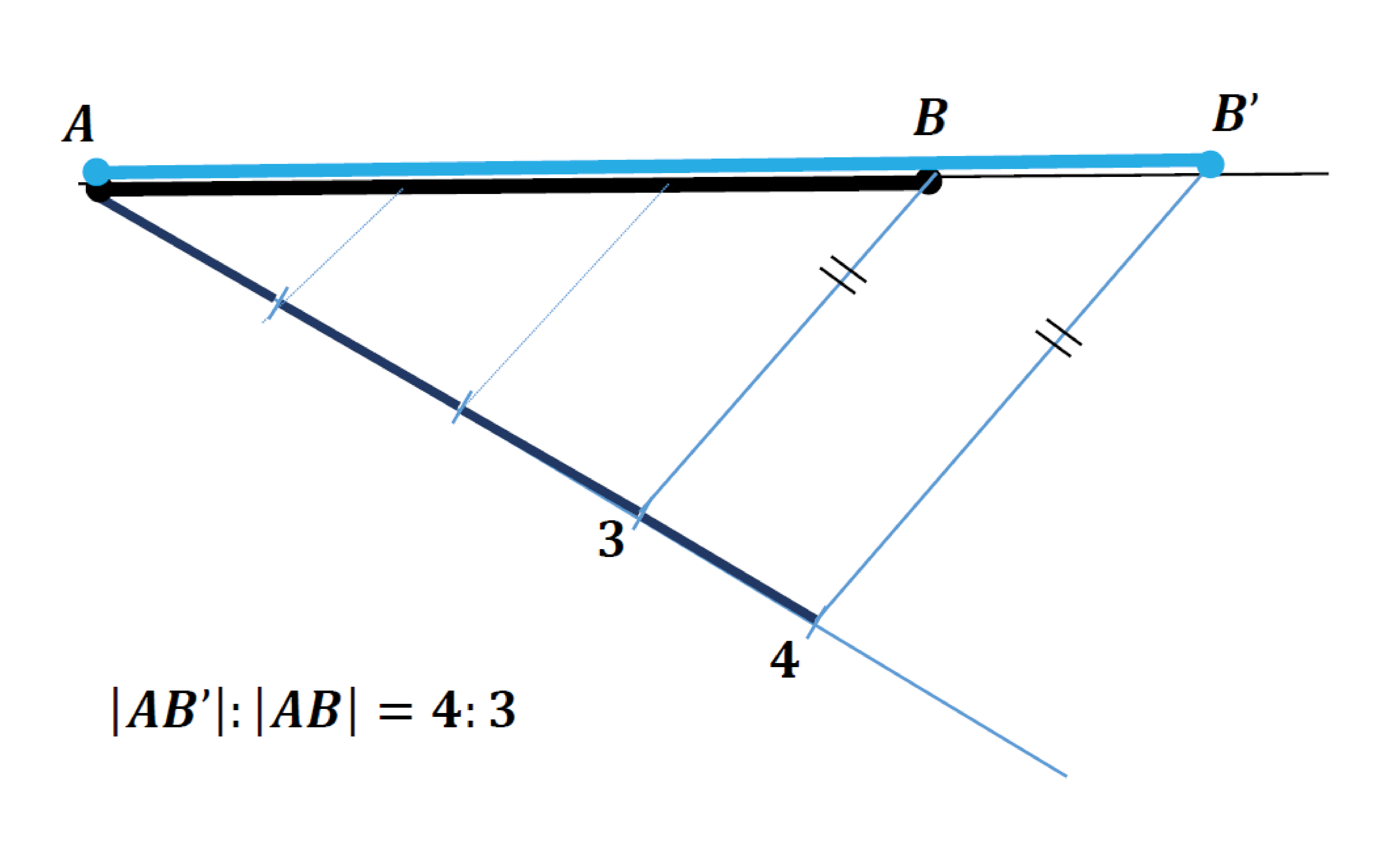
Dána úsečka $AB$, jejíž velikost je $7\,cm$.
- Změňte její velikost v poměru 4:3,
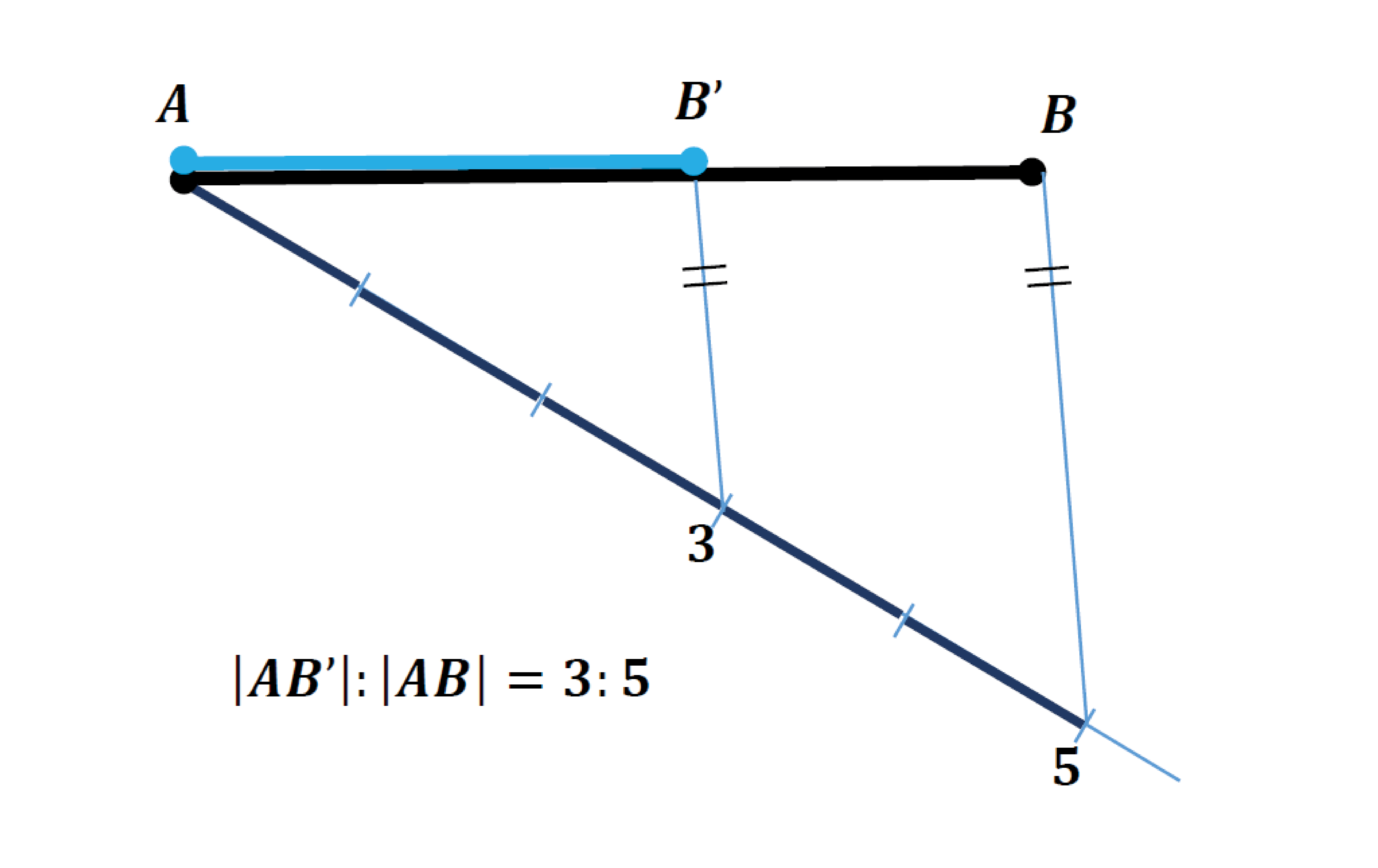
- Změňte její velikost v poměru 3:5,
- Rozdělte ji bodem $C$ na dvě části, jejichž délky jsou v poměru 1:2.
Učitel by měl se studenty nejen zopakovat mechanismus využití redukčního úhlu, ale zastavit se krátce nad vysvětlením jeho principu, který využívá podobných trojúhelníků.
Metodika:
Těžiště tématu Podobnost pak na střední škole spočívá zejména v důkladném seznámení studentů s principem a využitím stejnolehlosti. Stejnolehlost je pro studenty na střední škole zcela nový pojem, s kterým se doposud nesetkali. Dá se předpokládat, že už prvním problémem bude pro ně skutečnost, že stejnolehlé útvary jsou podobné s vždy kladným koeficientem podobnosti $\boldsymbol k$, ale koeficient stejnolehlosti $\boldsymbol\kappa$ může být jak kladný, tak i záporný. Je na vyučujícím, aby rozdíl mezi koeficientem podobnosti a koeficientem stejnolehlosti dokázal studentům precizně vysvětlit.
Než se pak přistoupí k úlohám, jejichž řešení je založeno na využití stejnolehlosti, musí se studenti naučit ve stejnolehlostech s různými koeficienty a různě umístěnými středy stejnolehlosti zobrazovat všechny základní útvary – body, přímky, n-úhelníky, kružnice. Vyučující by měl přitom využívat situace a vést studenty k tomu, aby si všímali vlastností zobrazovaných útvarů, aby je dokázali popisovat, formulovat jevy, zdůvodňovat, dokazovat.
Stejnolehlosti kružnic je dobré věnovat celou vyučovací hodinu a k práci se stejnolehlými kružnicemi a středy stejnolehlosti přidat i konstrukce společných tečen (zopakovat přitom konstrukci tečny z bodu ke kružnici užitím Thaletovy kružnice!!!).
Příklad
Jsou dány dva body $O_1$ a $O_2$, $\left\lvert O_1O_2\right\rvert = 6\,cm$ a dále dvě kružnice $k_1(o_1; r_1=3\,cm)$, $k_2(o_2; r_2=3\,cm)$. Nalezněte všechny středy stejnolehlostí těchto kružnic a všechny jejich společné tečny.
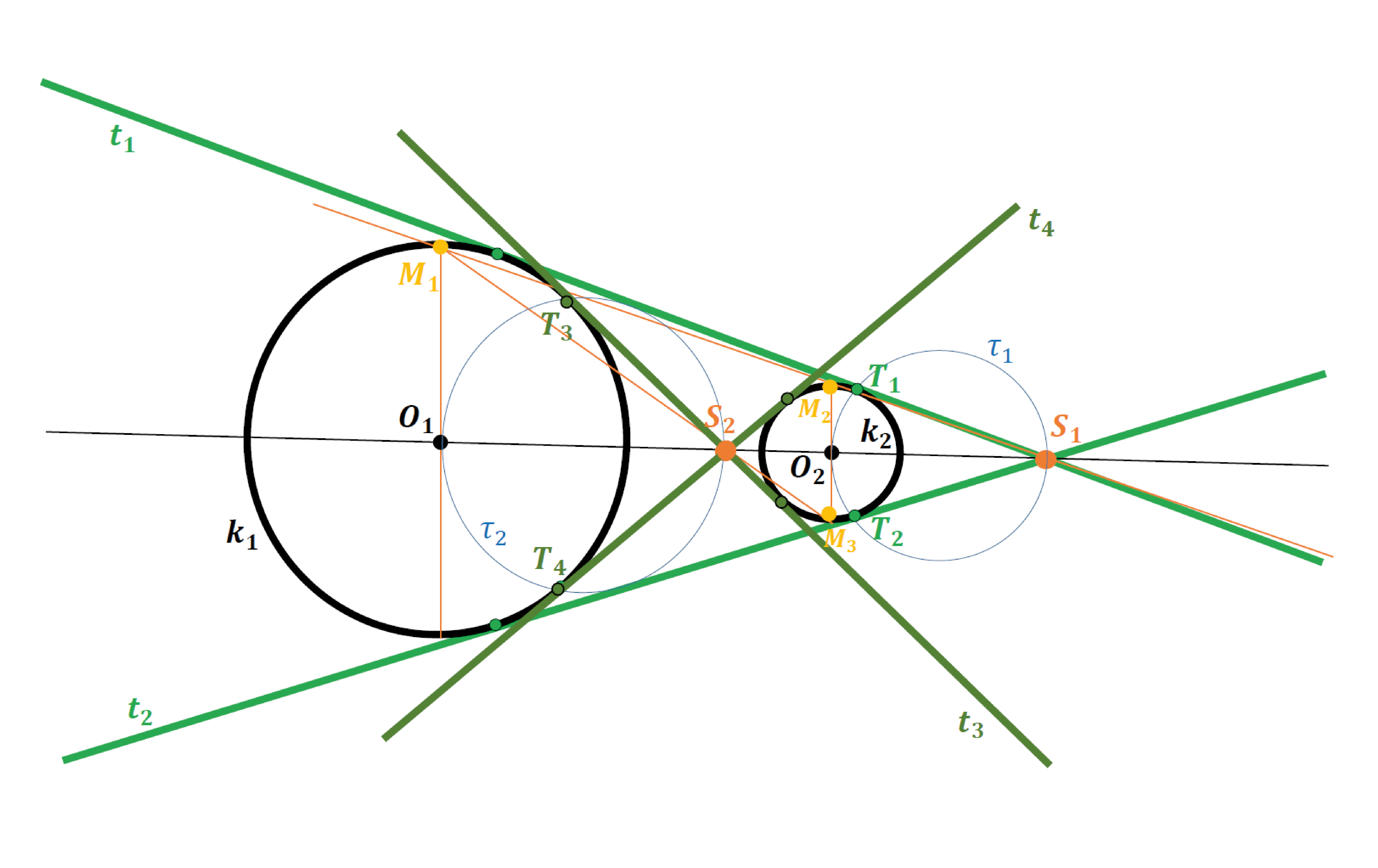
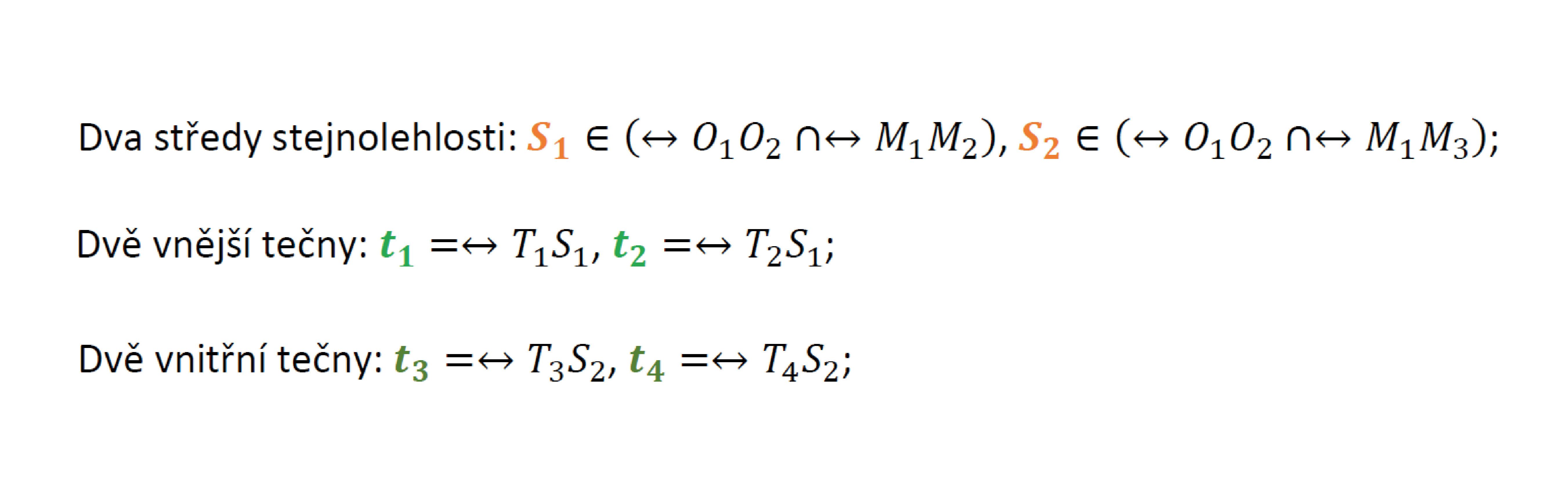
Pozn.: náčrty situací s ostatními vzájemnými polohami kružnic – zvážit podle časových možností …
Metodika:
Většinu úloh souvisejících ve středoškolské planimetrii se stejnolehlostí lze podobně jako je tomu u shodných zobrazení rozdělit do dvou základních skupin. Jejich odlišujícím prvkem je zejména rozbor, který je pro každou z těchto skupin typický. Navíc pokud se rozbor správně a precizně zapíše, může obsahovat vždy na obdobném místě „pokyn“ k prvnímu kroku a tím k vykročení do řešení úlohy.
Úlohy prvního typu:
(Mají třířádkový rozbor, přičemž druhý řádek představuje zmiňované „vykročení“ do řešení úlohy).
Příklad
Je dán dutý úhel $\sphericalangle AVB$ a bod $M$, který leží uvnitř tohoto úhlu. Bodem $M$ veďte přímku $p$ tak, aby platil vztah $\left\lvert MX\right\rvert:\left\lvert MY\right\rvert =1:2$, kde $X$, $Y$ jsou průsečíky přímky $p$ s rameny $\to VA$ a $\to VB$.
Náčrt:
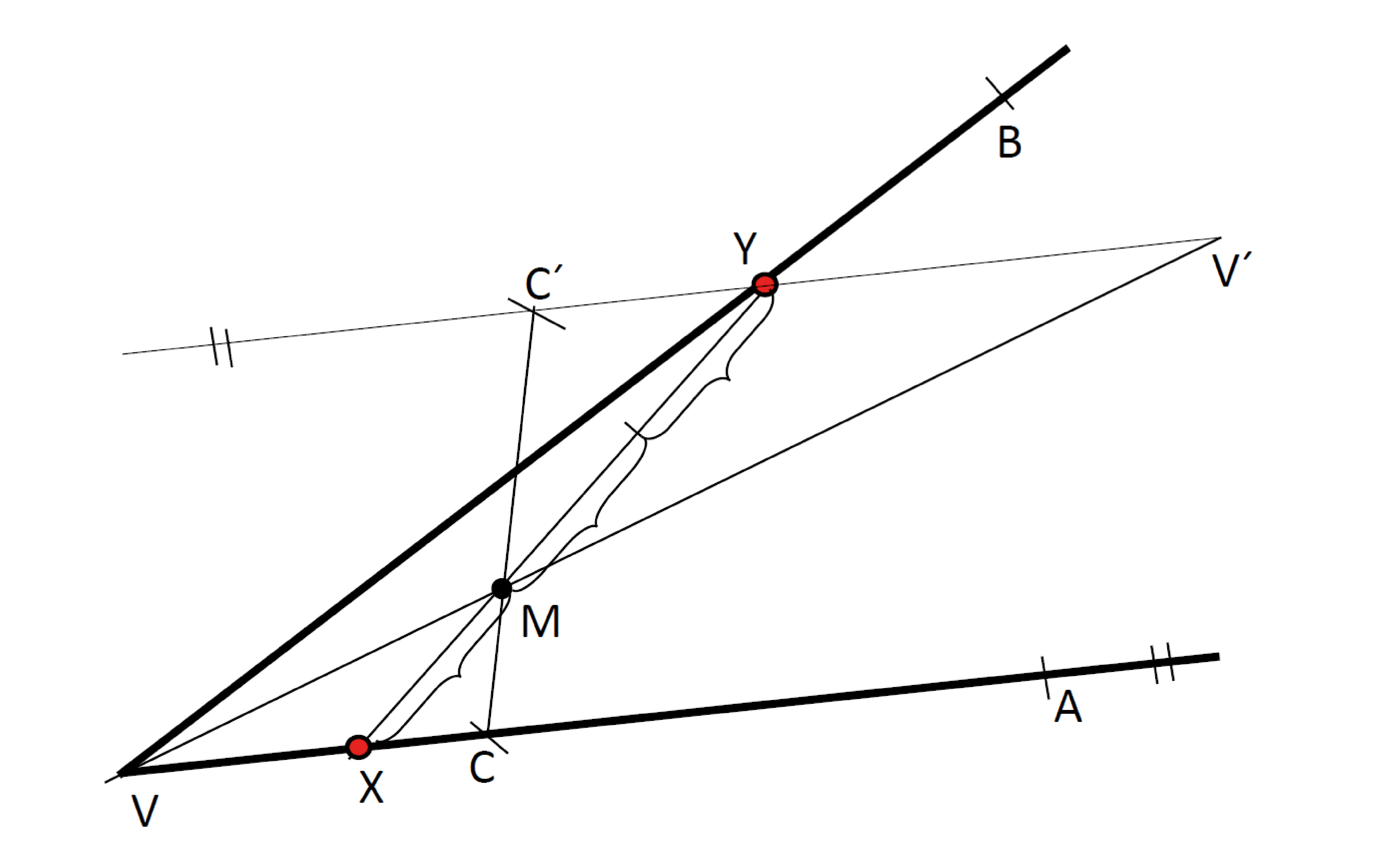
Rozbor:
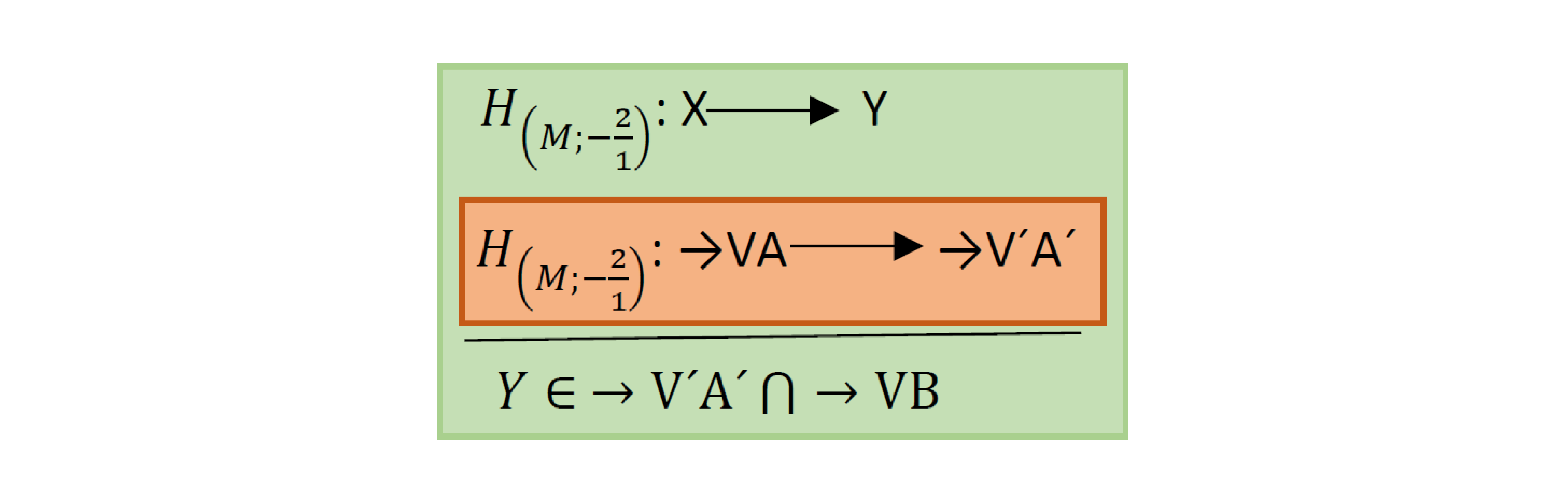
$C$ je libovolný bod polopřímky $\to VA$, použijeme jej pro konstrukci jejího obrazu místo bodu $A$, je-li $A$ umístěn tak, že $A'$ leží v „nevhodném“ místě …
Skutečná výchozí situace:

Víme, že $Y$ je obraz $X$ ve stejnolehlosti $H_{\left(M;-\frac{2}{1}\right)}$ . Protože ale nevíme, kde se na polopřímce $\to VA$ bod $X$ nachází, zobrazíme celou polopřímku $\to VA$ – každý bod z $\to VA$ si „najde“ svůj obraz na $\to V'A'$ a $X$ si „najde“ svůj obraz $Y$ v průsečíku $\to V'A'\,\cap \to VB$.
Konstrukce:
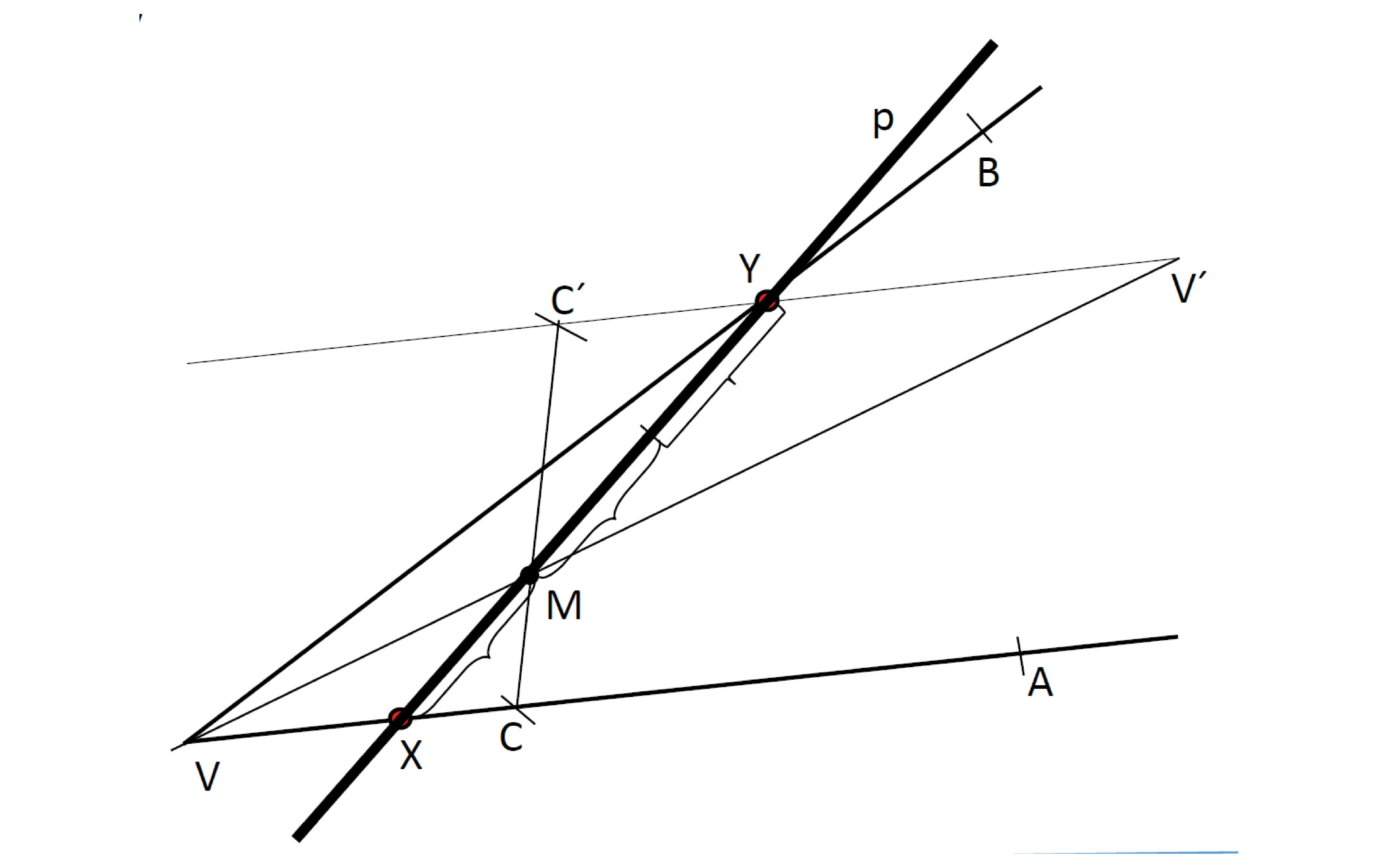
Postup:
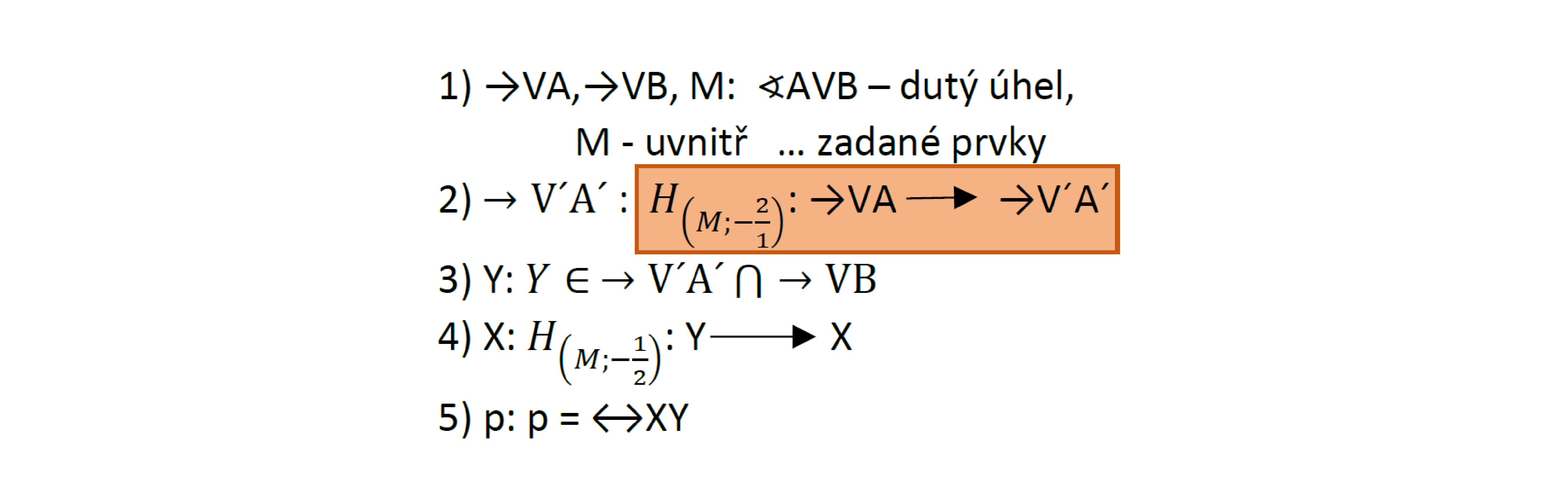
Úloha 3.3.1
Je dána kružnice $k(S,r)$ a bod $M$, který leží uvnitř kružnice $k$. Bodem $M$ veďte tětivu $XY$ tak, aby platil vztah $\left\lvert XM\right\rvert :\left\lvert YM\right\rvert =2:3$.
Náčrt:
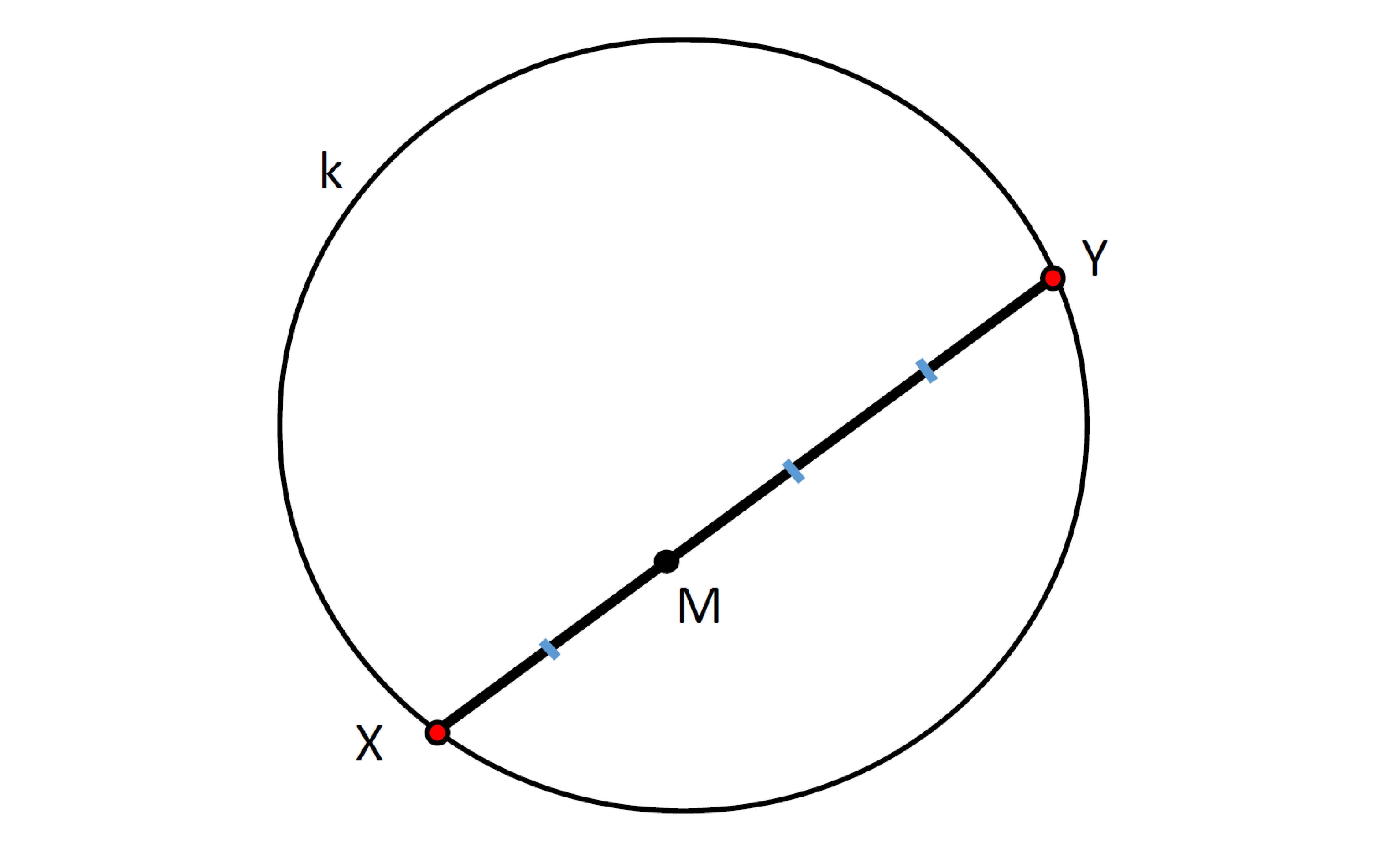
Rozbor:
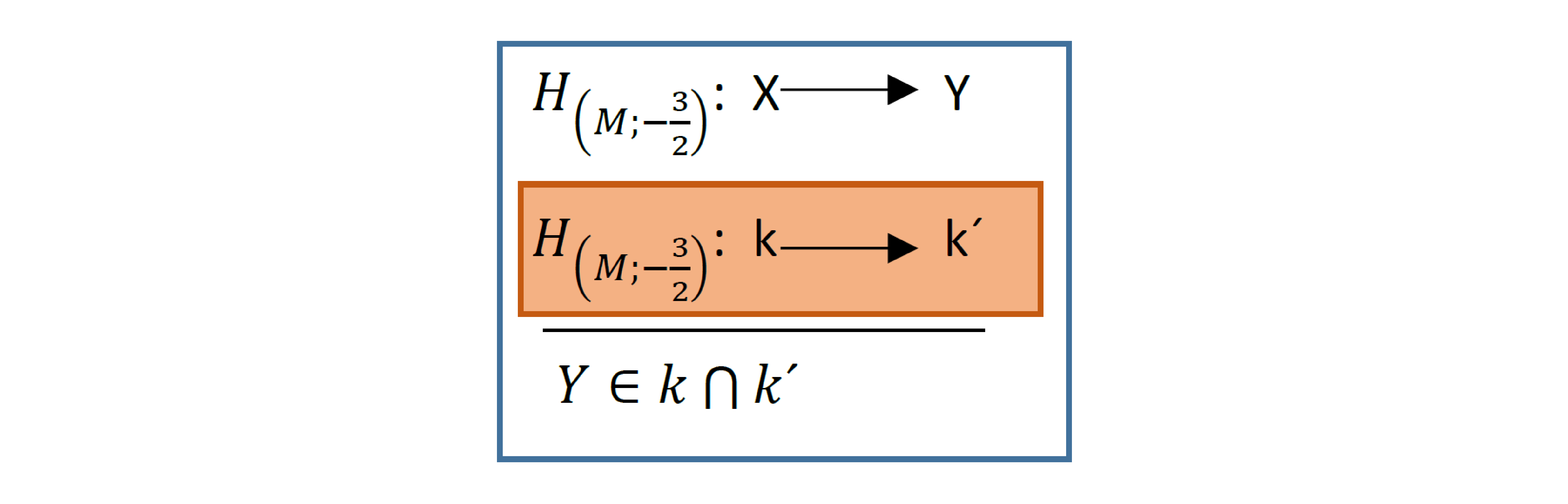
Úloha 3.3.2
Je dána kružnice $k(S,r)$ a bod $A$, který leží vně kružnice $k$. Bodem $A$ veďte sečnu $p$ kružnice $k$ tak, aby platil vztah $\left\lvert AY\right\rvert =3\left\lvert AX\right\rvert$, kde $X$ a $Y$ jsou průsečíky přímky $p$ s kružnicí $k$.
Náčrt:
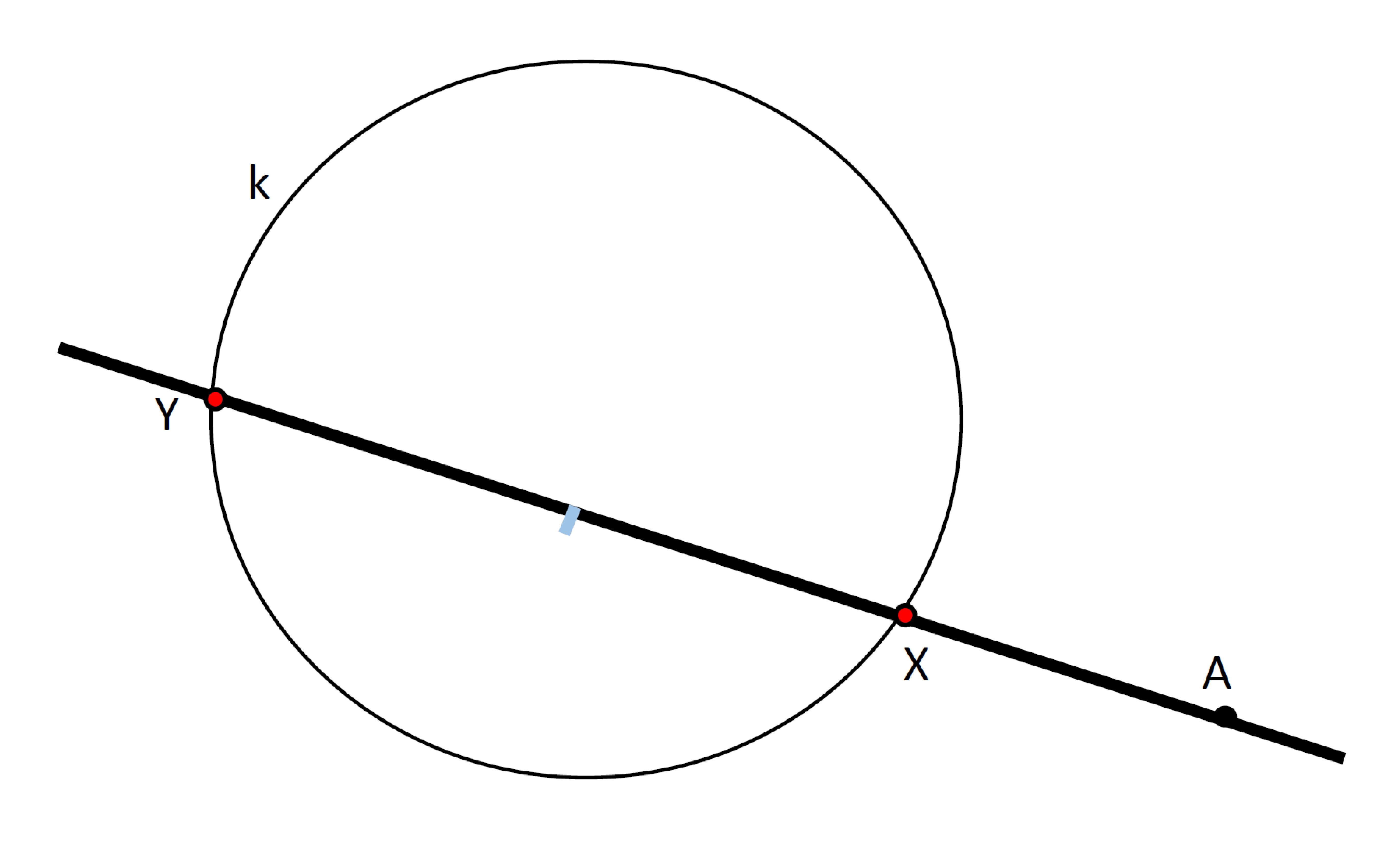
Rozbor:
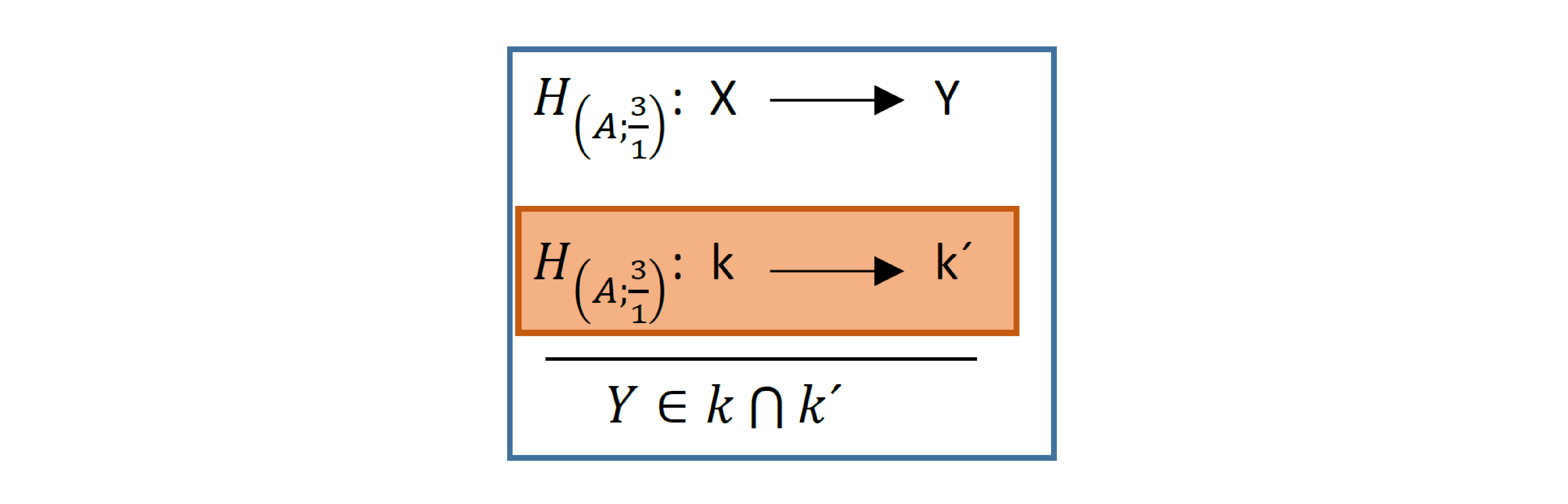
Úlohy druhého typu:
Vyžadují k zadaným prvkům sestrojit rovinný útvar $U$, který má splňovat celou řadu vlastností. Všechny najednou ovšem nelze splnit okamžitě. Je třeba navést studenty na myšlenku, že je v našich silách sestrojit pomocný útvar $U'$, který většinu vlastností, zpravidla až na jednu, splňuje. K požadovanému útvaru $U$ se pak dostaneme užitím stejnolehlosti aplikované na pomocný útvar $U'$. Výběr vlastnosti, které se při konstrukci pomocného útvaru vzdáme, by se mohl zdát obtížným. Je však zcela logický a studentům by neměl dělat při dobrém počátečním vysvětlení problémy. Jestliže se požadovaný útvar $U$ získá z $U'$ užitím stejnolehlosti, je jasné že musí už $U'$ vykazovat požadovaný tvar. Vlastnost, které se při konstrukci $U'$ vzdáme, tedy nesmí mít na tvar výsledného útvaru vliv. Rozbor úloh druhého typu je obsáhlejší, ale i v něm se vždy na obdobném místě vyskytuje řádek odpovídající „vykročení“ do řešení úlohy.
Příklad
Sestrojte $\bigtriangleup ABC$, je-li dáno: $a:b:c = 2:3:4$ a $v_a = 5\,cm$.
Náčrt:
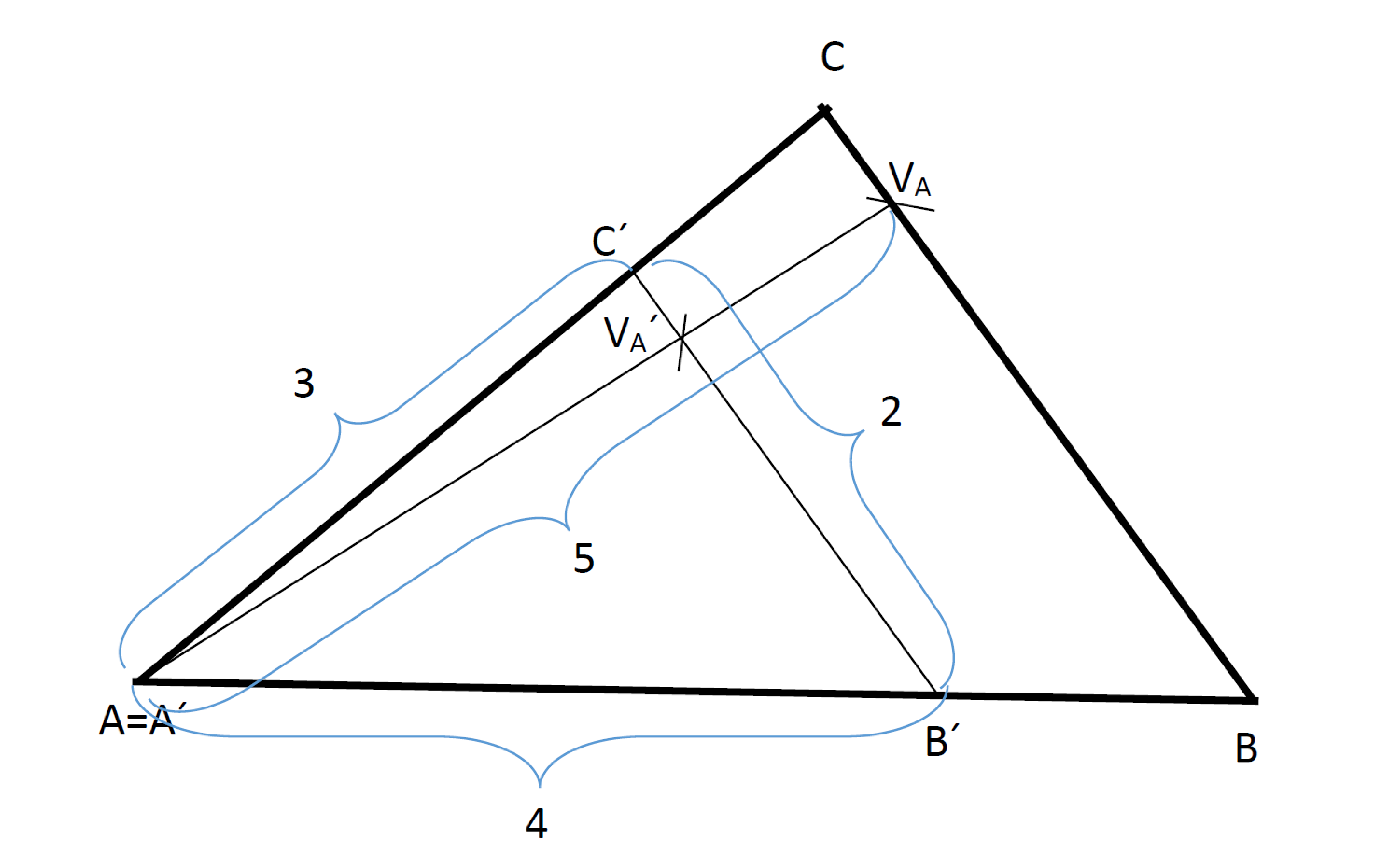
Rozbor:
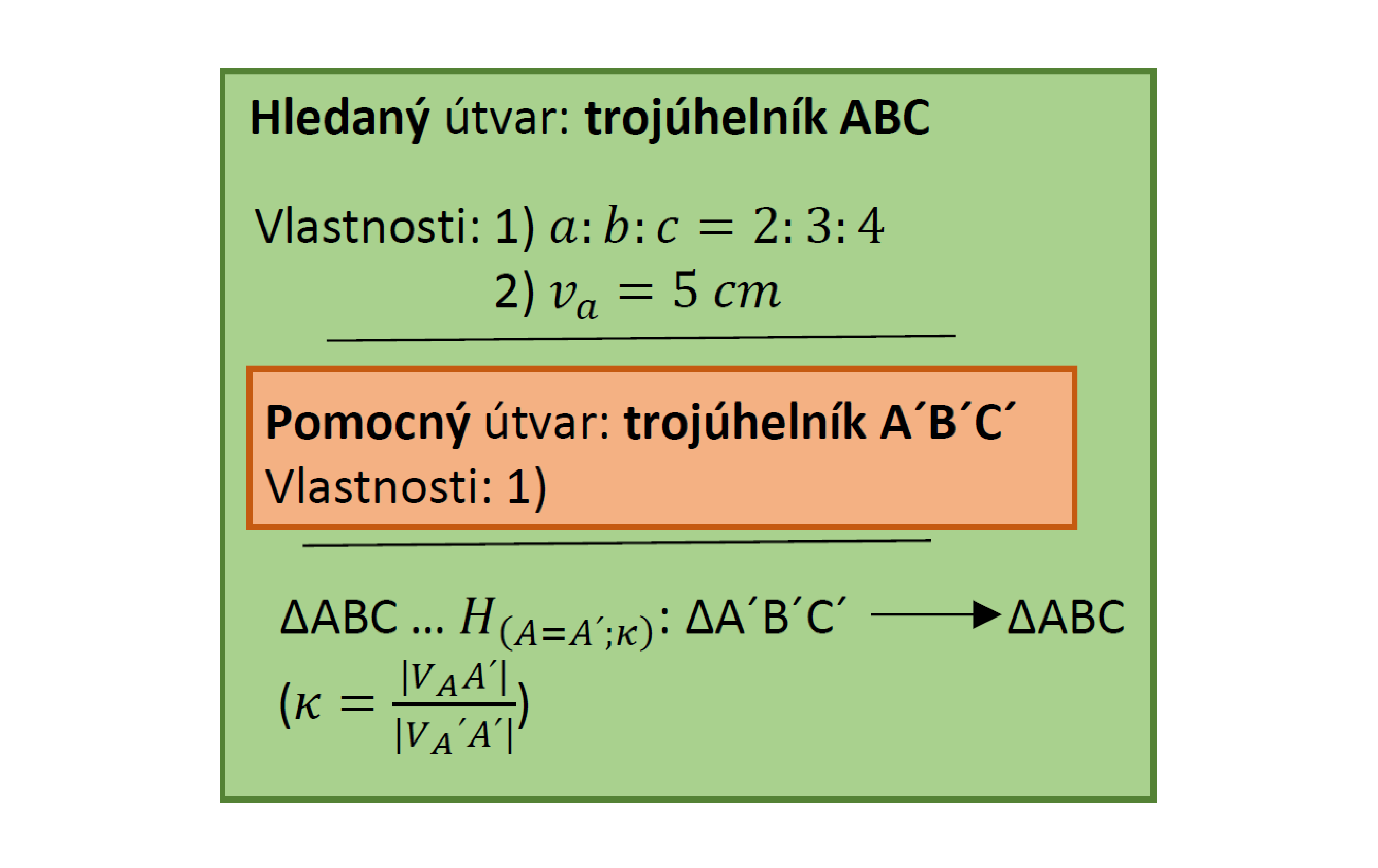
Konstrukce:
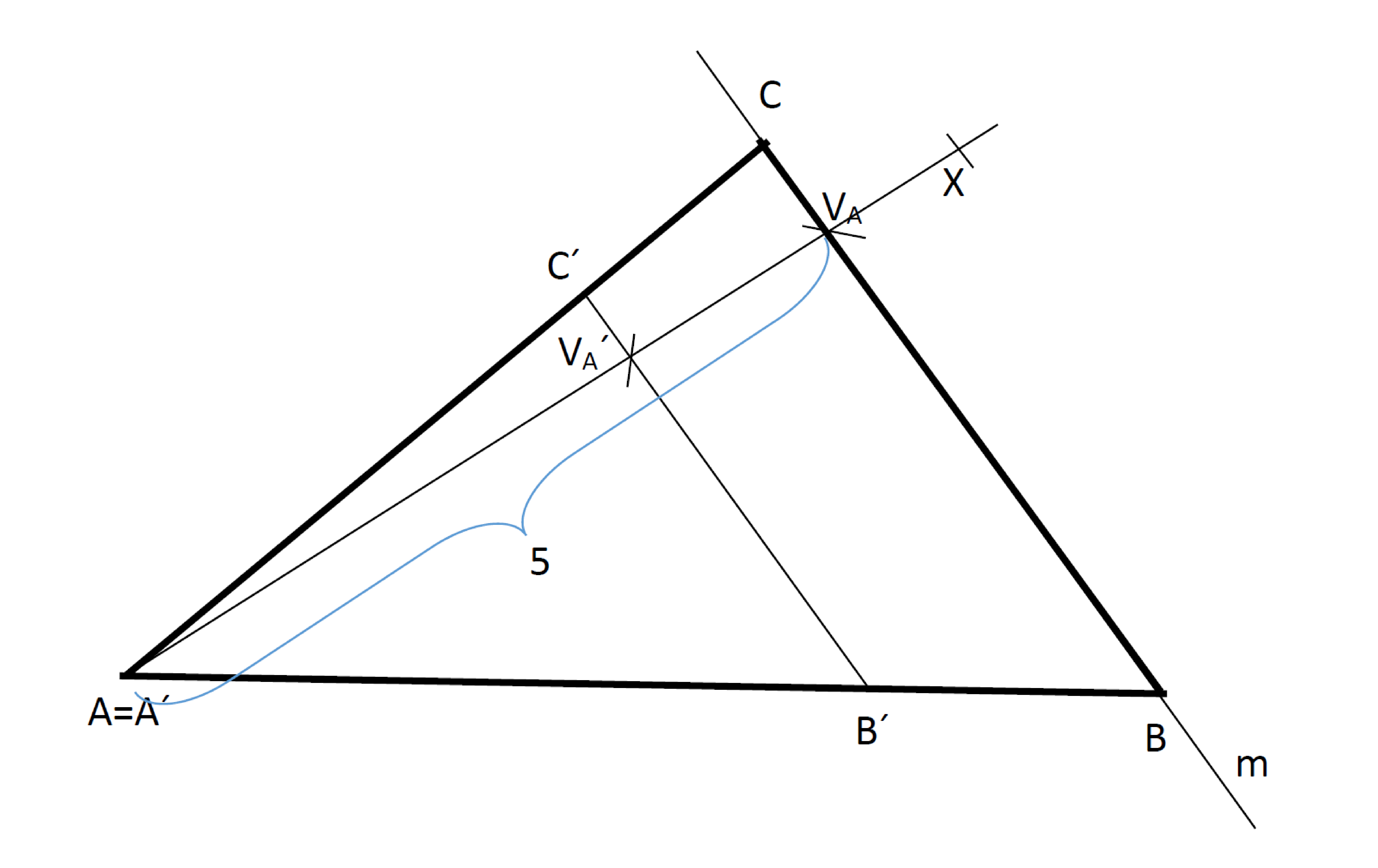
Postup:
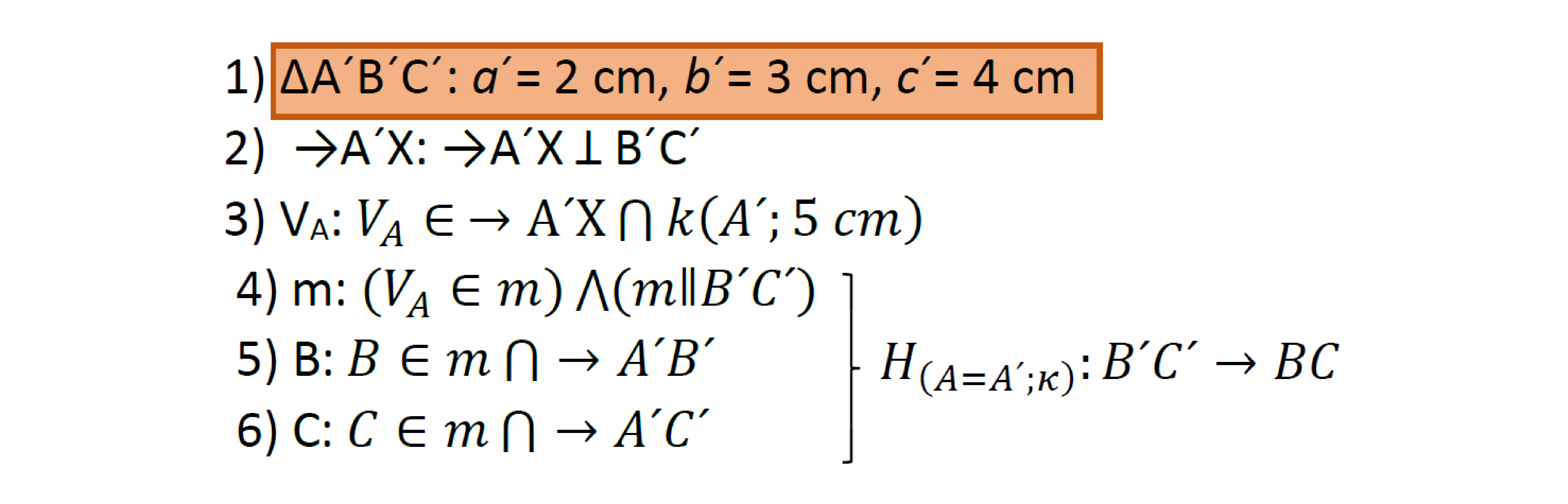
Úloha 3.3.3
Sestrojte $\bigtriangleup ABC$, je-li dáno: $\alpha ,\beta,t_c.$
Náčrt:
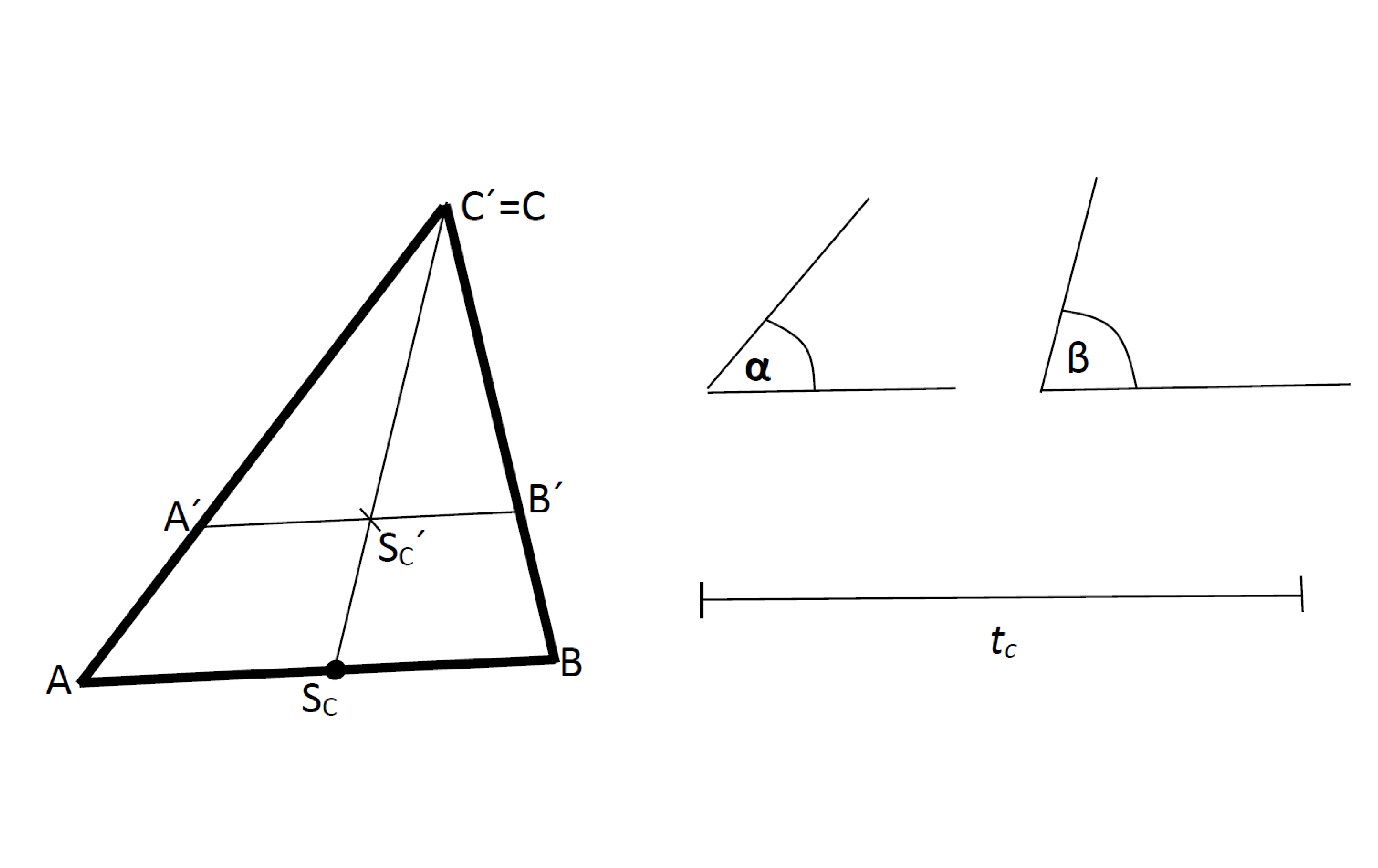
Rozbor:
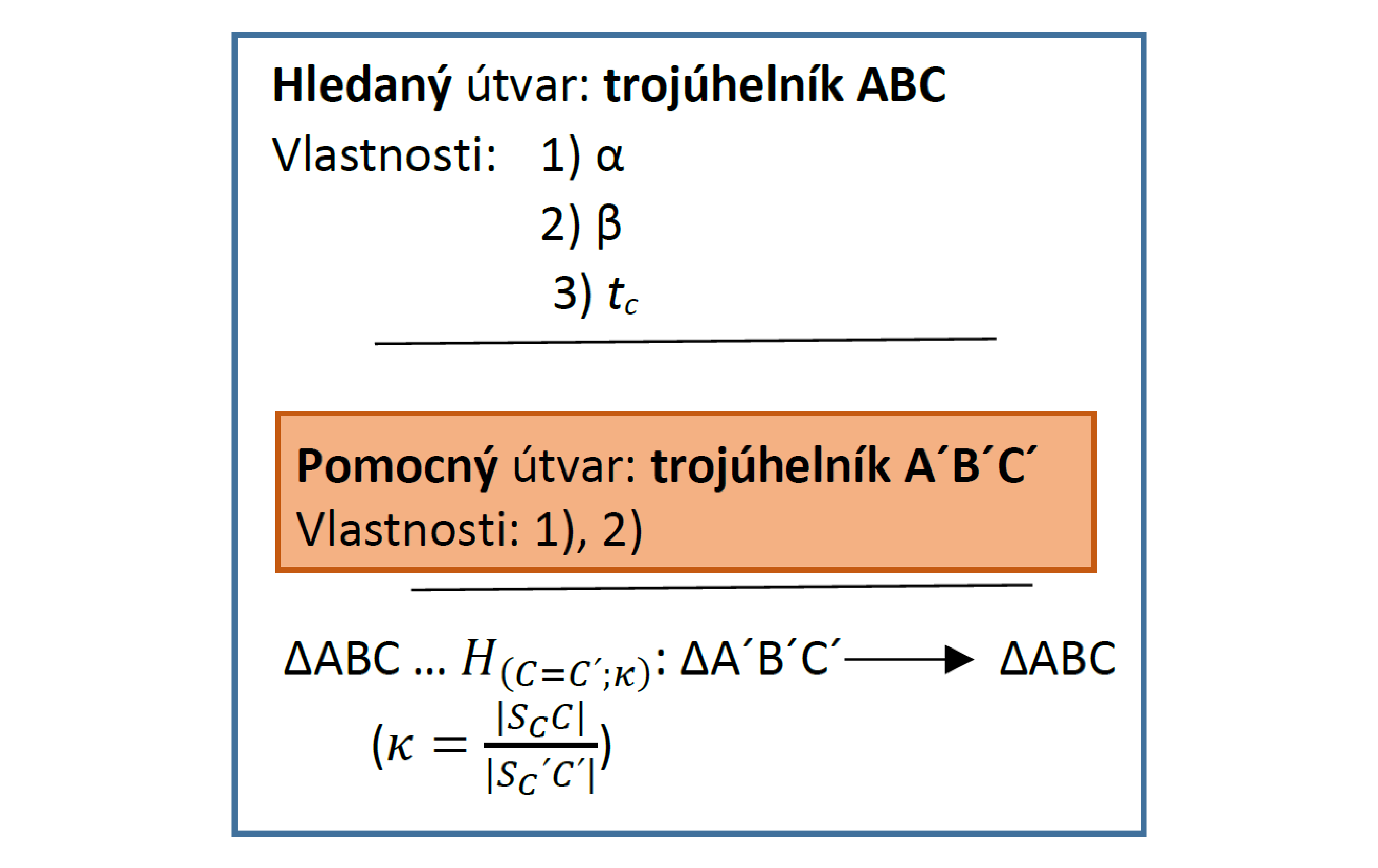
Úloha 3.3.4
Ostroúhlému $\bigtriangleup ABC$ vepište obdélník $KLMN$ tak, aby $KL\subset AB$, $M\in BC$, $N\in AC$, a aby platilo: $\left\lvert KL\right\rvert :\left\lvert LM\right\rvert = 3:4$.
Náčrt:
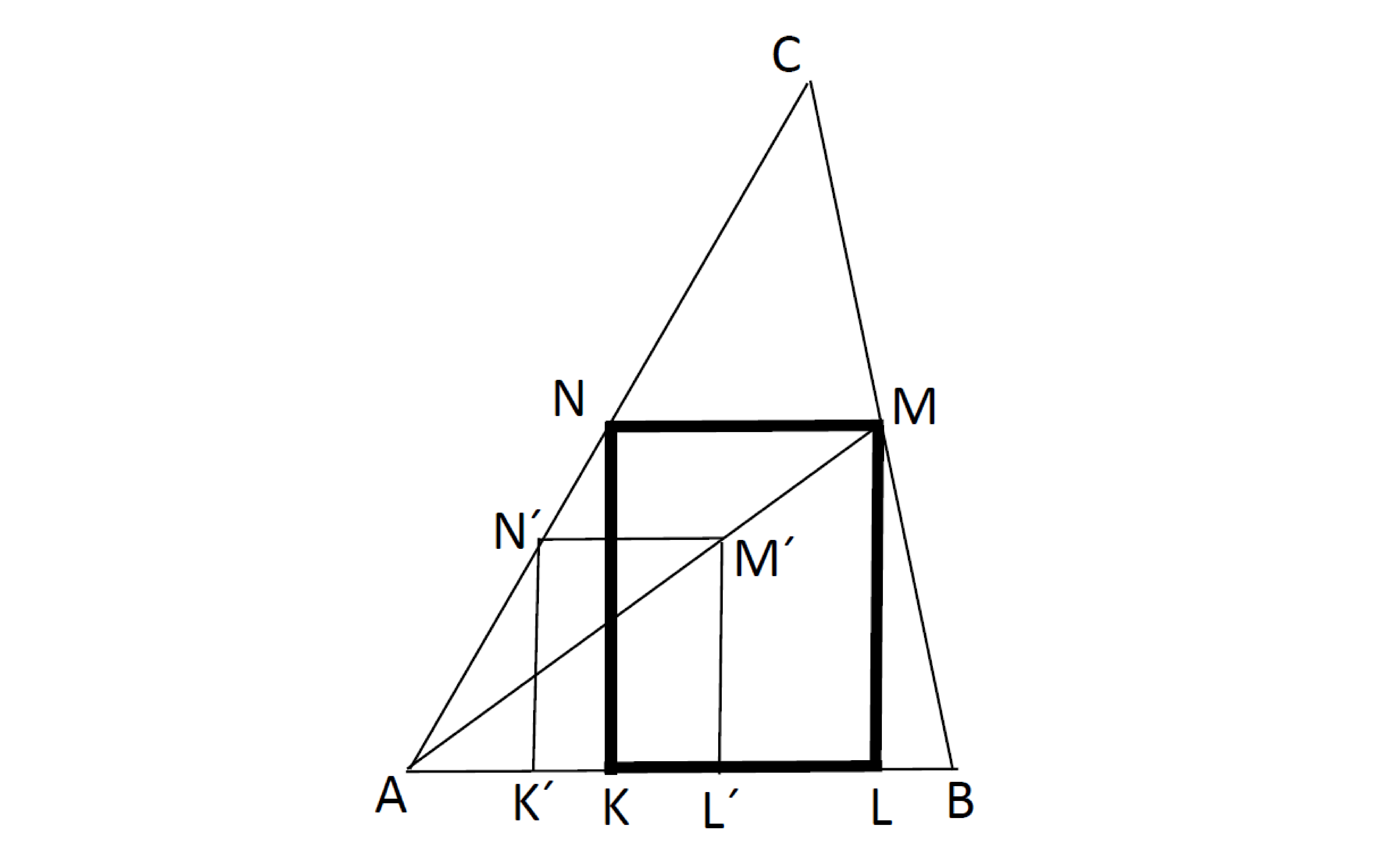
Rozbor:
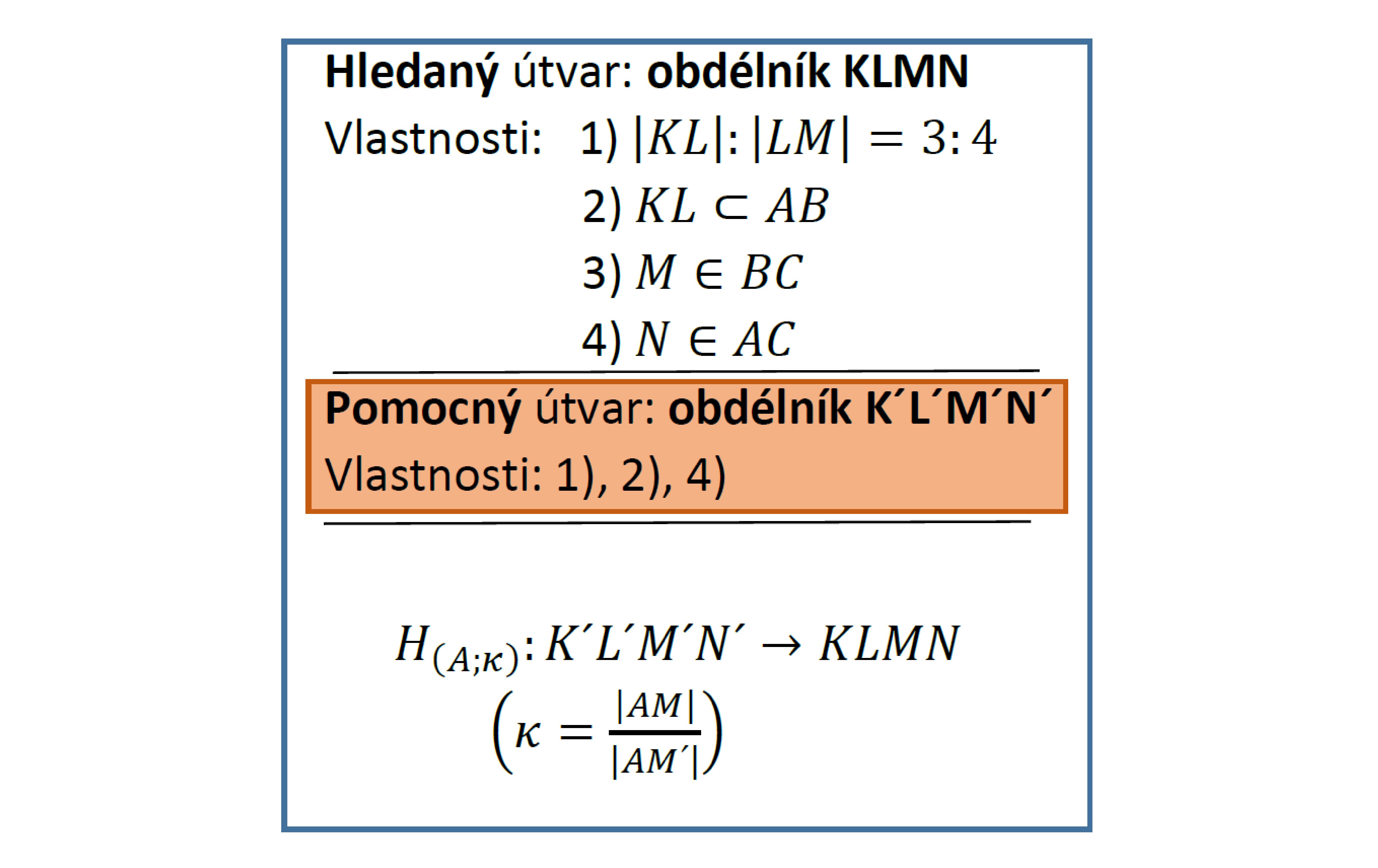
Úloha 3.3.5
Je dán ostrý úhel $AVB$ a bod $Q$ tak, že leží uvnitř tohoto úhlu. Sestrojte půlkružnici $k$ tak, aby procházela bodem $Q$, dotýkala se polopřímky $VA$ a měla průměr $RP$ na polopřímce $VB$.
Náčrt:
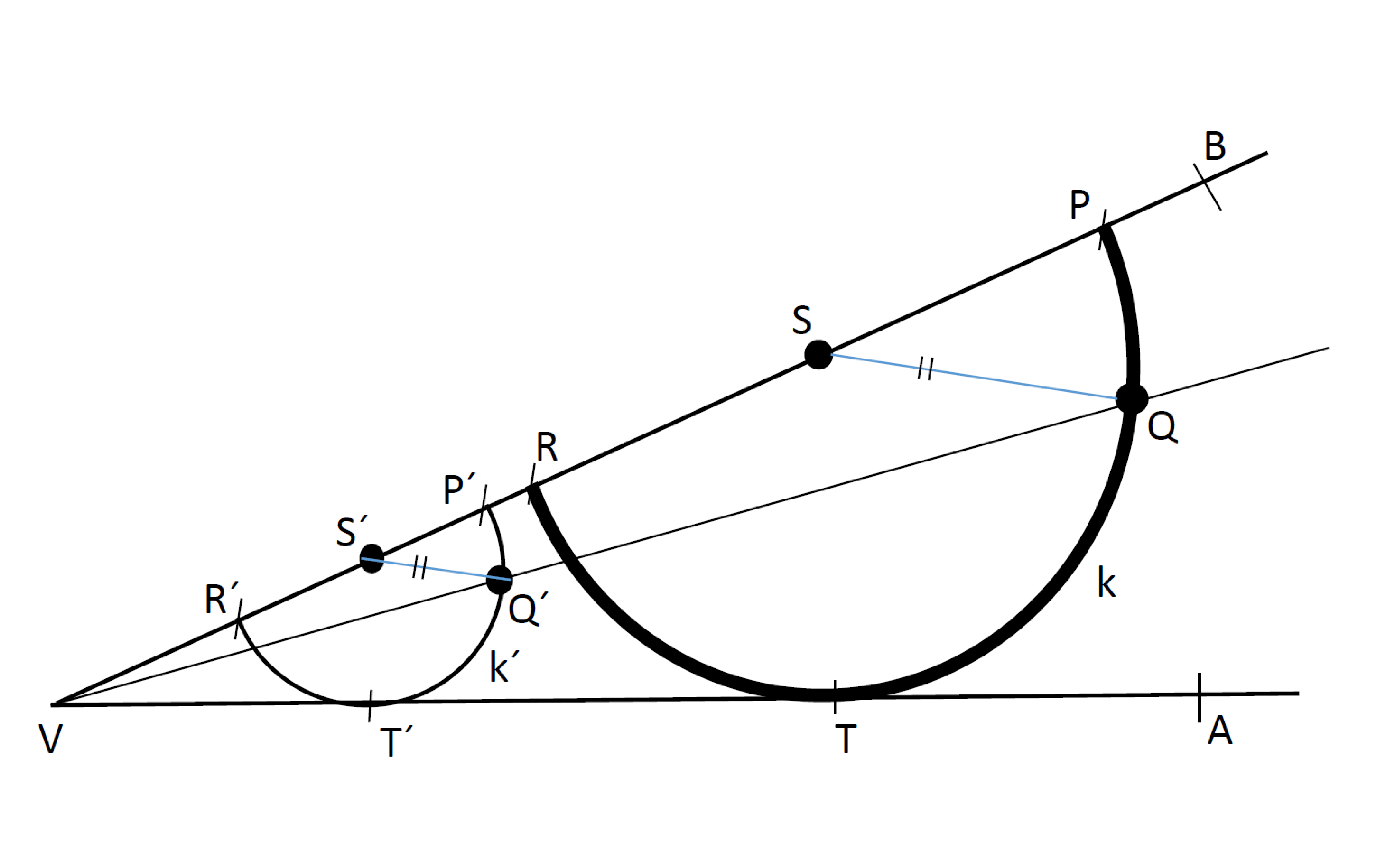
Rozbor:

Úloha 3.3.6
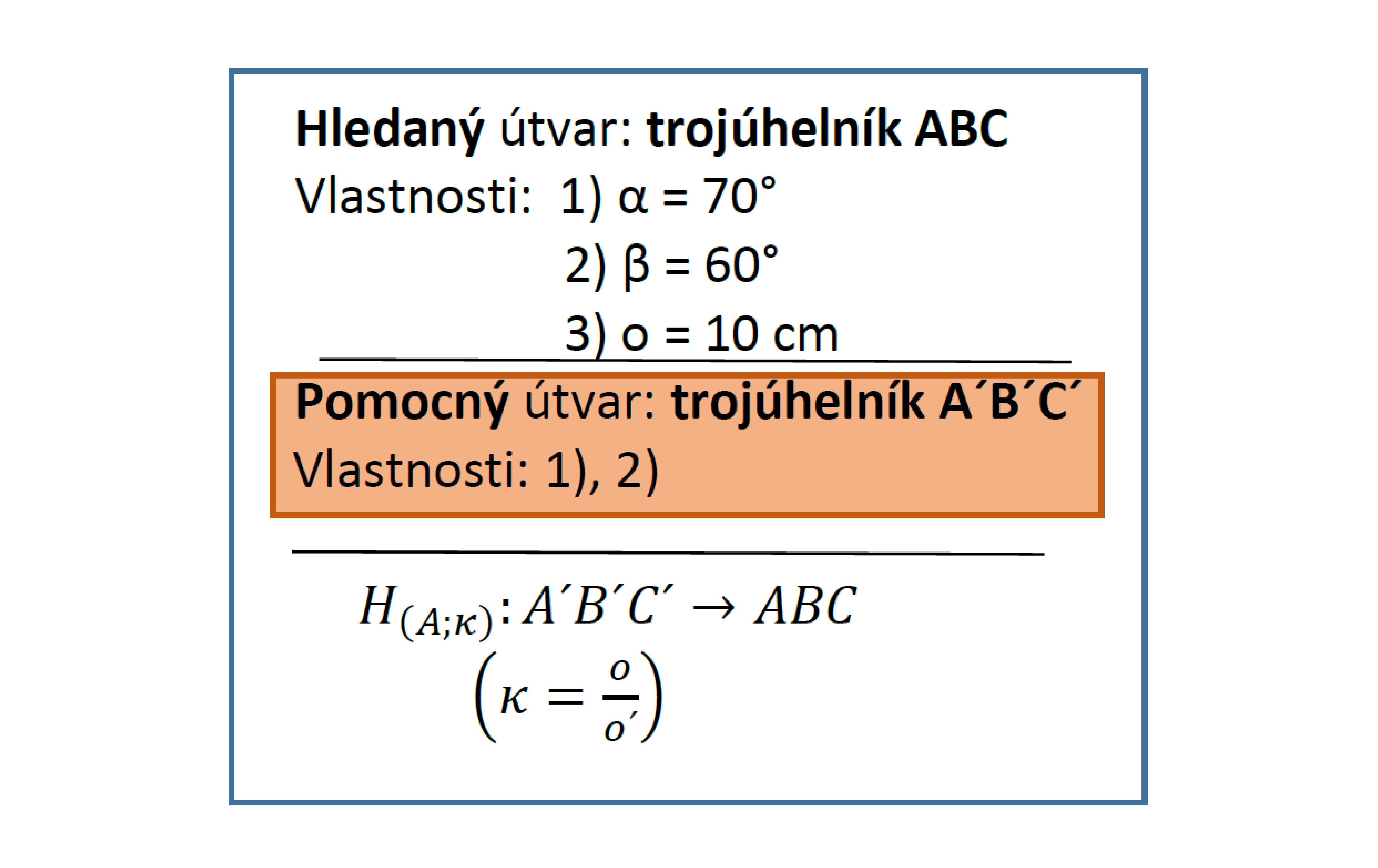
Sestrojte $\bigtriangleup ABC$, je-li dáno: $\alpha = 70^\circ$, $\beta = 60^\circ$, $o = a+b+c = 10\,cm$.
Náčrt:
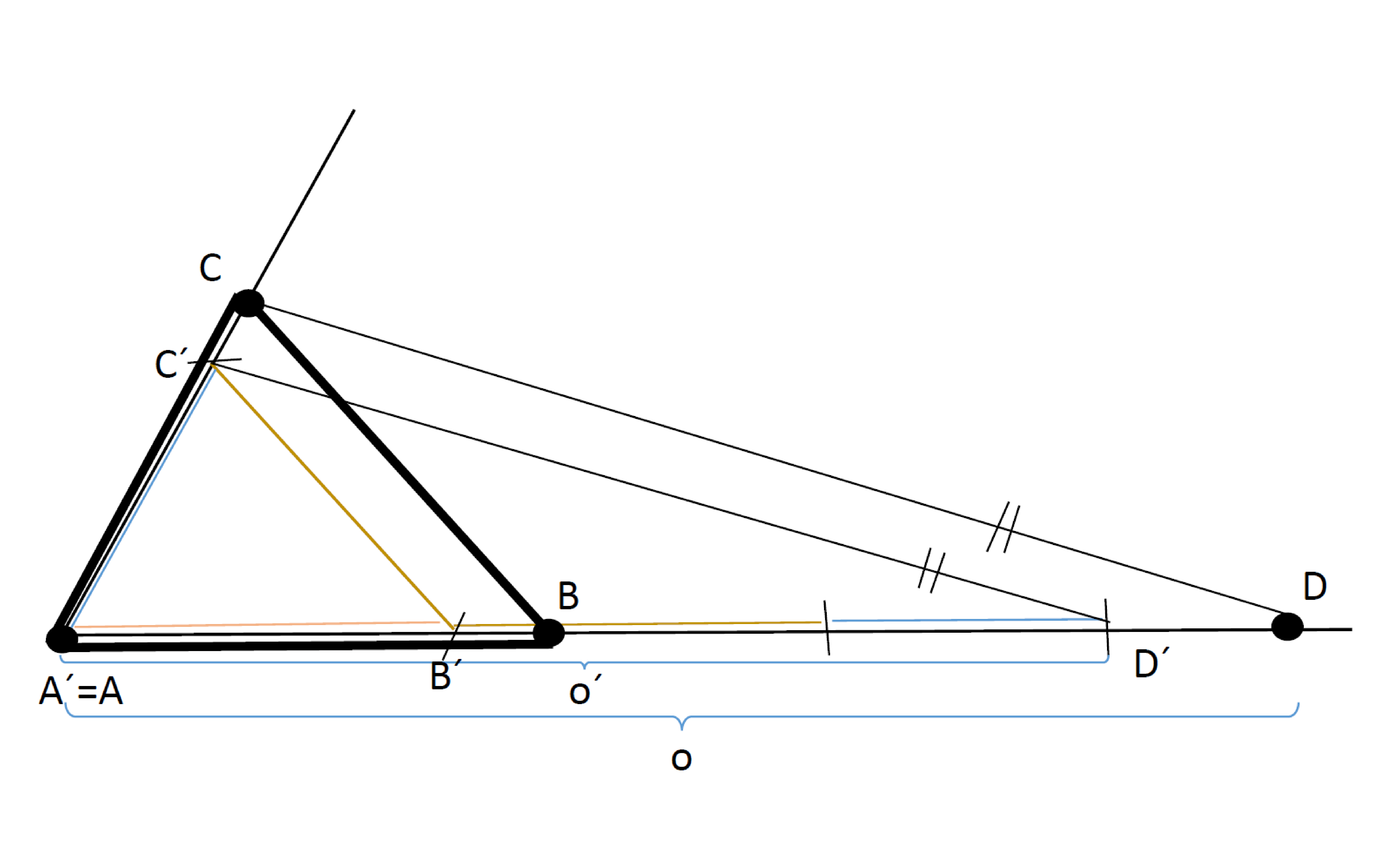
Rozbor:
Úloha 3.3.7
Nechť je dána přímka $t$ a na ní bod $T$, dále nechť je dána kružnice $k$ v jedné z polorovin vyťatých přímkou $t$. Sestrojte kružnici $m$, která se dotýká dané kružnice $k$ a dané přímky $t$ v bodě $T$.
Náčrt:
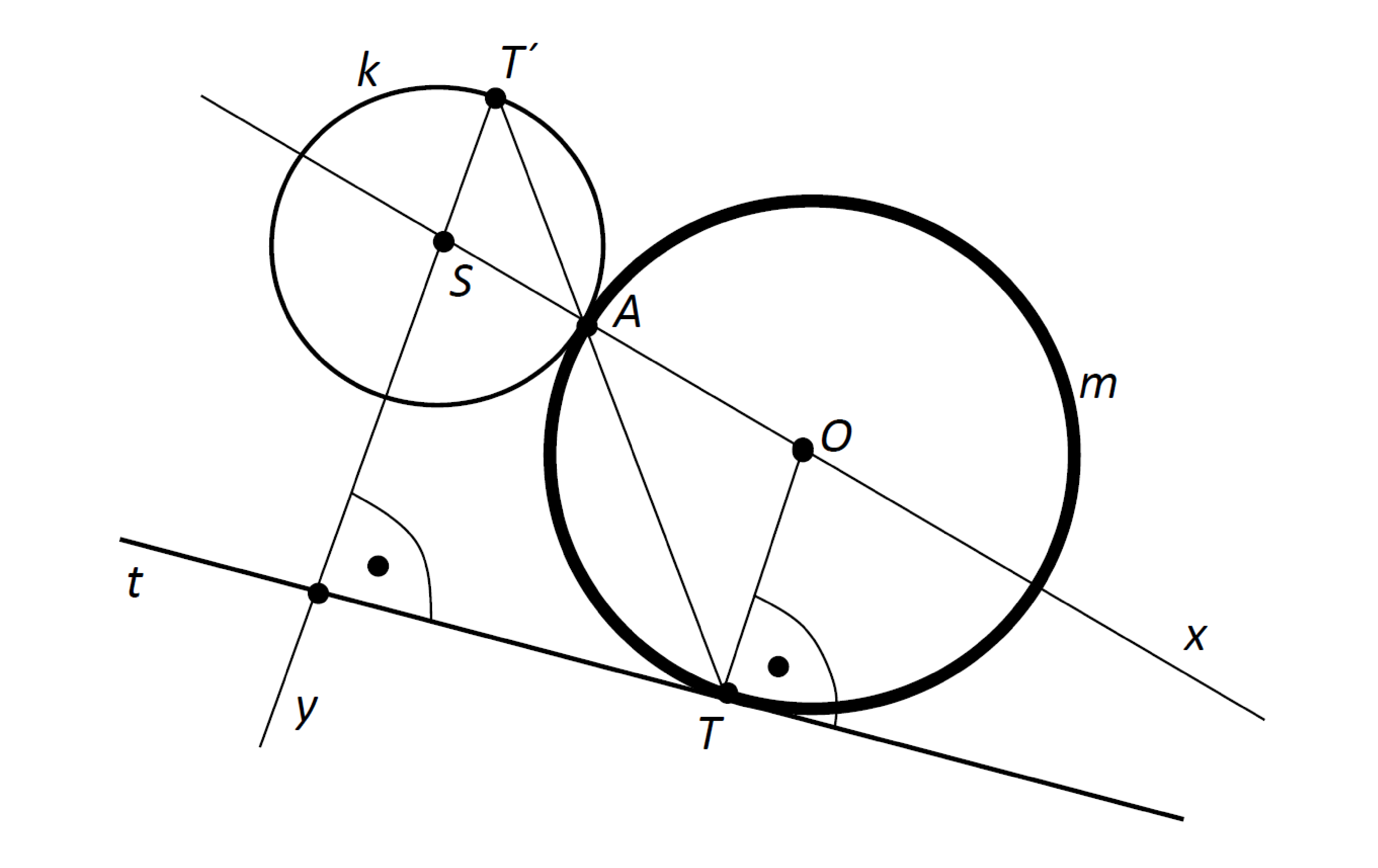
Tato úloha patří rozhodně k náročnějším. Cesta k řešení vede přes podrobný náčrt. Klíčová myšlenka spočívá v tom, že si uvědomíme, že bod dotyku zadané a hledané kružnice představuje jeden ze dvou středů stejnolehlosti těchto kružnic. Pokud v náčrtu nakreslíme správně důležité prvky a vezmeme v úvahu důležité vlastnosti použité stejnolehlosti, řešení bude zřejmé.
Rozbor:
Z náčrtu plyne:
- $A$ – střed stejnolehlosti;
- $O$ leží na kolmici vedené k $t$ bodem $T$
- obrazem $OT$ ve stejnolehlosti se středem v $A$ je $ST'\parallel OT$, tedy $ST'\perp t$
- $A\in k \cap TT'$
- ……
Skutečná výchozí situace:
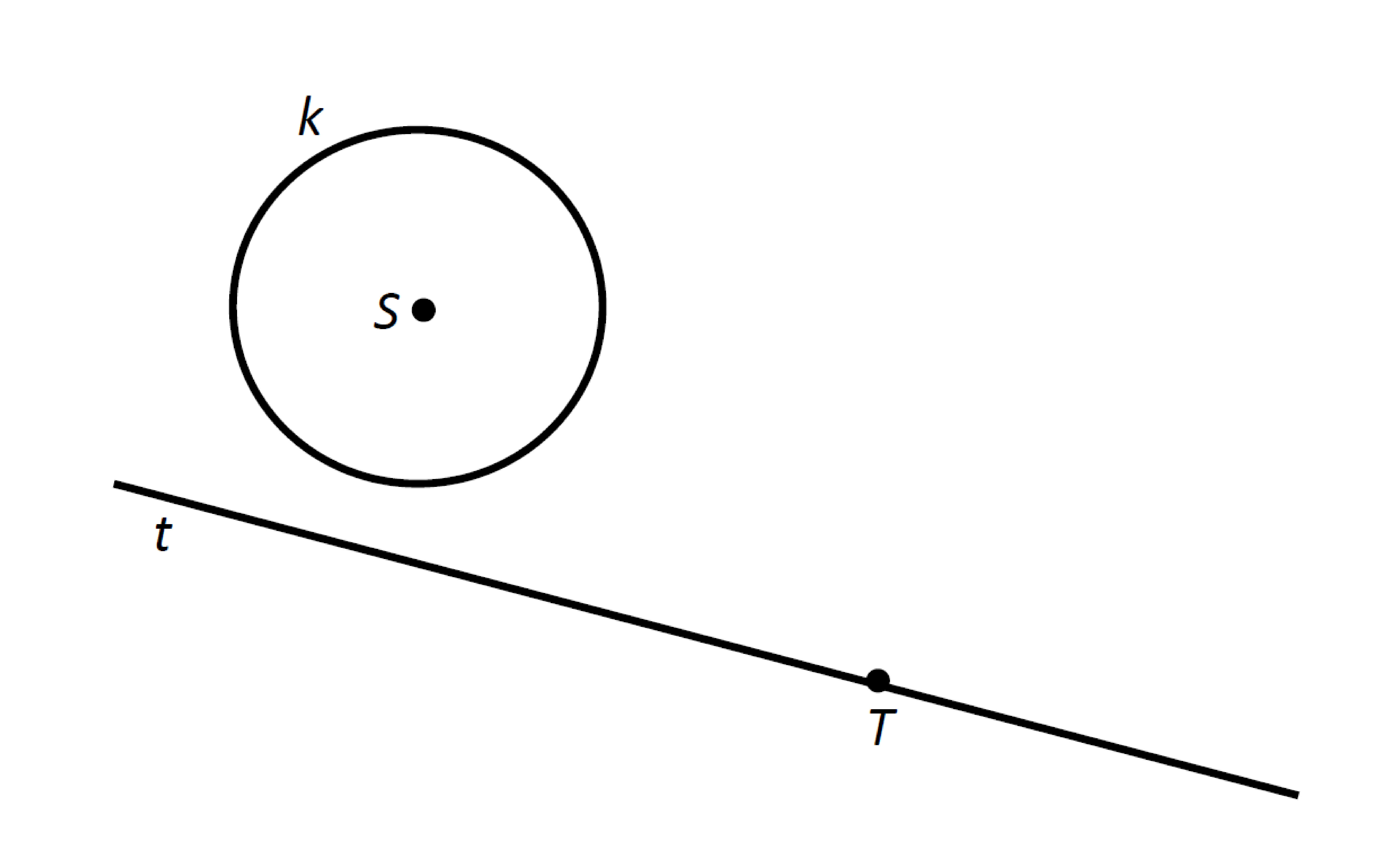
Další úlohy k procvičování
Základní poznatky
Úloha 3.3.8
Je dán obecný trojúhelník $ABC$. Narýsujte:
- $\bigtriangleup A_1B_1C_1$, který je obrazem $\bigtriangleup ABC$ ve stejnolehlosti se středem v bodě $A$ a koeficientem stejnolehlosti $2$.
- $\bigtriangleup A_2B_2C_2$, který je obrazem $\bigtriangleup ABC$ ve stejnolehlosti se středem v bodě $B$ a koeficientem stejnolehlosti $-\frac{1}{2}$.
Jaké jsou poměry podobnosti v těchto zobrazeních?
Úloha 3.3.9
Je dána kružnice $k(S,r=2,5 cm)$ a body $M$ a $N$ s vlastností $M\in k$ a $N$ leží uvnitř kruhu určeného kružnicí $k$. Narýsujte:
- $k_1$, která je obrazem $k$ ve stejnolehlosti se středem v bodě $M$ a koeficientem stejnolehlosti $-\frac{3}{2}$.
- $k_2$, která je obrazem $k$ ve stejnolehlosti se středem v bodě $N$ a koeficientem stejnolehlosti $\frac{1}{2}$.
Úloha 3.3.10
Sestrojte úsečku délky:
- $x=\frac{a\cdot b}{c}$ ($a, b, c$…zadáno)
- $x=\frac{a}{b}$ ($a, b,$ jednotková úsečka …zadáno)
- $x=\frac{\sqrt{a^2+b^2}-c}{d}$ (Volte délky úseček např. $a=6\,cm,b=2\,cm,c=4\,cm,d=3\,cm$).
Typové příklady standardní náročnosti
Úloha 3.3.11
Je dán dutý úhel $\sphericalangle AVB$ a jeho vnitřní bod $P$. Veďte bodem $P$ přímku $p$ tak, aby vytínala na ramenech tohoto úhlu úseky, jejichž délky jsou v poměru $3:4$.
Úloha 3.3.12
Je dán úhel $\sphericalangle AVB$ velikosti $60^\circ$. Uvnitř tohoto úhlu sestrojte bod $M$ tak, aby jeho vzdálenost od vrcholu $V$ byla $d = 5 cm$ a jeho vzdálenosti od ramen $\mapsto VB$ a $\mapsto VA$ byly v poměru $3:4$.
Úloha 3.3.13
Je dána kružnice $k(S;r)$. Narýsujte v ní dva libovolné poloměry a sestrojte tětivu kružnice $k$ tak, aby byla oběma poloměry rozdělena na tři stejné díly.
Úloha 3.3.14
Je dán ostrý úhel $\sphericalangle AVB$ a jeho vnitřní bod $M$. Sestrojte lomenou čáru $MXY$ tak, aby bod $X$ ležel uvnitř polopřímky $\mapsto VA$ , bod $Y$ uvnitř polopřímky $\mapsto VB$ a aby platily tyto vztahy: $XY\perp VB$, $\left\lvert XY\right\rvert = 2\left\lvert MX\right\rvert $.
Úloha 3.3.15
Kruhové výseči vepište obdélník, jehož rozměry jsou v poměru $2:3$.
Úloha 3.3.16
Sestrojte čtverec, je-li dán součet $u+a$ jeho úhlopříčky a strany.