Kombinatorika, pravděpodobnost, statistika
Obsah oddílu
Pravděpodobnost a statistika
Stručný přehled teorie
Pravděpodobnost
Náhodný pokus – pokus, jehož výsledek záleží i při dodržení předem stanovených podmínek na náhodě.
$\Omega = \{\omega_1; \omega_2; ...; \omega_n\}$ … množina všech možných výsledků náhodného pokusu.
Náhodný jev A je podmnožinou množiny $\Omega$ $\dots$ $A \subseteq \Omega$







Úloha 6.2.1
Jaká je pravděpodobnost, že při hodu mincí padne
- rub,
- líc?

Úloha 6.2.2
Jaká je pravděpodobnost, že při hodu hrací kostkou padne
- šestka,
- sudé číslo,
- číslo větší než jedna,
- číslo deset?

Úloha 6.2.3
Hodíme dvěma kostkami, červenou a modrou. Jaká je pravděpodobnost, že
- na obou kostkách padne šestka,
- na obou kostkách padne liché číslo,
- alespoň na jedné kostce padne liché číslo,
- bude součet bodů na kostkách 5,
- bude součet bodů na kostkách menší než 5?

Úloha 6.2.4
Hodíme dvěma kostkami, červenou a modrou. Jaká je pravděpodobnost, že
- padne právě jedna šestka,
- nepadne ani jedna šestka,
- padne aspoň jedna šestka,
- padne nejvýš jedna šestka?

Úloha 6.2.5
Hodíme jedenkrát čtyřmi mincemi najednou. S jakou pravděpodobností padne na dvou mincích líc a na dvou mincích rub?

Úloha 6.2.6
- Jaká je pravděpodobnost, že při třech hodech jednou mincí padne aspoň dvakrát líc?
- Jaká je pravděpodobnost, že při jednom hodu třemi mincemi najednou padne aspoň na dvou líc?

Úloha 6.2.7
Šest studentek a osm studentů, mezi kterými jsou Anna a Pavel, mají ze svého středu vylosovat čtyřčlennou skupinu. Jaká je pravděpodobnost, že mezi vylosovanými studenty bude
- Anna i Pavel;
- Pavel;
- Anna nebo Pavel;
- Anna, ale Pavel ne?

Úloha 6.2.8
Mezi 20 studenty je 6 aktivních sportovců. Jaká je pravděpodobnost, že při náhodném výběru čtyř studentů budou mezi nimi právě dva sportovci?

Úloha 6.2.9
V osudí je 15 kuliček, z nich 6 je bílých, ostatní jsou modré. Určete pravděpodobnost, že při náhodném výběru 5 kuliček z osudí budou mezi nimi alespoň dvě bílé.

Úloha 6.2.10
Hodíme třikrát kostkou. Vypočítejte pravděpodobnost, že při prvním hodu padne sudé číslo, při druhém hodu padne číslo větší než 3 a při třetím hodu padne šestka.
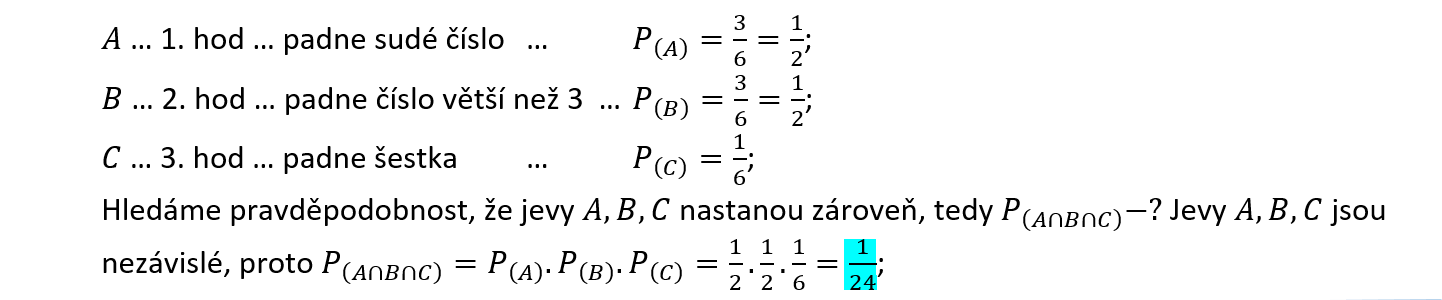
Úloha 6.2.11
Žárovka svítí se spolehlivostí 92 %. Jestliže zapojíme dvě žárovky sériově, jaká je pravděpodobnost, že
- budou svítit,
- nebudou svítit?


Úloha 6.2.12
Žárovka svítí se spolehlivostí 92 %. Jestliže zapojíme dvě žárovky paralelně, jaká je pravděpodobnost, že
- budou svítit obě,
- bude svítit aspoň jedna,
- aspoň jedna svítit nebude,
- nebude svítit žádná?
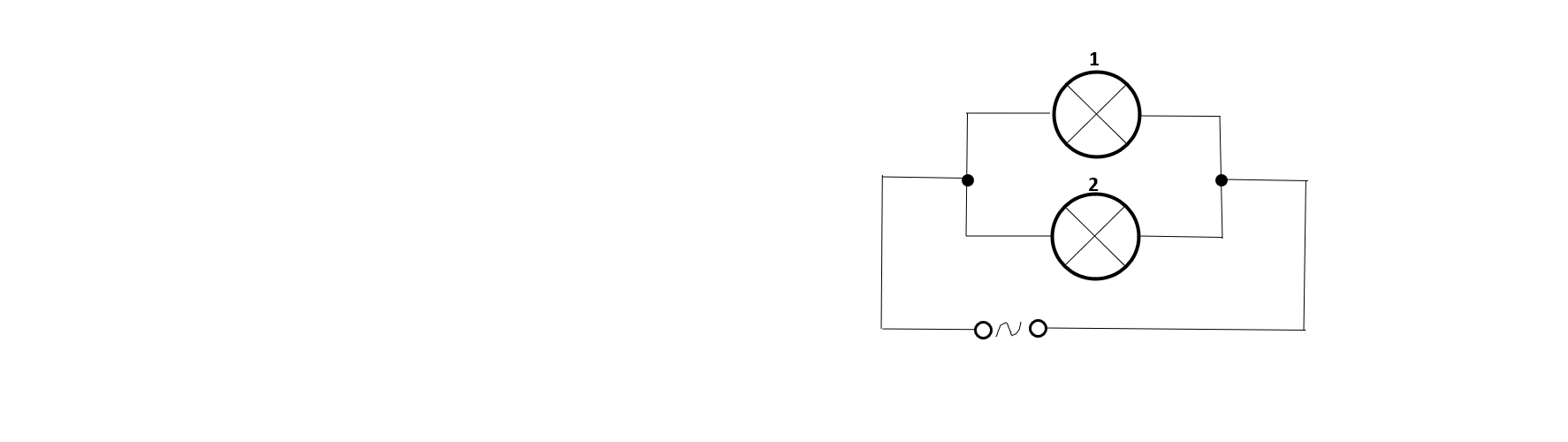

Úloha 6.2.13
Pravděpodobnost, že je žárovka v pořádku, je pro všechny žárovky $p_1=p_2=p_3=p=0,8$. Jaká je pravděpodobnost, že
- všechny žárovky svítí?
- aspoň jedna žárovka nesvítí?
- obvodem prochází proud?


Úloha 6.2.14
Dva střelci střílejí nezávisle na sobě na cíl. První střelec zasáhne s cíl pravděpodobností $p_1=0,8$ druhý s pravděpodobností $p_2=0,6$. Jaká je pravděpodobnost, že
- prvním výstřelem alespoň jeden zasáhne cíl,
- prvním výstřelem právě jeden zasáhne cíl,
- prvním výstřelem žádný z nich nezasáhne cíl,
- z prvních pěti výstřelů první střelec zasáhne cíl právě čtyřikrát,
- z prvních pěti výstřelů první střelec zasáhne cíl aspoň čtyřikrát.

Úloha 6.2.15
Zjistilo se, že pravděpodobnost dodávky, v níž je víc než 2 % vadných výrobků, je 0,08. Určete pravděpodobnost, že mezi 20 dodávkami budou právě tři s více než 2 % vadných výrobků.

Úloha 6.2.16
Kolikrát musíme hodit dvěma kostkami, aby dvojice šestek padla s pravděpodobností větší než 80 %?
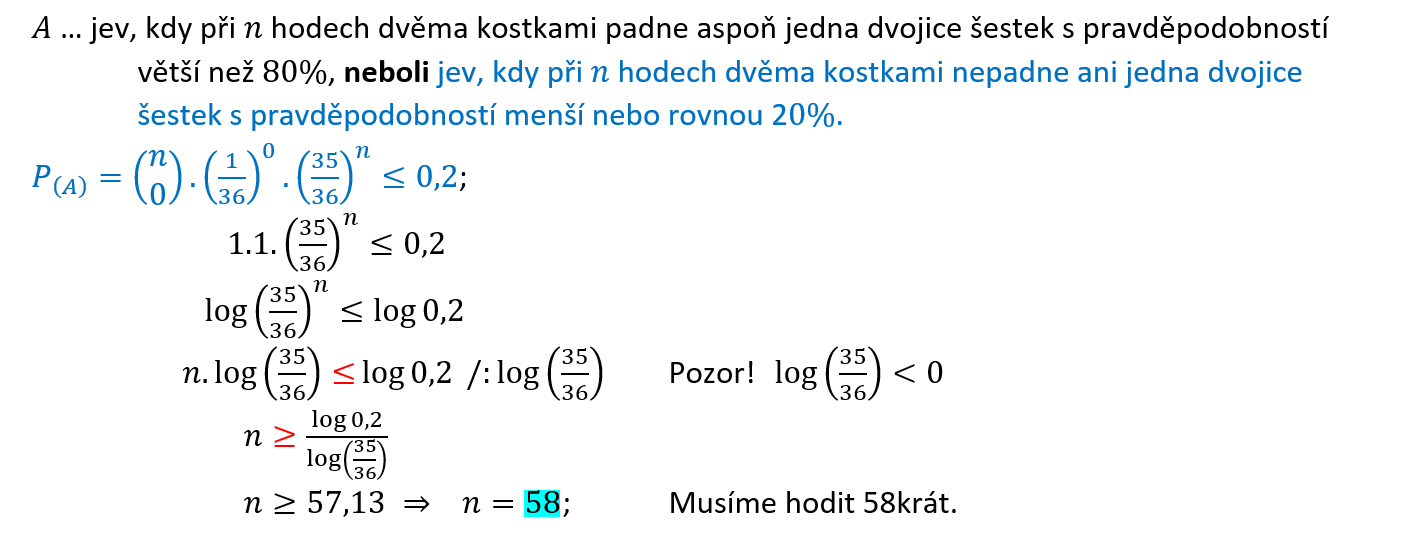
Úloha 6.2.17
V osudí je 8 červených a 6 bílých koulí.
- Vytáhneme postupně tři koule. Po každém tahu kouli vracíme. Jaká je pravděpodobnost, že postupně vytáhneme kouli červenou, bílou, červenou?
- Vytáhneme postupně tři koule. Po každém tahu kouli nevracíme. Jaká je pravděpodobnost, že postupně vytáhneme kouli červenou, bílou, červenou?
- Vytáhneme tři koule najednou. S jakou pravděpodobností jsou ve vytažené trojici dvě koule červené a jedna koule bílá?

Úloha 6.2.18
Dlouhodobým pozorováním bylo zjištěno, že pravděpodobnost narození chlapce je 0,485, pravděpodobnost narození děvčete je 0,515. Jaká je pravděpodobnost, že rodina, která má tři děti, má
- právě tři děvčata,
- alespoň jednoho chlapce,
- dva chlapce a jedno děvče,
- alespoň jednu dívku?

Úloha 6.2.19
V loterii vyhrává 4. cenu ten, jehož výrobní číslo losu končí stejným dvojčíslím, jako je dvojčíslí, které bylo vylosováno. S jakou pravděpodobností vyhrajeme aspoň jednu 4. cenu, koupíme-li si
- jeden los,
- pět losů?
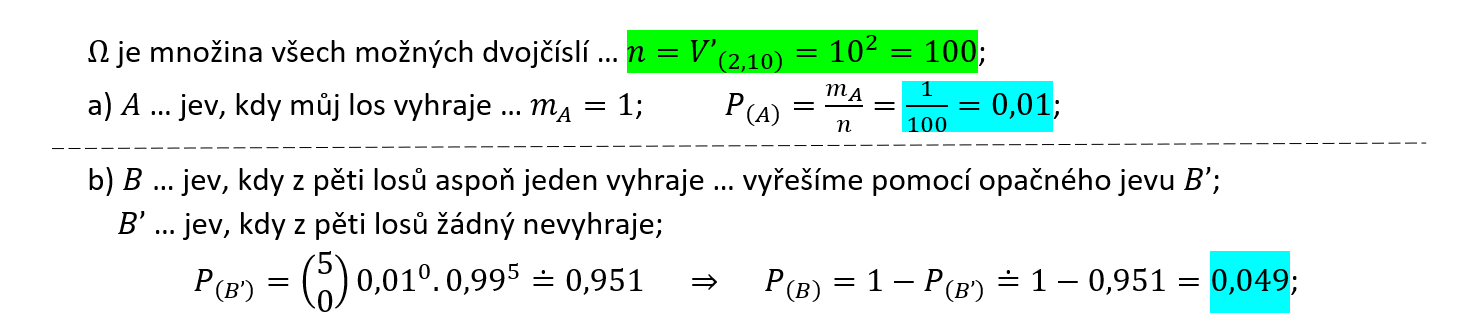
Úloha 6.2.20
Student dostal test, který obsahuje 10 otázek. Ke každé otázce vybírá právě jednu odpověď z možností a, b, c, d. Jaká je pravděpodobnost, že student odpoví aspoň 70 % otázek správně, volí-li odpovědi zcela náhodně?
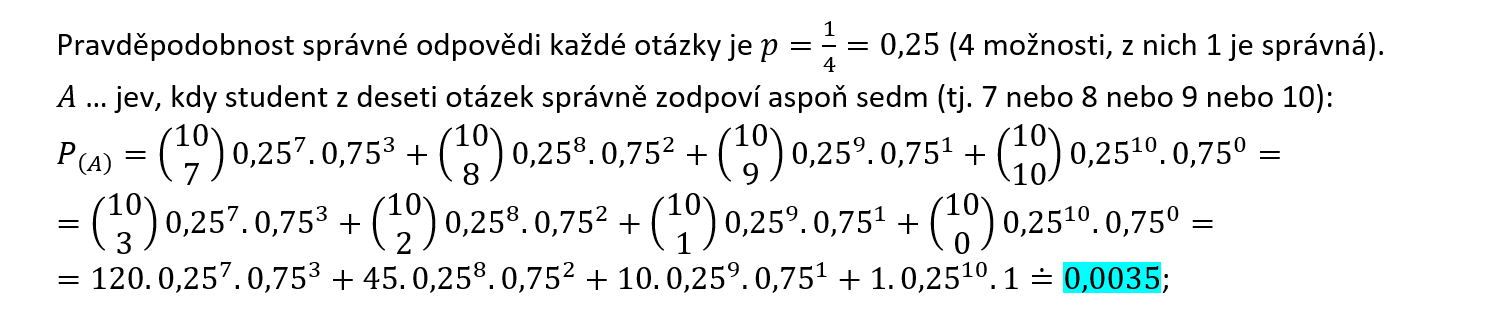
Základy statistiky
Úloha 6.2.21
V souboru A byl sledován údaj o počtu dětí ve 13 rodinách. Vypočítejte aritmetický průměr, modus a medián.

Úloha 6.2.22
V souboru B byl sledován údaj o počtu dětí ve 14 rodinách. Vypočítejte aritmetický průměr, modus a medián.

Úloha 6.2.23
Ačkoliv se počet zaměstnanců prosperujícího výrobního závodu během let neměnil, díky zavádění nových technologií rostl počet výrobků $x_i$ připadajících na jednoho zaměstnance za rok tak, jak to ukazuje následující tabulka.
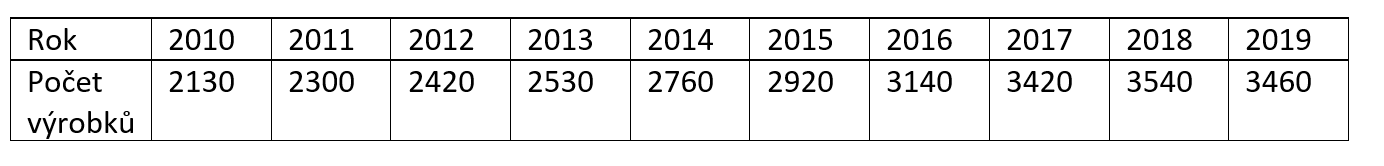
- Doplňte do tabulky řádek s ročními přírůstky $y_i=x_i-x_{i-1}$ a zjistěte, ve kterém roce vzrostl počet výrobků na jednoho zaměstnance nejvíce.
- Určete průměrný přírůstek $\overline{y}$ počtu výrobků mezi lety 2010 až 2019.
- Doplňte do tabulky řádek s ročními tempy růstu $z_i=\frac{\displaystyle x_i}{\displaystyle x_{i-1}}$ a zjistěte, ve kterém roce rostl počet výrobků nejrychleji.
- Určete průměrné tempo růstu počtu výrobků $\overline{z_G}= \sqrt[n]{z_1\cdot z_2 \cdot \dots \cdot z_n}$ mezi lety 2010 až 2019.

Úloha 6.2.24
Na meteorologické stanici měřili každou hodinu teplotu vzduchu během jarního dne. Naměřené hodnoty byly: 8°C, 7°C, 7°C, 6°C, 6°C, 6°C, 6°C, 8°C, 10°C, 12°C, 14°C, 16°C, 16°C, 16°C, 16°C, 15°C, 15°C, 14°C.
Hodinová měření byla znovu provedena během dne uprostřed léta s těmito naměřenými hodnotami:12°C, 12°C, 11°C, 11°C, 14°C, 15°C, 20°C, 24°C, 28°C, 30°C, 32°C, 32°C, 34°C, 37°C, 36°C, 30°C, 28°C, 26°C. Určete pro obě skupiny variační rozpětí a srovnejte variabilitu obou skupin dat.

Úloha 6.2.25
Bertillonáž je již nepoužívaná metoda identifikace osob pomocí tělesných rozměrů. Byl o ní natočen jeden z dílů úspěšného televizního seriálu Dobrodružství kriminalistiky. Pět studentů se touto metodou inspirovalo a změřilo délku části své paže od lokte po konečky prstů (viz tabulka). Vypočítejte průměrnou absolutní odchylku $\bar{d}$ a relativní odchylku r tohoto měření.


Úloha 6.2.26
V rámci laboratorní práce z fyziky dostali studenti za úkol změřit tloušťku skleněné desky. Následující tabulka obsahuje výsledky deseti provedených měření. Vypočítejte rozptyl, směrodatnou odchylku měření a variační koeficient.
Pozn.: Tato úloha představuje základní zpracování výsledků měření v laboratorních cvičeních – studenti je buď už znají z fyziky, nebo je zanedlouho ve fyzice využijí.


Úloha 6.2.27
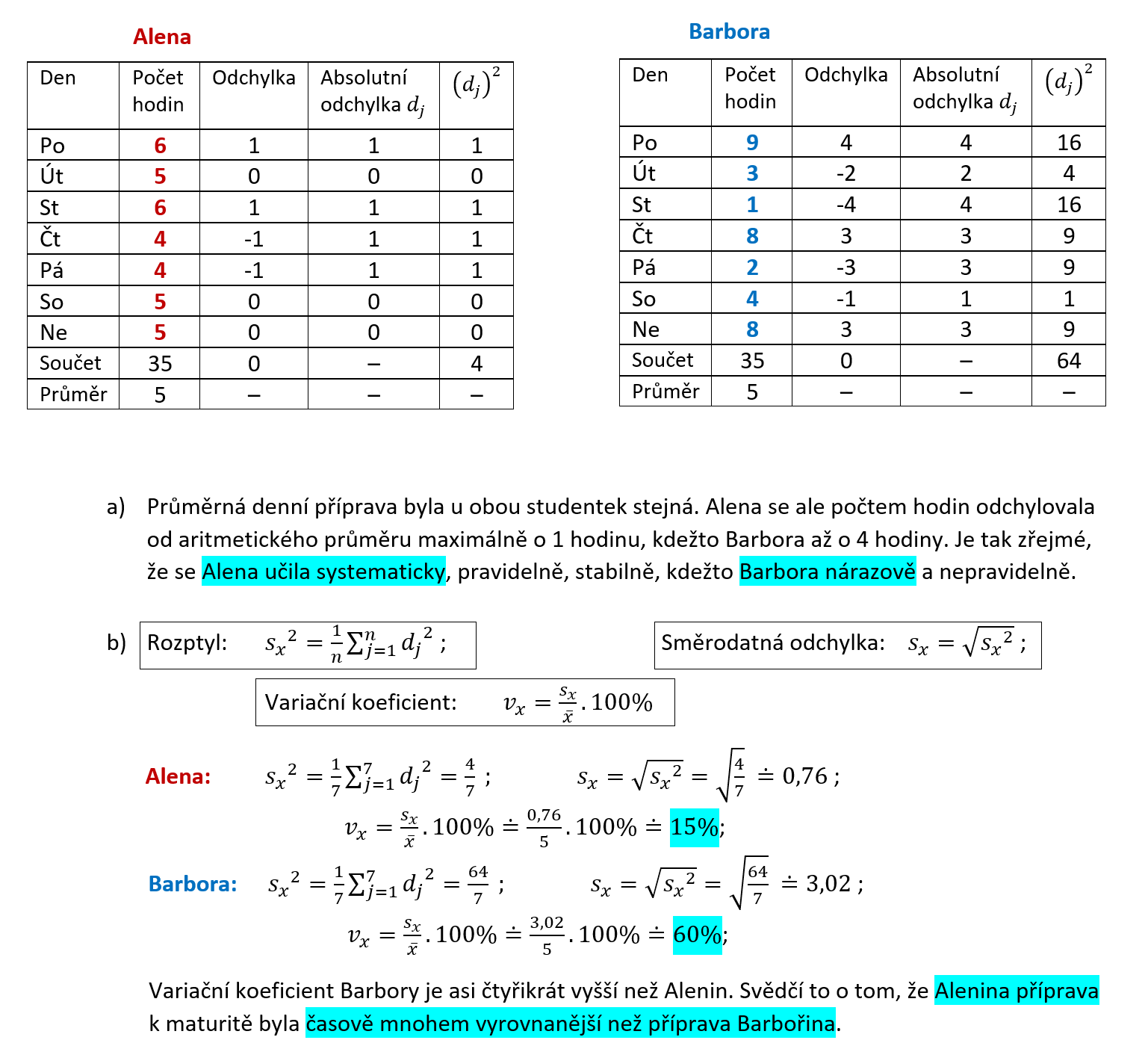
Alena a Barbora se učily na maturitu. Počet hodin, které strávily během týdne učením, je následující:
Alena: 6; 5; 6; 4; 4; 5; 5;
Barbora: 4; 3; 1; 8; 2; 9; 8.
- Vypočítejte absolutní odchylky počtu hodin strávených studiem a z vypočítaných údajů vyvoďte závěr týkající se způsobu přípravy obou studentek na maturitu.
- Vypočítejte také variační koeficienty pro oba soubory dat, a využijte jejich srovnání pro potvrzení závěru o způsobu přípravy k maturitě.
Úloha 6.2.28
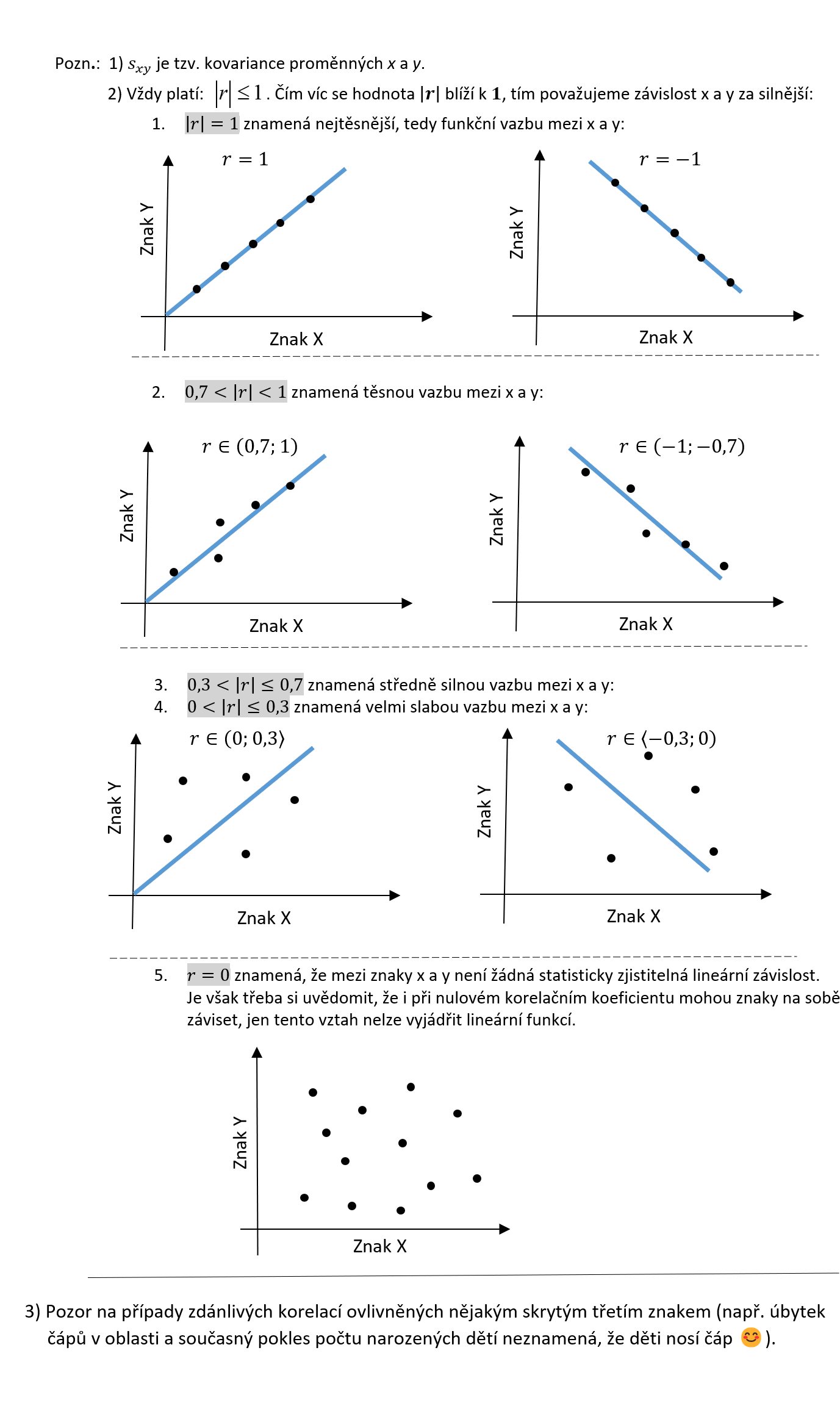
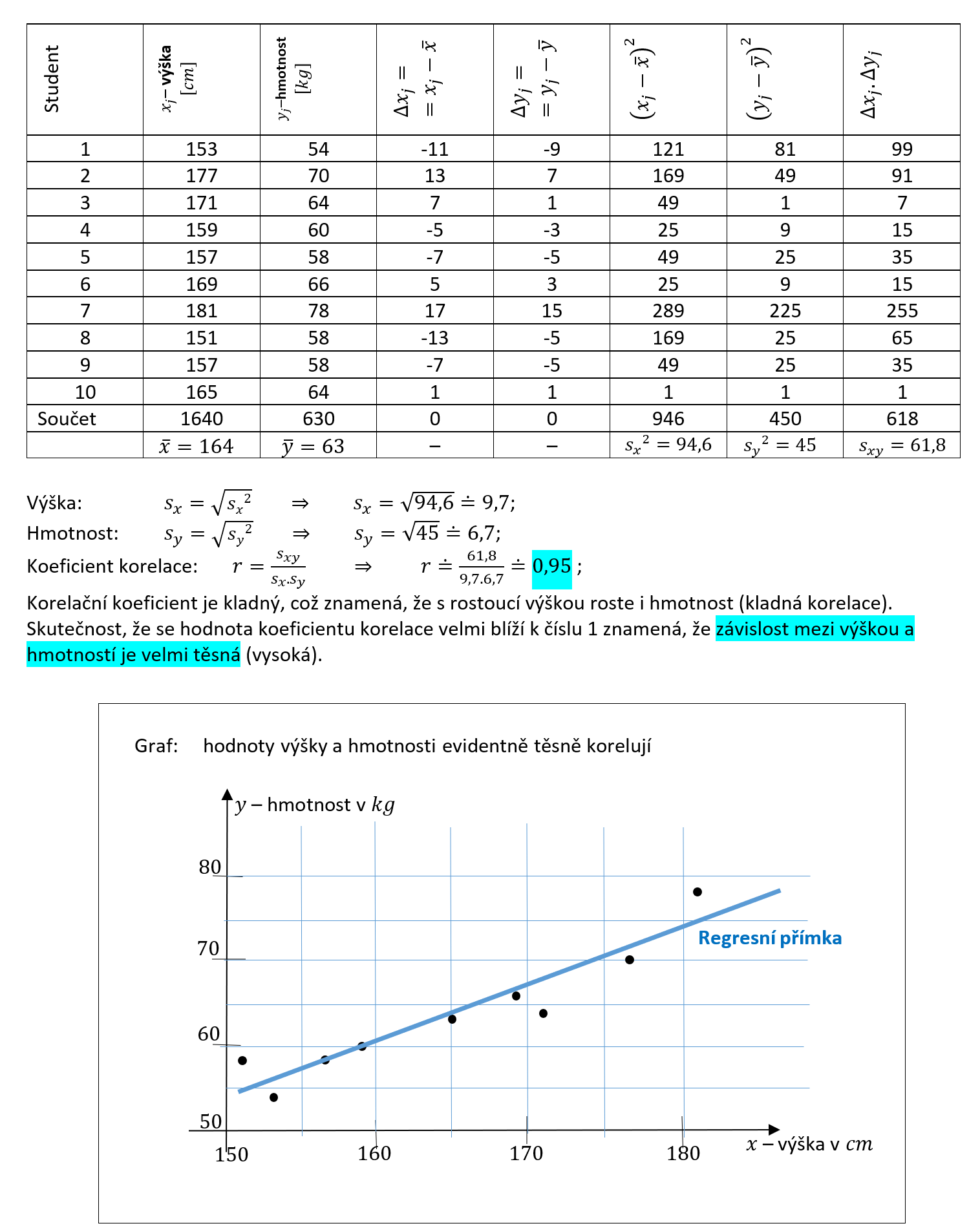
Vyhodnoťte závislost výšky a hmotnosti u deseti studentů – viz tabulka:
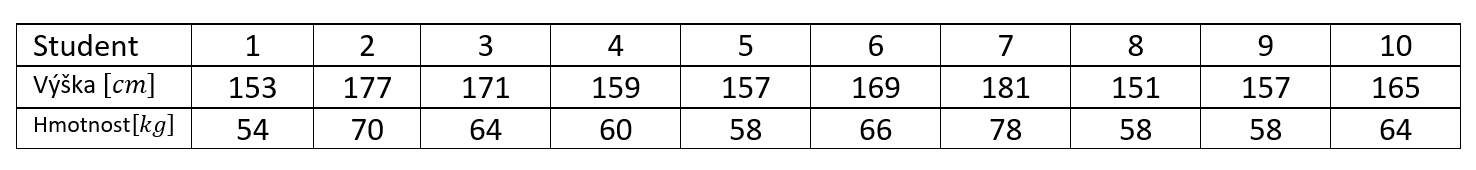
Základní poznatky
Úloha 6.2.29
Jaká je pravděpodobnost, že při hodu třemi kostkami padne součet 12?
0,116
Úloha 6.2.30
55 % populace tvoří ženy, 45 % muži. Určitou chorobou trpí 1 % žen a 5% mužů. Jaká je p., že náhodně vybraná osoba z populace trpí touto chorobou?
0,028
Úloha 6.2.31
Dvanáct studentů, mezi kterými je Pavel a Tomáš, mají ze svého středu vylosovat 4-člennou skupinu. Jaká je pravděpodobnost, že ve skupině bude:
- Tomáš
- Tomáš, ale Pavel ne
- Tomáš a Pavel
- Tomáš nebo Pavel
- 0,333
- 0,242
- 0,091
- 0,576
Úloha 6.2.32
Jaká je pravděpodobnost, že se Jana a Tomáš narodili ve stejný měsíc?
(Počítejte, že 1 měsíc je 1/12 roku)
0,0833
Úloha 6.2.33
Státní maturita 2017
Z 25 žáků jedné třídy domácí úkol 3 žáci nevypracovali, 6 žáků vypracovalo chybně a zbývající žáci jej vypracovali správně.
Učitel náhodně vybral dvojici žáků.
Jaká je pravděpodobnost, že oba žáci budou mít úkol vypracován správně?
2/5
Úloha 6.2.34
Státní maturita 2015
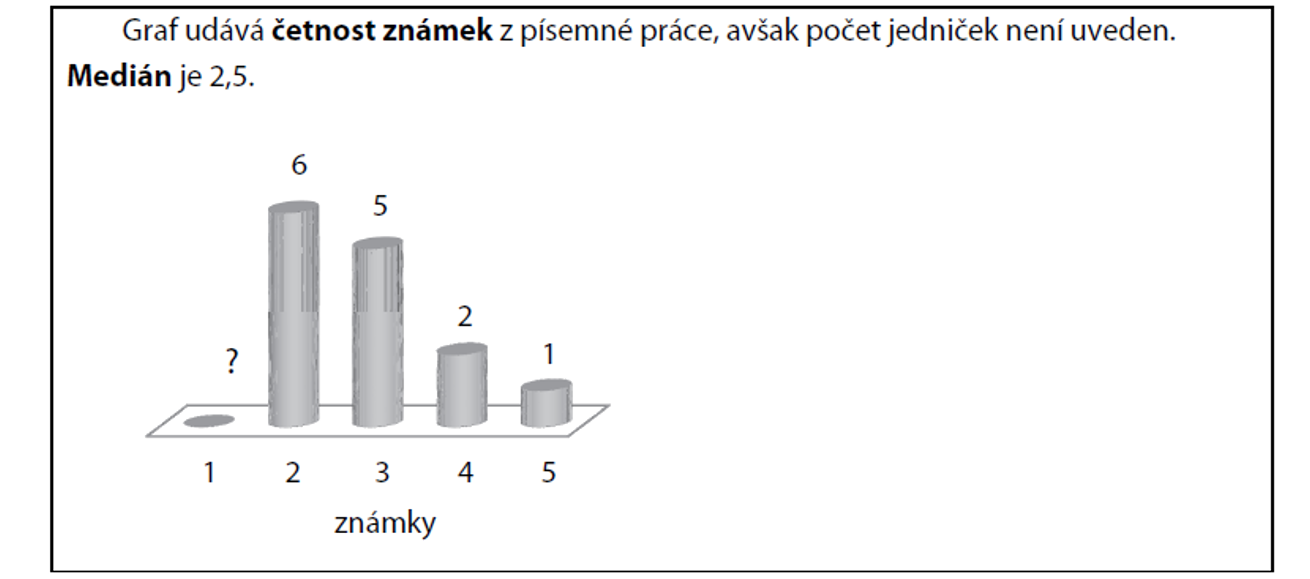
Kolik písemných prací bylo oznámkováno?
16
Typové příklady standardní náročnosti
Úloha 6.2.35
Z 10 studentů, mezi nimiž jsou Adam a Petr vybíráme tříčlennou komisi. Jaká je pravděpodobnost, že Adam nebo Petr budou mezi nimi?
8/15
Úloha 6.2.36
Hodíme 3-krát kostkou. Jaká je pravděpodobnost, že při 1. hodu nebo při 2. nebo při 3. padne sudé číslo?
7/8
Úloha 6.2.37
Každý ze spínačů je náhodně v poloze zapnuto nebo vypnuto nezávisle na druhých. Jaká je pravděpodobnost, že součástkou bude protékat el. proud?

15/64
Úloha 6.2.38
Žárovka svítí se spolehlivostí 85 %. Jaká je spolehlivost systému (alespoň část svítí), jsou-li zapojeny:
- dvě žárovky sériově,
- dvě žárovky paralelně,
- dvě žárovky sériově a třetí k nim paralelně
- 0,723
- 0,978
- 0,958
Úloha 6.2.39
Test obsahuje 10 otázek, čtyři možné odpovědi, z nichž jedna je správná. Jaká je pravděpodobnost, že náhodným volením odpovědí vybereme alespoň 5 správných?
0,078
Úloha 6.2.40
Lék úspěšně léčí 90 % případů onemocnění. Vypočítejte pravděpodobnost, že vyléčí alespoň 18 pacientů z 20, kterým je lék podán.
0,677
Úloha 6.2.41
Tabulka zaznamenává známky z matematiky pro 16 testů. Vypočítejte:
- Relativní četnost známky 2.
- Modus a medián známek z testu.
- Aritmetický průměr známek z testu.
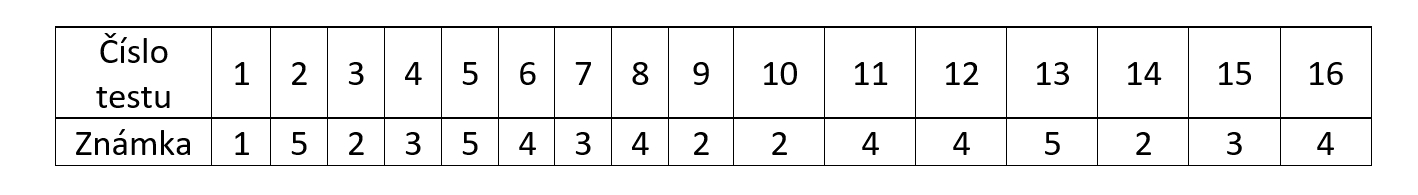
- 25%
- modus 4, medián 3,5,
- 53/16
Úloha 6.2.42
Průměrná cena 1 kg jablek je 27 Kč, průměrná cena 1 kg hrušek je 30 Kč. Nakoupili jsme jablka, hrušky a pomeranče. Čtvrtinu nakoupeného množství tvořily jablka, třetinu hrušky a zbytek tvořily pomeranče. Jaká je průměrná cena 1 kg pomerančů, jestliže byla průměrná cena 1 kg smíšeného zboží 32 Kč?
39,6 Kč
Rozšiřující cvičení
Úloha 6.2.43
Státní maturita Matematika+ 2017

A, N, A