Hypergeometrické rozdělení: $Hg(N,M,n)$
Uvažujme množinu $N$ prvků, mezi kterými je $M$ prvků se sledovanou vlastností. Náhodně vybereme $n$ prvků bez vracení ze všech $N$ prvků. Náhodná veličina $X \sim Hg(N,M,n)$ udává počet prvků se sledovanou vlastností v náhodném výběru $n$ prvků, přičemž $M\in\mathbb{N}$, $N \in \mathbb{N}$, $1\leq n \lt N$, $1\leq M \lt N$.
Pravděpodobnostní funkce je tvaru:
\begin{equation}
p(x) =
\begin{cases}
\frac{\binom{M}{x} \binom{N-M}{n-x}}{\binom{N}{n}} &\text{pro $x=max\{0,M-N+n\}, …, min\{n,M\} $}\\
0 &\text{jinak}\tag{1.20}
\end{cases}
\end{equation}
Distribuční funkce je tvaru:
\[F(x) = \sum_{x_i \leq x} \frac{\binom{M}{x_i} \binom{N-M}{n-x_i}}{\binom{N}{n}}\]
Vztahy pro střední hodnotu a rozptyl:
\begin{align}
E(X) &= n\frac{M}{N}\tag{1.21} \\
D(X) &= n\frac{M}{N}\biggl(1-\frac{M}{N}\biggr)\frac{N-n}{N-1}\tag{1.22}
\end{align}
Limitním případem hypergeometrického rozdělení je rozdělení binomické, pro $x \rightarrow \infty$ a $\frac{M}{N} \rightarrow 0$ je $Hg(N,M,n) \approx Bi(n,p=\frac{M}{N})$. Ztrácí se totiž rozdíl mezi výběrem s vracením a výběrem bez vracení.
Software STATISTICA používá pro výpočet pravděpodobnostní funkce funkci $Hypergeometric(x;M;N;n)$ a pro výpočet distribuční funkce funkci $IHypergeometric(x;M;N;n)$, kde:
$x$ = počet prvků se sledovanou vlastností,
$M$ = počet všech označených prvků,
$N$ = počet všech prvků,
$n$ = rozsah výběru z $N$ prvků.
Příklad 1.7:
V bance mají seznam 50 žadatelů o úvěr. Mezi nimi je 35 spolehlivých a 15 nespolehlivých žadatelů. Určete pravděpodobnost, že jestli banka poskytne úvěr právě 20 žádatelům, bude z nich 15 spolehlivých a 5 nespolehlivých.
postup
postup v programu Statistica
Jedná se o hypergeometrické rozdělení pravděpodobnosti s parametry:
N = 150 … všichni žadatelé
M = 35 … spolehliví žadatelé
N-M = 15 … nespolehliví žadatelé
n = 20 … počet poskytnutých úvěrů
x = 15 … vybraní spolehliví zájemci
n-x = 5 … vybraní nespolehliví zájemci
Pak námi hledaná pravděpodobnost je:
$P(A) = \frac{\binom{35}{15}\binom{15}{5}}{\binom{50}{20}} = 0,20695$
Pravděpodobnost, že z 20-ti poskytnutých úvěrů bude 15 poskytnutých spolehlivým žadatelům a 5 nespolehlivým žadatelům, je 20,7 %.
1. způsob: vytvoříme nový datový soubor o 1 proměnné a 1 případu a do dlouhého jména proměnné napíšeme:
$=Hypergeometric(15;35;50;20)$ a dostaneme výsledek 0,20695388.
2. způsob: výpočet pomocí praděpodobnostního kalkulátoru: v menu vybereme: Statistiky - Kalkulátor - Rozdělení: Hypergeometrické - $M$ - napíšeme 35, $N$ - napíšeme 50, $n$ - napíšeme 20, $X$ - napíšeme 15 - Pravděp., v okénku $p$ se objeví vypočtená pravděpodobnost: 0,206954.
Příklad 1.8:
Mezi 15 vejci je v jisté prodejně 6 prasklých. Jaká je pravděpodobnost, že když vybereme 4 vejce, budou z nich:
- právě 2 prasklá,
- alespoň 2 prasklá.
postup
postup v programu Statistica
Náhodná veličina $X$ udává počet vybraných prasklých vajec, $X \sim Hg(15,6,4)$.
- $P(X=2) = \frac{\binom{6}{2}\binom{9}{2}}{\binom{15}{4}} = \frac{540}{1365} = 0,3956$
Pravděpodobnost, že mezi 4 vybranými vejci budou právě 2 prasklá, je 39,56 %.
- $P(X \geq 2) = 1-P(X\leq 1) = 1-F(1) = 1-\sum_{x_i=0}^1 \frac{\binom{6}{x_i} \binom{9}{4-x_i}}{\binom{15}{4}} =\\ = 1-0,4615 = 0,5385$
Pravděpodobnost, že mezi 4 vybranými vejci budou alespoň 2 prasklá, je 53,85 %.
1. způsob: vytvoříme nový datový soubor o 2 proměnných a 1 případu. Do dlouhého jména proměnných postupně píšeme:
- $=Hypergeometric(2;6;15;4)$ a dostaneme výsledek 0,3956044.
- $=1-IHypergeometric(1;6;15;4)$ a dostaneme výsledek 0,53846.
2. způsob: výpočet pomocí pravděpodobnostního kalkulátoru: v menu vybereme: Statistiky - Kalkulátor - Rozdělení: Hypergeometrické.
- $M$ - napíšeme 6, $N$ - napíšeme 15, $n$ - napíšeme 4, $X$ - napíšeme 2 - Pravděp., v okénku $p$ se objeví vypočtená pravděpodobnost: 0,395604.
- $M$ - napíšeme 6, $N$ - napíšeme 15, $n$ - napíšeme 4, $X$ - napíšeme 1 - Kum. pravděpodobnost, v okénku $p$ se objeví vypočtená pravděpodobnost: 0,461538, kterou však musíme ještě odečíst od jedničky, takže námi hledaná pravděpodobnost je: 1-0,461538 = 0,538462.
Vykreslení grafu pravděpodobnostní a distribuční funkce náhodné veličiny $X \sim Hg(15,6,4)$ v systému STATISTICA: Vytvoříme nový datový soubor o 3 proměnných a 5 případech. První proměnnou nazveme X a uložíme do ní hodnoty 0 až 4: do dlouhého jména proměnné napíšeme: $=v0-1$. Druhou proměnnou nazveme PF a uložíme do ní hodnoty pravděpodobnostní funkce, do dlouhého jména proměnné napíšeme: $=Hypergeometric(x;6;15;4)$. Třetí proměnnou nazveme DF a uložíme do ní hodnoty distribuční funkce, do dlouhého jména proměnné napíšeme: $=IHypergeometric(x;6;15;4)$.
Pravděpodobnostní funkce: Grafy - Bodové grafy - Proměnné X a PF - OK - odškrtneme Typ proložení: lineární - OK.

Distribuční funkce: Grafy - Bodové grafy - Proměnné X a DF - OK - odškrtneme Typ proložení: lineární - OK - 2krát klikneme na pozadí grafu - Spojnice - Obecné - odškrtneme Značky - zaškrtneme Spojnice - Typ čáry - Schod - OK. Opět dvojklikem na pozadí grafu vybereme: Osa - Měříto - Mód: Ručně - Minimum = 0, Maximum = 4 - OK.
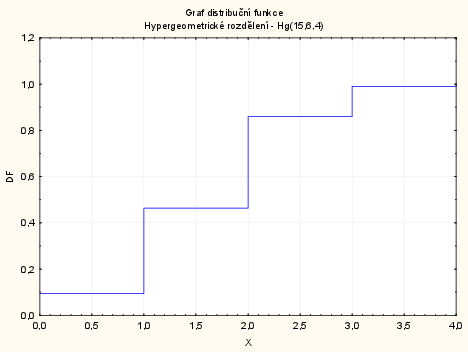
Druhý možný způsob vykreslení grafů pomocí pravděpodobnostního kalkulátoru není možné při hypergeometrickém rozdělení použít, neboť STATISTICA nevykresluje správně graf pravděpodobnostní funkce při jeho použití.



