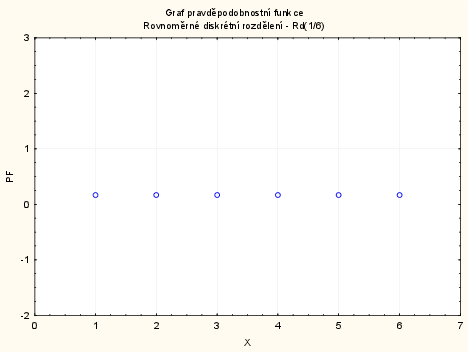
Uvažujme hod kostkou, množina $G$ obsahuje prvky $G=\{1,2,3,4,5,6\}$. Každý výsledek je v tomto případě stejně pravděpodobný. Náhodná veličina $X$ udává hozené číslo, $X \sim Rd(G)$, $p(x) = \frac{1}{6}$.
Vykreslení grafů $X \sim Rd(G)$, kde $G=\{1,2,3,4,5,6\}$ v systému STATISTICA:
Pravděpodobnostní funkce: vytvoříme nový datový soubor o 2 proměnných a 6 případech. První proměnnou nazveme X a uložíme do ní hodnoty 1 až 6: do dlouhého jména proměnné napíšeme: $=v0$. Druhou proměnnou nazveme PF a uložíme do ní hodnoty pravděpodobnostní funkce: $p(x) = \frac{1}{6}$, do dlouhého jména proměnné napíšeme: $= \frac{1}{6}$.
Grafy - Bodové grafy - Proměnné X a PF - OK - odškrtneme Typ proložení: lineární - OK.
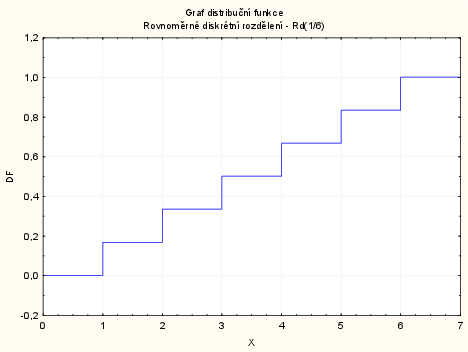
Distribuční funkce: vytvoříme nový datový soubor o 2 proměnných a 8 případech. První proměnnou nazveme X a uložíme do ní hodnoty 0 až 7: do dlouhého jména proměnné napíšeme: $=v0-1$. Druhou proměnnou nazveme DF a uložíme do ní postupně hodnoty $0,\frac{1}{6},\frac{2}{6},\frac{3}{6},\frac{4}{6},\frac{5}{6},1,1$. Grafy - Bodové grafy - Proměnné X a DF - OK - odškrtneme Typ proložení: lineární - OK - 2krát klikneme na pozadí grafu - Spojnice - Obecné - odškrtneme Značky - zaškrtneme Spojnice - Typ čáry - Schod - OK. Opět dvojklikem na pozadí grafu vybereme: Osa - Měříto - Mód:Ručně - Minimum = 0, Maximum = 7 - OK.