20 Skupenské stavy látek
Odlišujeme tři skupenské stavy látek:
|
\(\left.\phantom{\begin{array}1\\2\end{array}}\right\rbrace\) | tekutiny |
|
||
|
||
20.1 Plyny
Plyn je soustava velmi řídce rozptýlených volně pohyblivých částic v prostoru. Pro jejich vlastnosti to má ten důsledek, že plyny jsou schopny velice snadno měnit svůj tvar i objem. Charakteristickou vlastností plynů je tlak, působící rovnoměrně na stěny nádoby. Tlak vzniká nepřetržitým pohybem částic plynu a nárazy částic na stěny nádoby.
Typickou vlastností plynů je, že jejich molekuly jsou daleko od sebe, rychle se pohybují a vzájemně se jen málo ovlivňují. Z toho plyne, že plyn po umístění do jakékoli uzavřené nádoby během pár okamžiků rovnoměrně vyplní celý její objem.
20.1.1 Ideální plyn
Chování látek podléhá velmi mnoha zákonitostem, z nichž ne všechny umíme matematicky popsat a o existenci některých z těchto zákonitostí ani nevíme. Přesto však některé základní rysy chování látek jsou velmi podobné, společné velkým skupinám látek. Podle těchto společných vlastností pak vytváříme tzv. modely, představy o „ideálním“ chování látek. Tak mluvíme o ideálním plynu, ideálním roztoku, ideálním krystalu, apod. Spolu s modelem musíme vždy zvážit, kdy se chování reálně existující látky blíží chování modelu a jestli za daných podmínek můžeme chování látky s přijatelnou přesností předpovídat na základě znalostí vlastností modelu.
Definice ideálního plynu
Ideální plyn v přírodě neexistuje, je to pouze model. Za určitých podmínek se však chování reálných plynů blíží vlastnostem plynu ideálního. Ideální plyn je definován takto:
- Molekuly ideálního plynu mají určitou hmotnost, avšak jejich vlastní objem je nulový (veškerá hmotnost je soustředěna v jednom bodě).
- Mezimolekulové interakční síly (přitažlivé ani odpudivé) v ideálním plynu neexistují.
- Molekuly ideálního plynu se pohybují chaoticky, nezávisle na sobě.
- Ideální plyn nelze zkapalnit.
- Pro ideální plyn zcela přesně platí tzv. stavová rovnice ideálního plynu:
\(\ce{p\ V=n\ R\ T}\tag{20-1}\)
\(\ce{p}\) tlak \(\left(\ce{Pa}\right)\) \(\ce{V}\) objem \(\left(\ce{m^{3}}\right)\) \(\ce{n}\) látkové množství plynu \(\left(\ce{mol}\right)\) \(\ce{R}\) molární plynová konstanta \(\left(\ce{J\,K^{-1}\,mol^{-1}}\right)\) \(\ce{T}\) termodynamická teplota \(\left(\ce{K}\right)\)
Z chování plynů byly vypozorovány dílčí zákonitosti, které byly formulovány postupně během 17.-19. století. Tehdejší pozorování nebyla tak přesná jako dnešní, takže rozdíly mezi reálným a ideálním plynem zanikaly. Zmiňované zákony však platí pouze pro plyn ideální:
- zákon Boyleův-Mariotteův (1660): součin tlaku plynu p a jeho objemu V je pro dané
množství plynu při konstantní teplotě (izotermický děj) konstantní:
\(\left[\mathrm{n, T}\right]\)\(\Rightarrow \mathrm{p\ V=}\) konst.
- zákon Gay-Lussacův (1802) vystihuje lineární závislost objemu na teplotě za konstantního tlaku (izobarický děj):
\(\mathrm{\left[n, p\right]\Rightarrow \dfrac{V}{T}=}\) konst.
- zákon Charlesův (1787) vystihuje lineární závislost tlaku plynu na teplotě při konstantním objemu (izochorický děj):
\(\mathrm{\left[n, V\right]\Rightarrow \dfrac{p}{T}=}\) konst.
- zákon Avogadrův (1811):
Stejné objemy ideálních plynů obsahují za stejné teploty a stejného tlaku stejný počet
molekul.
\(\mathrm{\left[V, T, p\right]\Rightarrow n=}\) konst.
Uvedené zákony vystihují dílčí vztahy proměnných p, V, T (vždy alespoň jedna z uvedených veličin musí být konstantní) pro konstantní množství plynu.
Z Avogadrova zákona vyplývá, že molární objem všech plynů (pokud jejich chování aproximujeme ideálním plynem) je za dané teploty a tlaku stejný. Např.
| \(\mathrm{T}\) | \(\mathrm{p}\) | molární objem ideálního plynu \(\mathrm{V_m}\) je (zaokrouhleno) | |
|---|---|---|---|
| za tzv. normálních podmínek | \(\mathrm{273,15\,K}\) | \(\mathrm{101,325\,kPa}\) | \(\mathrm{22,41\,dm^{3}\,mol^{-1}}\) |
| za tzv. standardních podmínek | \(\mathrm{298,15\,K}\) | \(\mathrm{101,325\,kPa}\) | \(\mathrm{24,47\,dm^{3}\,mol^{-1}}\) |
Pomocí stavové rovnice ideálního plynu lze provést všechny výpočty týkající se stavového chování ideálního plynu. Dílčí zákony (historicky dříve objevené zákonitosti) z ní lze odvodit.
20.1.2 Směsi ideálních plynů
Ve směsi více ideálních plynů se molekuly navzájem neovlivňují, tzn. každý plyn se chová tak, jako by byl ve společném prostoru o objemu V sám.
Pro jednotlivé plyny (označeny indexy i) lze napsat stavovou rovnici ve tvaru:
| \(\mathrm{p_i\ V = n_i\ R\ T}\) | nebo | \(\mathrm{p\ V_i = n_i\ R\ T}\) |
| \(\mathrm{p_i}\)parciální tlak i-tého plynu, tj. tlak, který měl i-tý plyn, kdyby byl ve společném prostoru o objemu V sám | p tlak (celkový tlak plynné směsi) | |
| Vobjem nádoby obsahující uvažovanou směs ideálních plynů | \(\mathrm{V_i}\)parciální objem i-tého plynu, tj. objem, který by i-tý plyn zaujímal za daného tlaku, pokud by byl čistý | |
| \(\mathrm{n_i}\)látkové množství i-tého plynu | \(\mathrm{n_i}\)látkové množství i-tého plynu |
Celkový tlak p směsi ideálních plynů je roven součtu parciálních tlaků všech složek směsi. Tento vztah je znám jako Daltonův zákon (aditivity parciálních tlaků) (1801):
Dáme-li do poměru parciální tlak p i a celkový stav soustavy p (obojí vyjádřeno pomocí stavové rovnice \(\mathrm{p\ V=n\ R\ T\Rightarrow p=n\dfrac{R\ T}{V}}\), resp \(\mathrm{p_i=n_i\dfrac{R\ T}{V}}\) dostáváme vztah:

Tuto rovnici lze přepsat do tvaru
Analogií pro parciální objemy je vztah označovaný jako Amagatův zákon (parciálních objemů):
Pro parciální objem platí obdobný vztah jako pro parciální tlak:
20.1.3 Reálné plyny
Reálné plyny se chovají podobně jako ideální plyn, některými vlastnostmi se však liší (Tab. 32).
| ideální plyn | reálné plyny | |
|---|---|---|
| Reálné plyny mají molekuly nenulové velikosti. |  |
 |
| Molekuly reálných plynů se vzájemně ovlivňují (přitahují nebo odpuzují) |  |
 |
| Molekuly reálných plynů nevyhovují předpokladu neuspořádaného nezávislého pohybu molekul. |  |
 |
| Všechny reálné plyny lze zkapalnit. | Nezkapalnitelný | Všechny reálné plyny jsou zkapalnitelné po ochlazení pod tzv. kritickou teplotu. |
| Kvantitativní popis stavového chování se liší | Stavová rovnice ideálního plynu (21-1) |
|
Chování reálného plynu můžeme popsat pomocí rovnic platných pro plyn ideální tím lépe, čím více se jeho chování blíží definici ideálního plynu (Tab. 31), tj. tehdy když:
- jeho molekuly jsou co nejmenší: např. \(\ce{He\,(g)}\) je podobnější ideálnímu plynu než \(\ce{C2 H6\,(g)}\)
- molekuly se co nejméně silově ovlivňují; např. \(\ce{H2S\,(g)}\) se chová více jako ideální plyn než \(\ce{H2O\,(g)}\), protože u \(\ce{H2O}\) se více uplatňují přitažlivé síly (vodíkové můstky). Reálný plyn se chová podobně jako ideální, pokud je při nízkém tlaku (jeho molekuly jsou daleko od sebe) a při vysoké teplotě (případné mezimolekulové interakce jsou překonány kinetickou energií molekul)
- předpoklad neuspořádaného zcela chaotického navzájem nezávislého pohybu jednotlivých molekul je splněn za stejných podmínek jako předpoklad 2 a se stejným zdůvodněním
- podmínce nezkapalnitelnosti nelze u reálných plynů vyhovět. Některé plyny však mají velmi nízkou kritickou teplotu (např. \(\ce{He}\)), zkapalňují se proto obtížně. Chování takových plynů se blíží ideálnímu chování více než chování látek s vysokou kritickou teplotou (např. vodní pára).
- stavová rovnice ideálního plynu tím lépe popisuje stavové chování reálného plynu, čím lépe jsou splněny předpoklady 1-3.
Zákony pro ideální plyn (kdysi přibližně odpozorované a nyní pro zjednodušení používané) nepopisují reálné chování plynů dostatečně přesně. Nejmenší odchylky reálného chování od ideálního nastávají, pokud reálný plyn má malé špatně polarizovatelné molekuly neschopné tvorby vodíkových můstků a má nízký tlak a vysokou teplotu. V ostatních případech se vyskytují odchylky v chování reálných plynů od ideálního plynu.
Pro popis chování reálných plynů nepostačuje s uspokojivou přesností stavová rovnice ideálního plynu. Používají se složitější vztahy, z nichž nejznámější je van der Waalsova rovnice:
| \(\ce{p}\) | tlak |
| \(\ce{a,b}\) | tabelované koeficienty; a charakterizuje mezimolekulové interakce, b má význam vlastního molárního objemu molekul |
| \(\ce{V_{m}}\) | molární objem plynu |
20.1.4 Zkapalňování plynů a kritický stav
Zkapalňování plynů se týká pouze plynů reálných. Provádíme-li při dostatečně nízké teplotě (Obr. 20-1, oblast 2) stlačování neboli kompresi plynů, dojde při určitém tlaku k vytvoření kapalné fáze. Při další kompresi za konstantního tlaku (Obr. 20-1, oblast 3) se postupně zkapalňují další podíly plynu, až plynná fáze úplně vymizí. Další snižování objemu vzniklé kapalné fáze je možné jen za cenu vysokých tlaků (Obr. 20-1, oblast 4). Nad tzv. kritickou teplotou (Obr. 20-1, oblast 1) plyn není možno zkapalnit sebevětším tlakem.
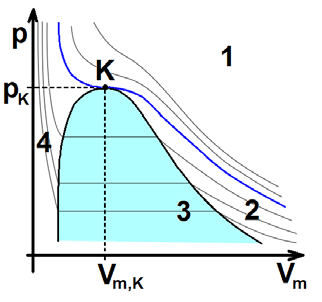
1 – oblast nad kritickou teplotou (plyn nelze pouhým stlačením zkapalnit),
2 – oblast pod kritickou teplotou (plyn lze zkapalnit pouhým stlačením,
3 – oblast koexistence kapaliny a páry,
4 – oblast kapaliny.
Tenké čáry jsou izotermy. Tlusté čáry včetně tmavomodré jsou hranice oblastí 1 – 4.
\(\ce{K}\) – kritický bod
\(\ce{P}\) – tlak
\(\ce{p_{k}}\) – kritický tlak – tlak potřebný při kritické teplotě ke zkapalnění plynu
\(\ce{V_{m}}\) – molární objem
\(\ce{V_{m, k}}\) – kritický molární objem (objem 1 mol látky při kritické teplotě a kritickém tlaku)
Ne vždy bylo známo, že k tomu, aby bylo možno plyn zkapalnit, je nutno jej ochladit na teplotu nižší než je teplota kritická. Navíc některé plyny mají kritickou teplotu velmi nízkou (např. \(\MR{\ce{N2}\!:\ -146,9\ ^{\circ}C;\ \ce{CO}\!:\ -140,1\ ^{\circ}C;\ \ce{Ne}\!:\ -228,75\ ^{\circ}C;\ \ce{H2}\!:\ - 239,91\ ^{\circ}C}\), apod.). Tak nízké teploty nebylo možno dříve dosáhnout. Proto neexistoval žádný způsob, jak uvedené plyny zkapalnit. Proto bývaly plyny s velmi nízkou kritickou teplotou nazývány permanentní (= „věčné“) plyny.
20.2 Kapaliny
Charakteristickou vlastností kapalin je, že jejich molekuly jsou poměrně stěsnané při zachování volné pohyblivosti. To způsobuje, že objem kapalin je velmi málo závislý na tlaku, ale tvar kapaliny se přizpůsobuje tvaru nádoby.
20.2.1 Tenze páry
Z povrchu kapalin i pevných látek se vždy (při libovolné teplotě i tlaku) uvolňují ve větším či menším množství molekuly, které přecházejí do plynné fáze. Parciální tlak této plynné fáze v uzavřeném prostoru nad povrchem kondenzované fáze (kapaliny nebo pevné látky) nazýváme tenze páry.
Rovnováha mezi kondenzovanou fází a její párou je dynamická. To znamená, že molekuly dané látky průběžně přecházejí z kondenzované fáze do plynné a naopak. Při rovnováze v daném časovém intervalu zkondenzuje z páry stejné množství molekul, jaké se z kapaliny vypaří nebo z pevné látky vysublimuje.
Se vzrůstající teplotou tenze páry roste. Při určité teplotě dosáhne tenze páry vnějšího tlaku a v případě rovnováhy kapalina-plyn začne kapalina vřít. Teplota, při níž dosáhne tenze par nad kapalinou vnějšího tlaku, se nazývá teplota varu.
20.2.2 Povrchové napětí kapalin
Kapaliny se chovají tak, jako by jejich povrch byl pokryt tenkou pružnou vrstvou, která se snaží stáhnout povrch kapaliny na co nejmenší velikost. Odborně řečeno, v povrchu kapaliny je napětí, tzv. povrchové napětí. Ideálním tvarem kapalné látky je proto koule, protože při daném objemu má nejmenší povrch. Ke zvětšení povrchu kapaliny je potřeba dodat energii.
20.2.3 Viskozita kapalin
Viskozita je důsledkem smykových napětí v reálné kapalině. Někdy se označuje jako vnitřní tření v kapalině. Pohybující se kapalinu si můžeme představit složenou z vrstviček, které se vůči sobě pohybují. Vrstvičky přiléhající ke stěnám nádoby jsou v klidu, vrstvičky uvnitř nádoby se pohybují nejrychleji. Mezi pohybujícími se vrstvami předpokládáme třecí síly, které způsobují viskozitu kapaliny.
Velmi jednoduše můžeme viskozitu zavést i takto:
- viskozita je míra neochoty tekutiny téci – např. med má větší neochotu téci než voda (odborně říkáme, že med má větší viskozitu než voda)
- viskozita je míra odporu, který tekutina klade pohybujícím se tělesům – např. utíkámeli ve vodě, je náš pohyb pomalejší a namáhavější, než kdybychom utíkali ve vzduchu (z toho plyne, že viskozita vody je větší než viskozita vzduchu)
Závislost viskozity na teplotě
Viskozita kapalin s rostoucí teplotou klesá (toto známe např. u medu nebo vosku – pokud se zahřejí, tečou rychleji), u plynů naopak roste.
20.3 Pevné látky, krystalová struktura
V pevném skupenství jsou atomy, ionty a molekuly rozmístěny tak, že vytvářejí pravidelnou krystalovou mřížku. Zahříváme-li pevnou látku, vzrůstá intenzita pohybu částic v krystalické struktuře. Při dostatečném zahřátí se zrychlí pohyb částic natolik, že jejich kinetická energie převládne nad energií vazebnou a tím se naruší krystalická struktura. To se projeví změnou skupenství z pevného na kapalné. Tento děj se nazývá tání. Během tání stejně jako během každé skupenské přeměny se teplota soustavy nemění.
Teplota, při které je za daného vnějšího tlaku pevná látka a její kapalná fáze v rovnováze, se nazývá teplota tání.
Některé látky mohou přímo přecházet do plynného skupenství bez předcházejícího tání. Tato skupenská přeměna se nazývá sublimace. Je možná jen při nižších tlacích, než je tlak odpovídající trojnému bodu dané látky. Výrazně se projevuje u takových látek, jejichž nasycené páry dosahují už pod trojným bodem (kap. 20.4.2) tlaku, který se rovná atmosférickému tlaku. Typicky sublimující látka je \(\ce{CO2}\) (teplota trojného bodu \(\mathrm{-57\,^{\circ}C}\), tlak trojného bodu \(\mathrm{518\,kPa}\)).
Ve skupenství pevném jsou molekuly či atomy fixovány na pevné polohy (kolem kterých atomy, ionty, resp. atomové či iontové skupiny kmitají). Z toho vyplývají takové vlastnosti pevných látek jako stálost tvaru a objemu, mechanická pevnost a velká hustota.
Mohou nastat dva případy:
- Uspořádání molekul nebo atomů je pravidelné. V tomto případě jde o krystalické látky. Vznikají při pomalém ochlazování kapalné fáze.
- Pevné látky bez pravidelné struktury nazýváme amorfní látky. Jejich struktura se podobá struktuře kapalin, v kterých ustal tepelný pohyb molekul. Proto se amorfní látky někdy považují za podchlazené kapaliny s velmi vysokou viskozitou. Mohou vzniknout např. při rychlém ochlazení kapalné fáze pod tzv. teplotu skelného přechodu.
Příkladem látky, která může existovat jako krystal nebo jako látka amorfní, je uhlík (krystalická forma = diamant nebo grafit, amorfní forma = saze) nebo \(\ce{SiO2}\) (krystalická forma = křemen, amorfní forma – křemenné sklo).
Přechod mezi pevnými a kapalnými látkami tvoří tzv. tekuté (kapalné) krystaly. Jsou to látky mající charakter kapaliny (např. viskozitu – tečou), ale jeví dvojlom a je u nich prokázána určitá vnitřní struktura.
- Tekuté krystaly tvoří nejčastěji sloučeniny s výrazně nesymetrickými molekulami. Molekuly tyčinkovitého tvaru se seskupují paralelně do vrstev tvořících dobře definované roviny. Roviny po sobě dobře kloužou, což se projevuje tokem. Jde o uspořádání smektické (Obr. 20-2a).
- Nemají-li tyčinkovité molekuly bočné interakce, nevytvářejí vrstvy, ale orientace molekul zůstává zachována; tvoří větší svazky, které se mohou podélně pohybovat. V tomto případě jde o uspořádání nematické (Obr. 20-2b).

a – smektické, b – nematické.
20.3.1 Krystalografie
Představa o vnitřní stavbě pevných látek vznikla na základě studia krystalů.
Uspořádáním vnějších krystalových ploch se zabývá krystalografie. Podle symetrie můžeme krystaly rozdělit do sedmi krystalografických soustav:
Polymorfie je schopnost látek (prvků i sloučenin) existovat v různých krystalických modifikacích (soustavách). Polymorfie prvků se nazývá alotropie.
Příkladem polymorfie sloučenin je \(\ce{CaCO3}\) (aragonit, kalcit) a \(\ce{ZnS}\) (sfalerit, wurtzit).
Příkladem polymorfie prvků neboli alotropie je síra (modifikace \(\alpha\)-kosočtverečná nebo \(\beta\)-jednoklonná) nebo uhlík (diamant – krychlová, grafit – šesterečná).
Směsné krystaly
Izomorfie – ionty, atomy nebo molekuly některých látek, které tvoří krystaly stejného typu, se mohou ve svých krystalech zastupovat. Vznikají přitom tzv. směsné krystaly.
Podmínky vzniku směsných krystalů
- stejný typ krystalové mřížky a soustavy pro obě látky, např. krychlová soustava, stejný počet molekul hydrátové vody apod.
- stejný charakter vazby, např. iontová
- blízké objemy zastupujících se částic
Vzdálenost krystalových rovin
Pro stanovení polohy atomů v krystalu (kromě vodíku) se využívá tzv. rentgenová strukturní analýza. Základem matematického zpracování experimentálních dat získaných touto metodou je tzv. Braggova rovnice. Pomocí ní lze určit vzdálenost krystalových rovin.
Dopadá-li svazek rovnoběžných paprsků rentgenového záření na krystalovou rovinu, nastává po jejich odrazu od krystalové roviny interferenční maximum tehdy, je-li:
| \(\ce{d}\) | mřížková konstanta, tj. vzdálenost krystalových rovin \(\left(\ce{m}\right)\) |
| \(\ce{\Theta}\) | úhel, který svírají dopadající paprsky s krystalovou plochou, na niž dopadají \(\left(\ce{^{\circ}}\right)\) |
| \(\ce{n}\) | řád maxima (přirozené číslo) |
| \(\ce{\lambda}\) | vlnová délka rentgenového záření \(\left(\ce{m}\right)\) |
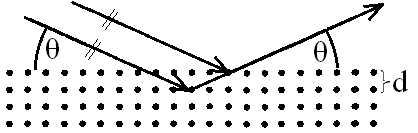
Mezirovinná vzdálenost může záviset na orientaci rovin (Obr. 20-4).

20.3.2 Elementární (základní) buňka
Elementární (základní) krystalová buňka je seskupení částic tvořících základní a jednoduchou stavební jednotku krystalu, jejímž pravidelným opakováním v prostoru vzniká krystal.
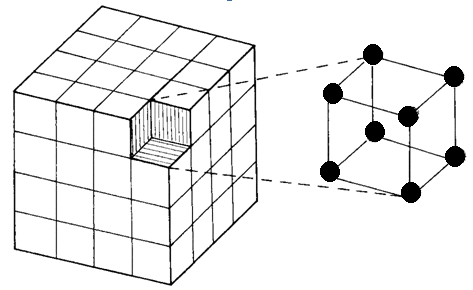
Místo, kde je těžiště atomu, iontu nebo molekuly v elementární buňce, se nazývá klíčový bod. Podle výskytu atomů nebo atomových skupin v klíčových bodech odlišujeme 4 elementární buňky: prostá (osazeny pouze vrcholy buňky), tělesně centrovaná (osazeny vrcholy a střed buňky), plošně centrovaná (osazeny vrcholy buňky a středy jejích stěn) a bazálně centrovaná (osazeny vrcholy buňky a středy její dolní a horní podstavy). V jednotlivých krystalografických soustavách se však vyskytují jen některé z nich. Celkem je 14 možností uspořádání (Tab. 34).
| krystalografická soustava | existující elementární buňka | |||
|---|---|---|---|---|
| prostá | tělesně centrovaná | plošně centrovaná | bazálně centrovaná | |
| krychlová |  |
 |
 |
|
| šesterečná |  |
|||
| klencová |  |
|||
| čtverečná |  |
 |
||
| kosočtverečná |  |
 |
 |
 |
| jednoklonná |  |
 |
||
| trojklonná |  |
|||
20.3.3 Typy krystalů pevných látek
Iontové krystaly
V klíčových bodech elementární buňky jsou ionty. Mezi ionty působí všesměrové elektrostatické síly a díky nim drží iontové krystaly pohromadě. Příkladem iontového krystalu je \(\ce{NaCl}\) – v klíčových bodech se nachází \(\ce{Na^{+}}\) a \(\ce{Cl-}\).

Příkladem iontového krystalu s víceatomovými anionty je \(\ce{BaSO4}\). V klíčových bodech jsou ionty \(\ce{Ba^{2+}}\) a \(\ce{SO_4^{2-}}\).
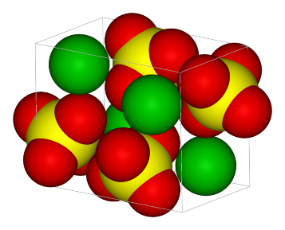
Význam barev: zelená: \(\ce{Ba^{2+}}\), žlutá a červená: \(\ce{SO_4^{2-}}\).
Zastoupení iontů v mřížce musí odpovídat zastoupení iontů ve stechiometrickém vzorci sloučeniny. Vázané ionty (kationty \(\times\) anionty) mají různé poloměry, proto při znázorňování krystalové struktury malé ionty umisťujeme do mezer mezi dotýkající se větší ionty. O typu elementární buňky rozhodne poměr poloměrů \(\ce{r1 : r2}\).
| poměr poloměrů | uspořádání | znázornění |
|---|---|---|
| \(\leq 0,155\) | lineární |  |
| \(0,155 - 0,255\) | trojúhelníkové |  |
| \(0,255 - 0,414\) | tetraedrické |  |
| \(0,414 - 0,732\) | čtvercové |  |
| oktaedrické |  |
|
| \(0,732 - 1,000\) | krychlové |  |
Molekulové krystaly
V klíčových bodech buňky jsou celé molekuly. Ty jsou k sobě v krystalu poutány pomocí vodíkových můstků a slabých vazebných interakcí. Příkladem látek, které v pevné fázi tvoří molekulové krystaly, jsou voda, methan nebo jod.

Červená: atomy kyslíku, bílá: atomy vodíku, čárkovaně jsou vyznačeny vodíkové můstky.
Převzato z: http://en.wikipedia.org/wiki/Molecular_solid a upraveno.

Šedě znázorněny celé molekuly, černobíle rozkreslena jedna molekula \(\ce{CH4}\).
Atomové krystaly
V klíčových bodech buňky jsou atomy. Jde o zesíťované makromolekuly, ve kterých jsou jednotlivé atomy vázány kovalentními vazbami. Vyznačují se vysokou teplotou tání, velkou tvrdostí a pevností. Atomové krystaly tvoří např. uhlík ve formě diamantu.

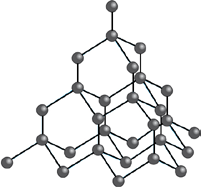
Vlevo základní buňka (černými vazbami zvýrazněna čtveřice sousedících atomů), vpravo opakování tetraedru v mřížce.
Krystaly s kovovou vazbou
V klíčových bodech elementární buňky jsou kationty kovu, mezi nimiž se relativně volně pohybují valenční elektrony všech atomů kovu. Volná pohyblivost těchto elektronů způsobuje velmi dobrou elektrickou vodivost kovů.
Krystalové mřížky kovů tvoří atomy s delokalizovanými vazbami. Atomy jsou stejné, mají tvar koule a snaží se uspořádat co nejtěsněji k sobě. Nejtěsnější uspořádání je hexagonální, vrstvy se skládají nad sebe. Jsou tři možnosti uspořádání:
| elementární buňka | vyplnění prostoru |
|---|---|
| šesterečná | 75 % |
| krychlová plošně centrovaná | 75 % |
| krychlová tělesně centrovaná | 68 % |

a – krychlová tělesně centrovaná, b – krychlová plošně centrovaná, c – šesterečná.
20.3.4 Krystalické mřížky kovalentních látek
- molekulové krystaly
U kovalentních látek o obsazení elementární buňky nerozhodují pouze rozměry atomů, ale především tvar molekul. V krystalické mřížce tak mohou vzniknout dutiny (např. u hlinitokřemičitanů, u kterých je v dutině hlinitokřemičitanové mřížky zachycena tzv. zeolitická voda). V klíčových bodech elementární buňky jsou těžiště molekul. Molekuly jsou pohromadě drženy vodíkovými můstky nebo slabými vazebnými interakcemi. Molekulové krystaly mají nízkou teplotu tání a těkavost.
- atomové krystaly
Klíčové body elementární buňky jsou obsazeny atomy, mezi nimi jsou kovalentní vazby. Tyto krystaly jsou obrovské makromolekuly s lokalizovanými vazbami konkrétně umístěnými mezi atomy. Atomové krystaly jsou extrémně tvrdé, mají vysoké teploty tání (řádově \(\mathrm{1\,000\,^{\circ}C}\)), jsou nerozpustné ve vodě a nevedou elektrický proud.
- vrstevnaté krystaly
Ve vrstvě krystalů jsou atomy drženy kovalentními vazbami (vazby velmi pevné), mezi vrstvami působí van der Waalsovy síly (vazba velmi slabá). Vrstevnaté krystaly jsou podél vrstev štípatelné a otírají se. Příkladem vrstevnatých krystalů je grafit a kyselina boritá.
 Obr. 20-12: Krystalová struktura grafitu.
Obr. 20-12: Krystalová struktura grafitu.
Šedými plochami jsou vyznačeny vrstvy atomů vázaných kovalentními vazbami. - klathráty
Klathráty vznikají tím, že v dutině krystalu je zachycena cizí molekula nebo atom, mají stechiometrické složení. Při rozpouštění nebo roztavení je struktura klathrátu zrušena.
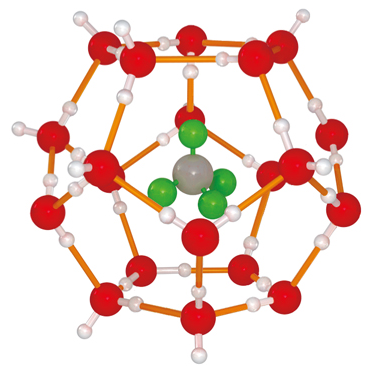 Obr. 20-13: Příklad klathrátu.
Obr. 20-13: Příklad klathrátu.
Upraveno dle http://eng.thesaurus.rusnano.com/wiki/article951. -
interkalátové (vmezeřené) sloučeniny
Interkalátové sloučeniny mohou existovat i v roztoku. Příklady interkalace jsou:
-
komplex DNA-ethydiumbromid používaný k detekci DNA v molekulární biologii
 Obr. 20-14: Reakce schématicky znázorněného řetězce DNA a ethydiumbromidu.
Obr. 20-14: Reakce schématicky znázorněného řetězce DNA a ethydiumbromidu.
Ethydiumbromid se vmezeřuje (interkaluje) mezi páry bází DNA. grafit + atomy alkalických kovů (\(\ce{K}\), \(\ce{Rb}\), \(\ce{Cs}\)) – tyto krystaly jsou různě zbarvené. Pozor, barevná náplň pastelek je tvořená zcela jinými materiály. Příkladem mohou být látky: \(\ce{C8M}\) (červená), \(\ce{C24M}\) (modrá), \(\ce{C64Na}\) (fialová). Písmeno \(\ce{C}\) značí atomy uhlíku, \(\ce{M}\) značí atom některého z uvedených alkalických kovů)
 Obr. 20-15: Schématické znázornění vmezeření atomů alkalických kovů mezi vrstvy grafitu.
Obr. 20-15: Schématické znázornění vmezeření atomů alkalických kovů mezi vrstvy grafitu.
Atomy alkalického kovu jsou znázorněny černě, atomy uhlíku šedě. -
20.3.5 Krystalová voda
Mnoho solí krystalizuje z vodných roztoků v podobě dobře definovaných hydrátů. Jiné pevné fáze však mají proměnlivé množství vody a přechod mezi molekulami vody a jinými složkami krystalu je téměř plynulý. Můžeme rozlišit pět mezních typů interakcí, jejichž hranice nejsou přesně definované, a mnoho sloučenin lze přiřadit k více než jednomu typu.
- \(\ce{\bf H2O}\) koordinovaná v koordinačním kationtu - nejobvyklejší skupina, většinou jde o malé kationty s nábojovým číslem +2 nebo +3 s velkou koordinační schopností. Příkladem jsou komplexy \(\ce{[Be(H2O)4]SO4, [Mg(H2O)6]Cl2, [Ni(H2O)6](NO3)2}\) ad..
- \(\ce{\bf H2O}\) koordinovaná pomocí vodíkové vazby k oxoaniontům - jde o poměrně
neobvyklý způsob, vyskytuje se však u \(\ce{CuSO4\cdot 5H2O}\). Jedna z molekul vody v modré
skalici je vázána pevněji než zbývající čtyři. Každý měďnatý kation v modré skalici je
koordinován čtyřmi molekulami vody a dvěma síranovými skupinami v poloze trans.
Pátá molekula vody je namísto k \(\ce{Cu^{2}+}\) vázána ke dvěma síranovým skupinám a dvěma
dalším molekulám vody (Obr. 20-16).
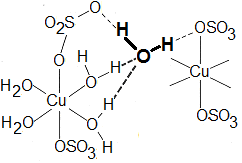 Obr. 20-16: Dva způsoby vazby vody v \(\ce{CuSO4\cdot 5H2O}\).
Obr. 20-16: Dva způsoby vazby vody v \(\ce{CuSO4\cdot 5H2O}\).
Zvýrazněna je ta molekula vody, která je vázána jinak než zbývající čtyři molekuly vody. - mřížková voda - pomocí hydratace kationtu nebo aniontu může dojít k vyrovnání rozdílů ve velikosti jednotek obsazující mřížkové polohy, takto vytvořené dutiny v mřížce mohou být zaplněny vodou. Příkladem je \(\ce{KF\cdot 2H2O, NaCl\cdot 2H2O}\) ad.
- zeolitická voda - voda se vyskytuje ve velkých dutinách buňky, nedostatek silných specifických interakcí umožňuje plynule měnit stupeň hydratace, příkladem jsou hlinitokřemičitany
- klathrátové hydráty - \(\left(\ce{H2O}\right)_\mathrm{n}\) může vytvořit různé struktury s velkými dutinami, které v sobě mohou umisťovat hostující molekuly
20.4 Fázové rovnováhy
Fáze je část soustavy, která má v celém svém objemu stejné vlastnosti chemické i fyzikální. Na tvaru a velikosti částic nezáleží. Každá fyzikálně nebo chemicky odlišná, homogenní a mechanicky oddělitelná část soustavy představuje samostatnou fázi.
Jestliže systém tvořený dvěma nebo více fázemi je ve stavu termodynamické rovnováhy, říkáme, že v systému je ustavena fázová rovnováha.
Děj, při kterém přechází (mění se) určité množství látky z jedné fáze do druhé, nazýváme fázový přechod, příp. fázová přeměna. Fázové přechody dělíme na přechody 1. a 2. druhu.
Fázové přechody 1. druhu jsou známé pod označením „skupenské přeměny“.
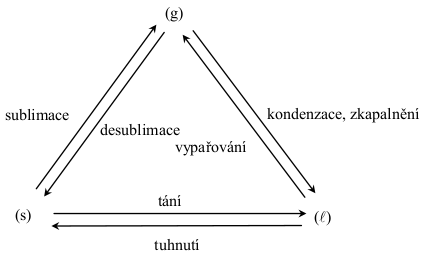
Fázové přeměny 2. druhu jsou:
- \(\ce{C}\)(grafit)\(\ce{<=>C}\)(diamant)
\(\ce{S(\alpha)<=>S(\beta)}\)
\(\ce{Sn}\)(bílý)\(\ce{<=>Sn}\)(šedý) - změna feromagnetických vlastností, např. u \(\ce{Fe}\) při zahřátí na vysokou teplotu
20.4.1 Gibbsův fázový zákon
Gibbsův fázový zákon charakterizuje fázové rovnováhy v heterogenních soustavách. Je znám ve tvaru:
\(\mathrm{v = s -f + 2}\tag{20-8}\)| \(\mathrm{v}\) | počet stupňů volnosti |
| \(\mathrm{s}\) | počet složek |
| \(\mathrm{f}\) | počet fází |
Počet stupňů volnosti je počet intenzivních stavových veličin, které můžeme nezávisle na sobě měnit, aniž by se tím změnil počet fází v soustavě.
Počet složek je minimální počet čistých látek, jimiž lze danou soustavu realizovat. Např. \(\ce{CaO}\) a \(\ce{CO2}\) lze získat rozkladem \(\ce{CaCO3}\). Soustava obsahující pouze \(\ce{1\,mol\,CaO}\) a \(\ce{1\,mol\,CO2}\) tedy obsahuje pouze jednu složku (více též příklady uvedené dále).
Klasifikace soustav podle počtu stupňů volnosti
- invariantní (v = 0),
- univariantní (v = 1),
- bivariantní (v = 2),
- trivariantní (v = 3), atd.
Počet fází viz kapitola Fázové rovnováhy.
Zadání:
Bylo smícháno 1 mol plynného amoniaku, 1 mol plynného chlorovodíku a 4 mol pevného chloridu amonného. Kolik stupňů volnosti má vzniklá soustava?
Dosazujeme:
| \(\mathrm{f = 2}\) | počet fází: jedna fáze pevná a jedna plynná |
| \(\mathrm{s = 1}\) | počet složek soustavy: amoniak a chlorovodík v poměru 1:1 lze připravit z chloridu amonného, jedinou složkou soustavy je tedy chlorid amonný \(\ce{NH4Cl <=> NH3 + HCl}\) |
Dosazením do Gibbsova zákona:
| \begin{align*} \mathrm{v + f} &= \mathrm{s + 2}\\ \mathrm{v + 2} &= 1 + 2\\ \mathrm{v} &= 1 \qquad\Rightarrow \end{align*} | soustava má 1 stupeň volnosti; je univariantní |
Zadání:
Bylo smícháno 1 mol plynného amoniaku, 2 mol plynného chlorovodíku a 4 mol pevného chloridu amonného. Kolik stupňů volnosti má vzniklá soustava?
Dosazujeme:
| \(\mathrm{f = 2}\) | počet fází: jedna fáze pevná a jedna plynná |
| \(\mathrm{s = 2}\) | počet složek soustavy: amoniak a chlorovodík v poměru 1:1 připravíme pouze rozkladem chloridu amonného (další \(\ce{HCl}\) je nutno dodat zvlášť), proto má soustava 2 složky |
Dosazením do Gibbsova zákona:
| \begin{align*} \mathrm{v + f} &= \mathrm{s + 2}\\ \mathrm{v + 2} &= 2 + 2\\ \mathrm{v} &= 2 \qquad\Rightarrow \end{align*} | soustava má 2 stupně volnosti; je bivariantní |
20.4.2 Trojný bod
Pojem trojný bod se používá jen u čistých látek. Trojný bod je kombinace tlaku a teploty, při níž jsou v rovnováze 3 fáze téže látky (nemusí se nutně jednat o 3 skupenství, může jít např. i o 2 fáze pevné a 1 kapalnou apod.).
V jednosložkové soustavě mohou vedle sebe existovat nanejvýš 3 fáze, jak plyne z Gibbsova fázového zákona (kap. 20.4.1). Systém v trojném bodě nemá žádný stupeň volnosti.
| \(\ce{p (Pa)}\) | \(\ce{t (^{\circ}C)}\) | ||
|---|---|---|---|
| voda (platí pro šesterečnou krystalovou strukturu ledu; za extrémních podmínek lze získat i jiné struktury ledu) | \(613,2\) | \(0,0075\) | |
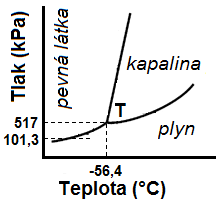
| \(\ce{\bf CO2}\) | \(5 \cdot 10^{5}\) | \(- 56,4\) | |
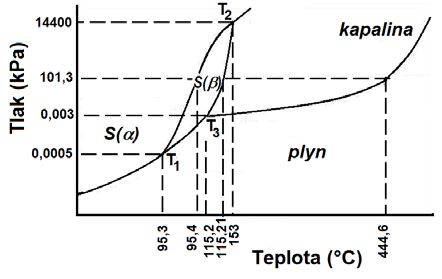
| síra (trojné body \(\ce{T1}\) až \(\ce{T3}\) jsou označeny stejně jako ve fázovém diagramu - Obr. 20-19) | \(\ce{(T1)}\) | \(1,8\) | \(95,6\) |
| \(\ce{(T2)}\) | \(1,4 \cdot 10^{8}\) | \(153,7\) | |
| \(\ce{(T3)}\) | \(3,73\) | \(119\) |
20.4.3 Fázové diagramy
Pod pojmem fázový diagram rozumíme graf, z něhož lze určit, v jaké fázi nebo fázích se systém nachází za dané teploty, tlaku a celkového složení systému.
Existují různé typy fázových diagramů. V zásadě je členíme podle počtu složek v systému. Máme pak fázové diagramy pro soustavu jednosložkovou, dvousložkovou a třísložkovou. Pro složitější soustavy nastávají problémy se znázorněním ve dvourozměrném prostoru (papír, obrazovka počítače).
Následující obrázky jsou příklady fázových diagramů. Zatím je důležité zapamatovat si základní tvary fázových diagramů.
Fázové diagramy jednosložkových soustav

Fázové diagramy dvousložkových soustav
Pro úplné znázornění fázového diagramu dvousložkové soustavy by byl potřeba trojrozměrný diagram, neboť dvousložková soustava může mít až tři stupně volnosti:
\[\begin{array}{rcl} \MR{v + f} & = & \MR{s + 2}, \text{v systému musí být aspoň jedna fáze}\\ \MR{v + 1} & = & \MR{2 + 2}\\ \MR{v} & = & \MR{3} \end{array}\]Protože trojrozměrný diagram se na ploše (papír, obrazovka) obtížně znázorňuje, volí zafixuje se obvykle jedna stavová veličina (buď teplota, nebo tlak) konstantní. Tím o jednotku klesne počet stupňů volnosti soustavy. U dvousložkových soustav tedy obvykle pracujeme s fázovým diagramem izobarickým (p = konst.) nebo izotermickým (T = konst.).
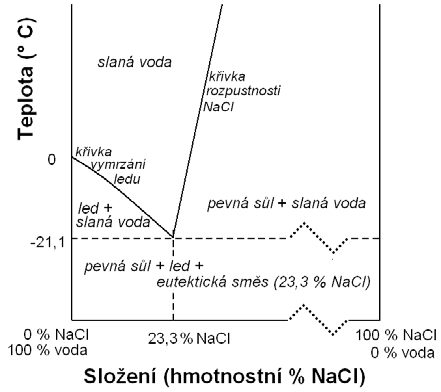
Na vodorovné ose fázového diagramu dvousložkové soustavy bývá obvykle složení. Protože žádné složky nemůže být méně než 0 % a více než 100 % (molární zlomek se pohybuje mezi hodnotami 0 a 1), mají fázové diagramy dvousložkových soustav tvar vaničky (Obr. 20-21 a následující).

a – diagram izotermický,
b – diagram izobarický
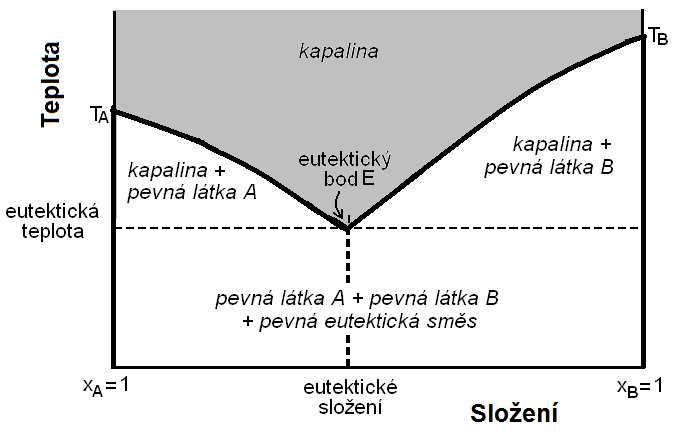
Fázové diagramy třísložkových soustav
Fázový diagram třísložkových soustav může být až čtyřrozměrný, neboť trojsložková soustava může mít až čtyři stupně volnosti:
\[\begin{array}{rcl} \MR{v + f} & = & \MR{s + 2}, \text{v systému musí být aspoň jedna fáze}\\ \MR{v + 1} & = & \MR{3 + 2}\\ \MR{v} & = & \MR{4} \end{array}\]Pro znázornění fázového chování takovýchto soustav se využívá např. tzv. Gibbsův trojúhelník (Obr. 20-24) - znázornění složení soustavy pro danou teplotu a tlak. Na každé jeho straně je vynášen obsah jedné z látek ve směsi. Odečítání z Gibbsova trojúhelníku bude podrobněji vysvětleno v rámci fyzikální chemie.
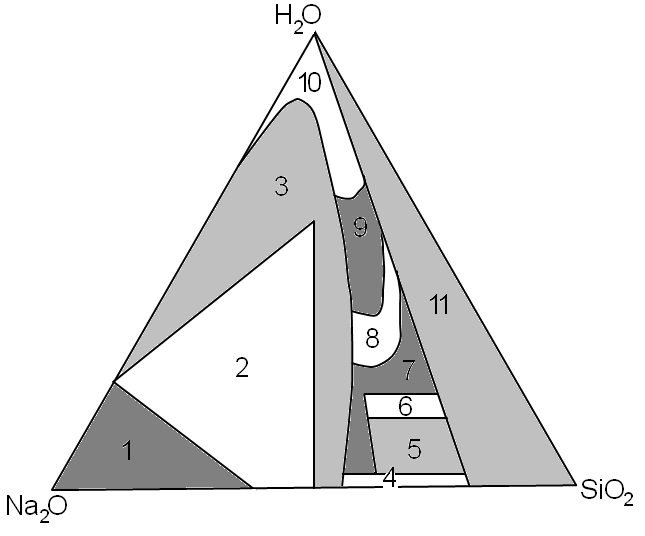
- bezvodý \(\ce{Na4SiO4}\) a jeho zrnité směsi s \(\ce{NaOH}\),
- zrnité krystalické alkalické křemičitany, jako \(\ce{Na2SiO3}\) a jeho hydráty,
- částečně krystalizované směsi,
- skla,
- hydratovaná skla,
- dehydratované kapaliny,
- polotuhé látky a gely,
- nestálé viskózní kapaliny,
- běžné komerční kapaliny,
- zředěné kapaliny,
- nestálé kapaliny a gely










